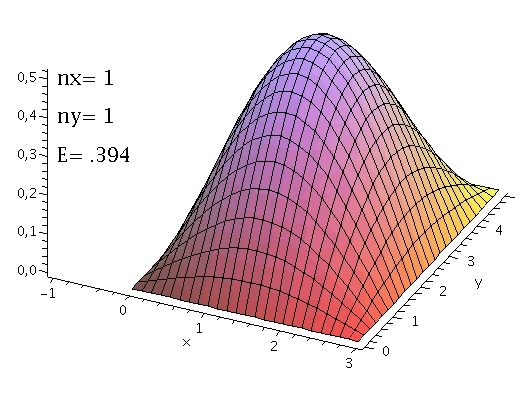Ein Quantenteilchen im eindimensionalen Potentialtopf mit unendlich hohen Wänden
| > | restart:
with(plots): |
Wir betrachten im folgenden einen quantenmechanischen Zustand eines Teilchens, welcher in einem Potentialtopf mit unendlich hohen Wänden gebunden ist und wir beschränken uns zunächst auf eine räumliche Dimension. Der Potentialtopf sei wie folgt definiert: V(x)=0 falls x=[0,a] und unendlich für x<0 und x>a. Da der Hamiltonoperator dieses Systems nicht von der Zeit abhängt, vereinfacht sich die Schrödingergleichung. Die Schrödingergleichung im Inneren des Potentialtopfes (0<= x <= a ) lautet:
| > | SGL:=diff(psi(x),x,x)=-2*m*E/hq^2*psi(x);
SGL:=diff(psi(x),x,x)=-k^2*psi(x): |
| (1.1) |
Da der Potentialtopf an seinen Grenzen unendlich ist, muss die Wellenfunktion im Aussenbereich identisch verschwinden (psi(0)=0 und psi(a)=0). Wir arbeiten die erste Randbedingungen direkt in die allgemeine Lösung der Schrödingergleichung mit ein; sie besitz somit das folgende Aussehen (wobei k^2=2*m*E/hq^2 ):
| > | Loes:=subs({_C1=A},dsolve({SGL,psi(0)=0}));
|
| (1.2) |
Durch die zweite Randbedingungen (psi(a)=0) erhalten wir eine Quantisierungsvorschrift für die Wellenzahl k:
| > | _EnvAllSolutions:=true:
Quantk:=k=solve(subs(x=a,rhs(Loes))=0,k): Quantk:=subs(_Z1=n,Quantk); QuantE:=E=solve(subs({k=sqrt(2*m*E)/hq},Quantk),E); |
| (1.3) |
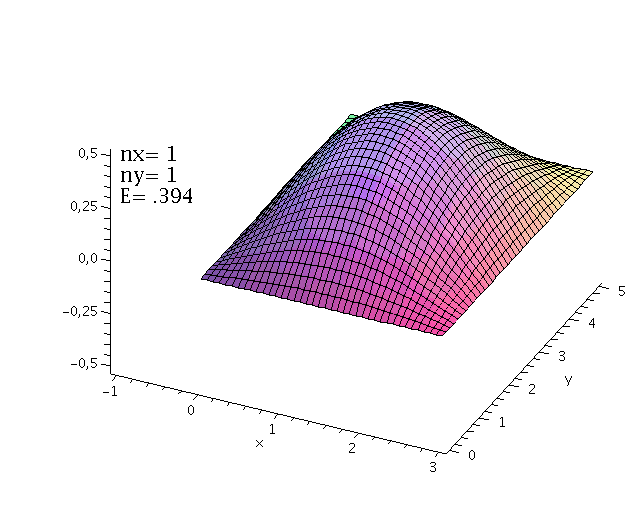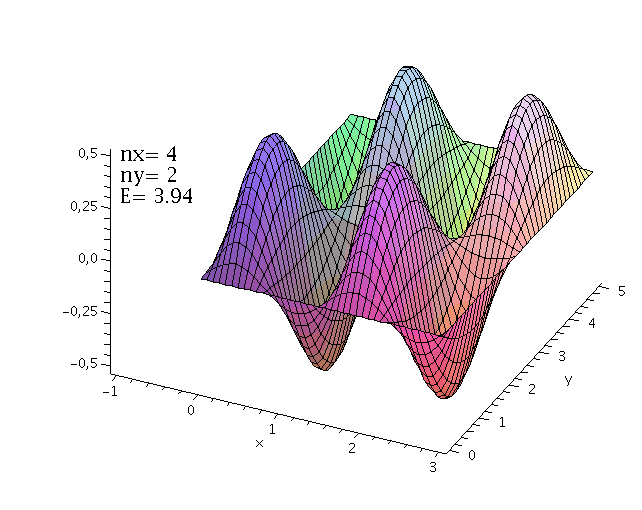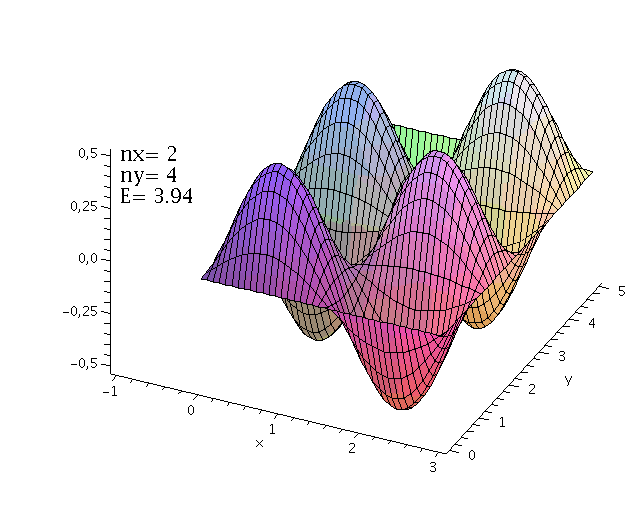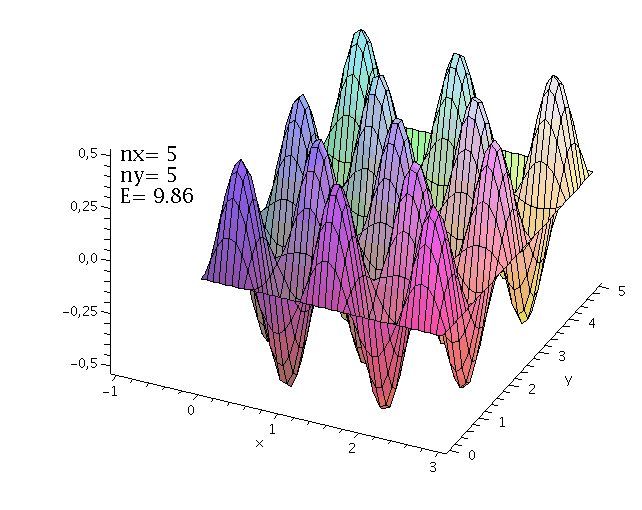
Aufgrund dieser Quantisierungseigenschaft kann die Wellenzahl k und somit auch die Energie E des Quantenteilchens nur diskrete Werte annehmen.Setzen wir im folgenden z.B. hq=m=1, a=3, so können wir die Wellenfunktion und den Energieeigenwert des Quantenteilchens im Grundzustand (n=1) berechnen:
| > | n=1;
k[1]:=subs({n=1,a=3},rhs(Quantk)); E[1]:=subs({n=1,a=3,hq=1,m=1},rhs(QuantE)); psi[1]:=rhs(subs({k=k[1],A=A[1]},Loes)); |
| (1.4) |
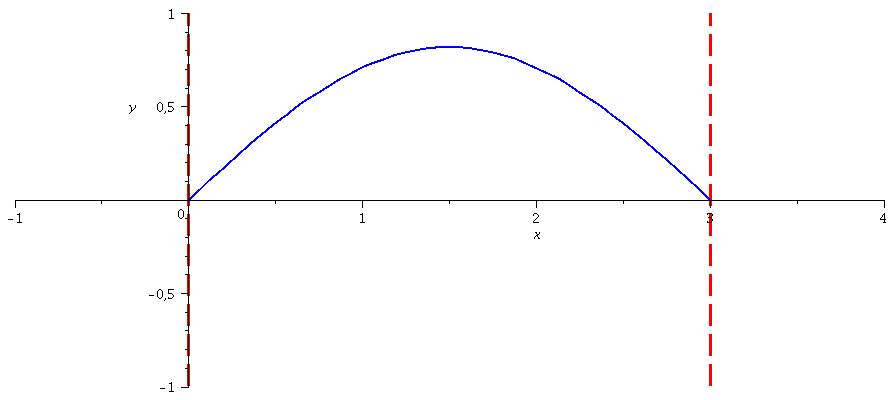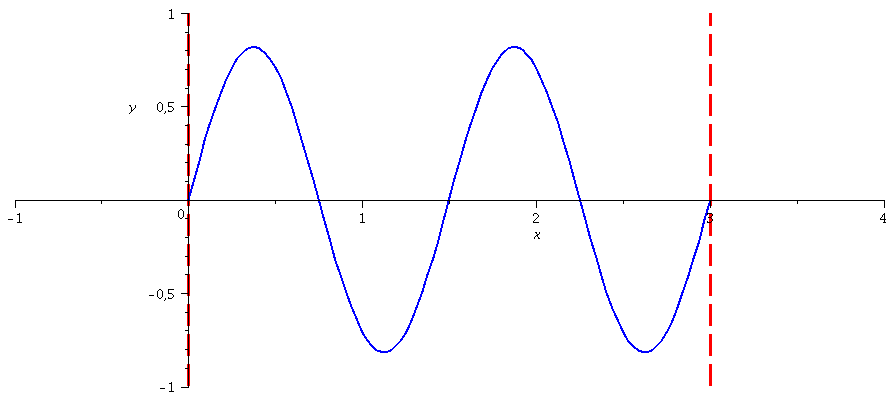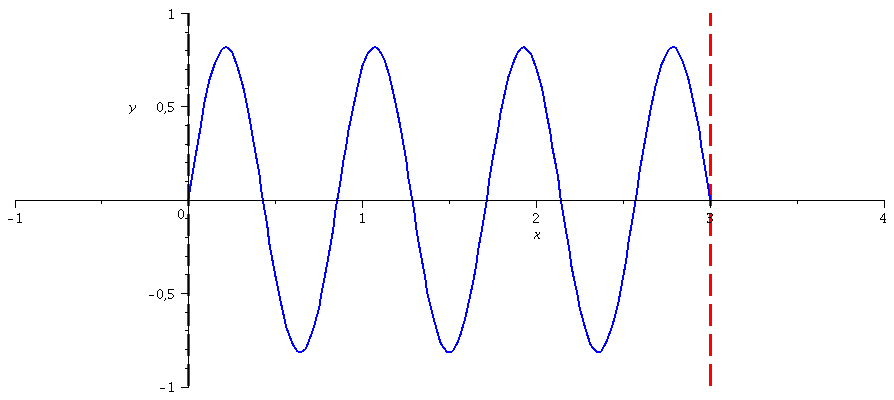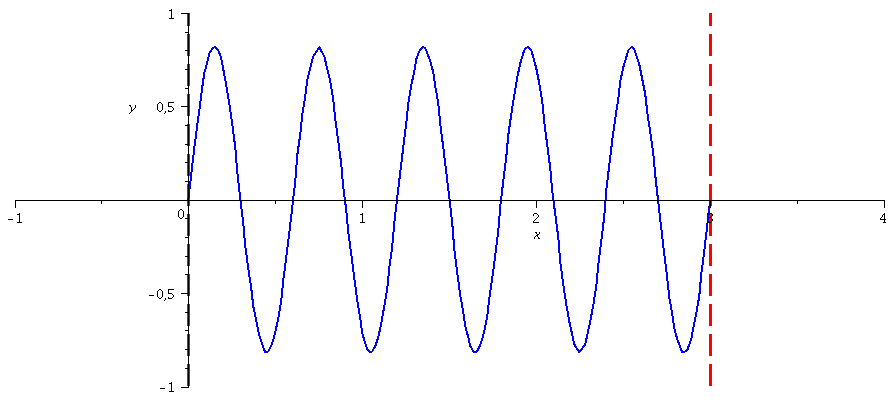
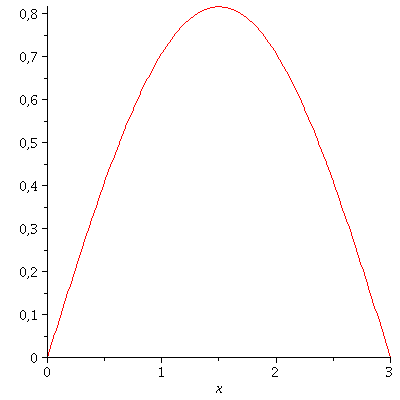
Die noch unbekannte Amplitude lässt sich durch die Normierungsbedingung festlegen. Die Wellenfunktion des Quantenteilchens im Grundzustand besitz somit das folgende Aussehen:
| > | GLNorm:=int(conjugate(psi[1])*psi[1],x=0..3)=1;
A[1]:=solve(subs(conjugate(A[1])=A[1],GLNorm),A[1])[1]; plot(psi[1],x=0..3); |
 |
Die Zustandsfunktionen der höherenergetischen Zustände berechnet man in gleicher Weise (n=1,2,3,4,....):
| > | restart:
with(plots): SGL:=diff(psi(x),x,x)=-k^2*psi(x): Loes:=subs({_C1=A},dsolve({SGL,psi(0)=0})): _EnvAllSolutions:=true: Quantk:=k=solve(subs(x=a,rhs(Loes))=0,k): Quantk:=subs(_Z1=n,Quantk): QuantE:=E=solve(subs({k=sqrt(2*m*E)/hq},Quantk),E): |
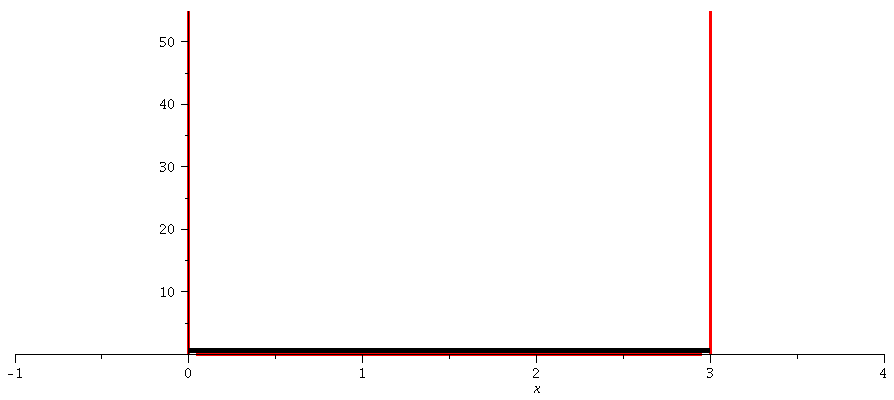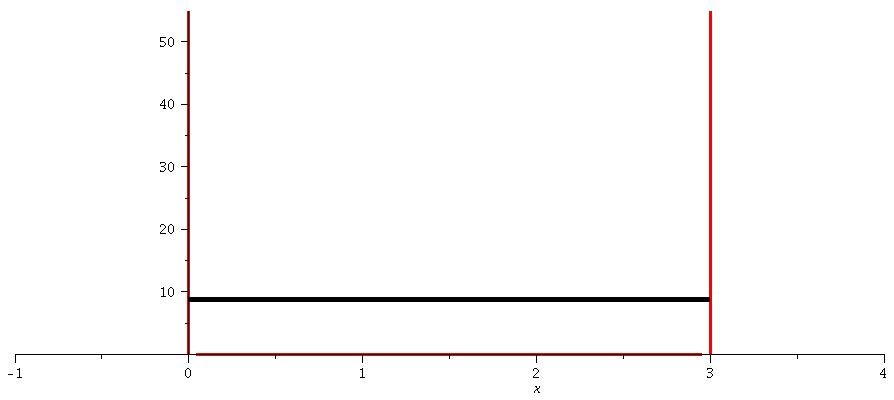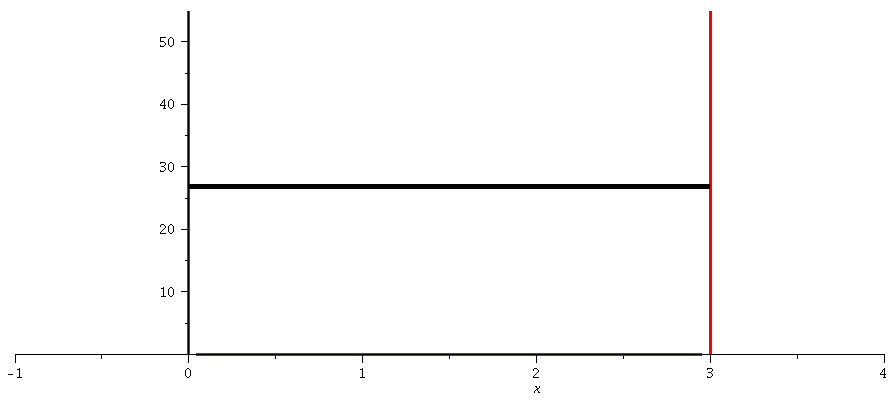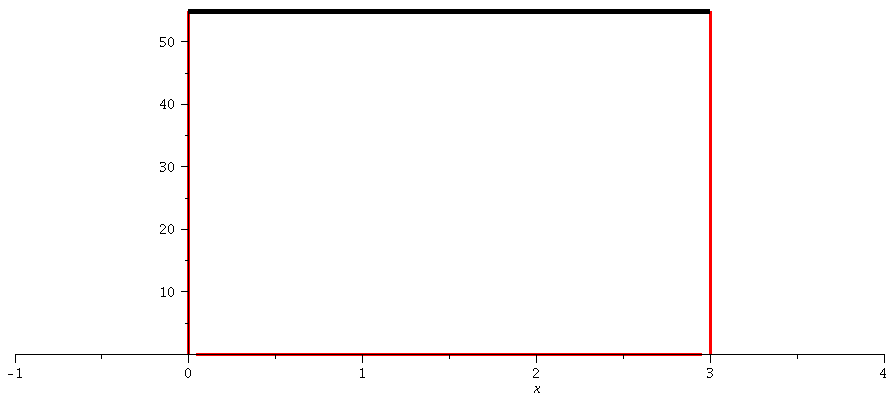
| > | maxn:=10:
maxE:=subs({a=3,hq=1,m=1,n=maxn},rhs(QuantE)): V:=piecewise(0 <= x and x<= a,0, x > a, infinity, x < 0, infinity): GrenzeLinks:=implicitplot(x=0, x=-1..4, y=0..maxE, colour=red, thickness=3): GrenzeRechts:=implicitplot(x=3, x=-1..4, y=0..maxE, colour=red, thickness=3): GrenzeLinks1:=implicitplot(x=0, x=-1..4, y=-1..1, colour=red, linestyle=3, thickness=3): GrenzeRechts1:=implicitplot(x=3, x=-1..4, y=-1..1, colour=red, linestyle=3, thickness=3): PPot:=plot(subs(a=3,V),x=-1..4,thickness=3): PPot:=display(PPot,GrenzeLinks,GrenzeRechts): display(PPot): for n from 1 by 1 to maxn do k[n]:=subs({a=3},rhs(Quantk)); E[n]:=subs({a=3,hq=1,m=1},rhs(QuantE)); psi[n]:=rhs(subs({k=k[n],A=A[n]},Loes)); GLNorm:=int(conjugate(psi[n])*psi[n],x=0..3)=1; A[n]:=solve(subs(conjugate(A[n])=A[n],GLNorm),A[n])[1]; PlotEnergie[n]:=plot(E[n],x=-0..3,thickness=5,color=black): Plotpsi[n]:=plot(psi[n],x=0..3,thickness=2,color=blue): Ani[n]:=display(Matrix(2,1,[display(GrenzeLinks1,GrenzeRechts1,Plotpsi[n],view=[-1..4,-1..1]),display(PPot,PlotEnergie[n])])); od: |
| > | display([seq(Ani[i],i=1..10)],insequence=true);
|
|
| > |