Streuzustände eines Quantenteilchens an einem eindimensionalen Potentialtopf mit endlicher Tiefe 

>	restart: with(plots): with(StringTools):

 

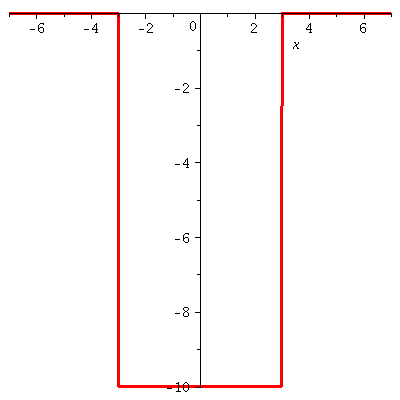
Wir betrachten im folgenden einen quantenmechanischen Zustand eines Teilchens, welcher an einem Potentialtopf streut und wir beschränken uns zunächst auf eine räumliche Dimension. Der Potentialtopf besitz das folgende Aussehen: 

>	V:=piecewise(abs(x) <=a, -V0); seta:=3; setV0:=10; plot(subs({a=seta,V0=setV0},V),x=-7..7,thickness=3);

 

Da der Hamiltonoperator dieses Systems nicht von der Zeit abhängt, vereinfacht sich die Schrödingergleichung. Wir betrachten nun einen nicht gebundenen Zustand des Teichens (E>=0) an drei unterschiedlichen Orten. Die Schrödingergleichung links vom Potentialtopf (x < -3 ) lautet: 

>	SGLLinks:=diff(psi[L](x),x,x)=-2*m*E/hq^2*psi[L](x); SGLLinks:=diff(psi[L](x),x,x)=-kappa^2*psi[L](x):

 

(1.1)

 

Im inneren Bereich lautet sie: 

>	SGLInnen:=diff(psi[M](x),x,x)=-2*m*(E+V0)/hq^2*psi[M](x); SGLInnen:=diff(psi[M](x),x,x)=-k^2*psi[M](x):

 

(1.2)

 

Im äußeren Bereich lautet sie hingegen: 

>	SGLRechts:=diff(psi[R](x),x,x)=-2*m*E/hq^2*psi[R](x); SGLRechts:=diff(psi[R](x),x,x)=-kappa^2*psi[R](x):

 

(1.3)

 

Die Lösung im linken Bereich stellt eine sowohl einlaufende als auch auslaufende (reflektierte) ''de Broglieschen" Materiewelle dar, wohingegen im rechten Bereich (x>a) nur eine auslaufende Welle existiert. Im mittleren Bereich des Potentialtopfes (-a<x<a) sind jedoch beide Lösungen zulässig (wobei kappa=sqrt(2*m*E)/hq und k=sqrt(2*m*(E+V0))/hq) 

>	Loes1:=A*exp(I*kappa*x) +B*exp(-I*kappa*x); Loes2:=C*sin(k*x) + D*cos(k*x); Loes3:=F*exp(I*kappa*x);

 

 

 

	(1.4)

 

An den Grenzbereichen (x=-a und x=a) müssen die Zustandsfunktionen stetig und glatt ineinander übergehen: 

>	Eq1:=eval(subs(x=-a,Loes1))=eval(subs(x=-a,Loes2)); Eq2:=eval(subs(x=-a,diff(Loes1,x))=eval(subs(x=-a,diff(Loes2,x)))); Eq3:=eval(subs(x=a,Loes2))=eval(subs(x=a,Loes3)); Eq4:=eval(subs(x=a,diff(Loes2,x))=eval(subs(x=a,diff(Loes3,x))));

 

 

 

 

	(1.5)

 

Diese vier Gleichungen kann man mittels algebraischer Operationen wie folgt umformen:   

>

EqC:=C=simplify(solve(subs(F=solve(Eq3,F),Eq4),C)); EqF:=F=simplify(solve(subs(C=simplify(solve(subs(F=solve(Eq3,F),Eq4),C)),Eq3),F)); EqA:=A=simplify(expand(subs(C=simplify(solve(subs(F=solve(Eq3,F),Eq4),C)),solve(subs(B=solve(Eq1,B),Eq2),A)))); EqB:=B=simplify(expand(subs(C=simplify(solve(subs(F=solve(Eq3,F),Eq4),C)),solve(subs(A=solve(Eq1,A),Eq2),B))));

 

 

 

 

	(1.6)

 

Die Lösung hängt somit lediglich noch von einer Amplitude ab, die von der Intensität der einlaufenden Welle bestimmt ist. Wir wählen A=1 und setzten zusätzlich m=hq=1, V0=10, E=0.5 und a=3. Die Zustandsfunktion läßt sich dann in den einzelnen Bereichen als eine komplexwertige Funktion von x angeben  

>

seta:=3; setV0:=10; setE:=0.5; setkappa:=subs({m=1,hq=1,E=setE},sqrt(2*m*E)/hq); setk:=subs({m=1,hq=1,E=setE,V0=setV0},sqrt(2*m*(V0+E))/hq); setD:=solve(1=evalf(subs({a=seta,kappa=setkappa,k=setk},rhs(EqA))),D): A=1; B2=Re(conjugate(evalf(subs({a=seta,kappa=setkappa,k=setk,D=setD},rhs(EqB))))*evalf(subs({a=seta,kappa=setkappa,k=setk,D=setD},rhs(EqB)))); C2=Re(conjugate(evalf(subs({a=seta,kappa=setkappa,k=setk,D=setD},rhs(EqC))))*evalf(subs({a=seta,kappa=setkappa,k=setk,D=setD},rhs(EqC)))); D2=Re(conjugate(setD)*setD); F2=Re(conjugate(evalf(subs({a=seta,kappa=setkappa,k=setk,D=setD},rhs(EqF))))*evalf(subs({a=seta,kappa=setkappa,k=setk,D=setD},rhs(EqF)))); Loes1a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({A=rhs(EqA),B=rhs(EqB)},Loes1))); Loes2a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({C=rhs(EqC)},Loes2))); Loes3a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({F=rhs(EqF)},Loes3)));

 

 

 

 

 

 

 

 

 

 

 

 

 

	(1.7)

 

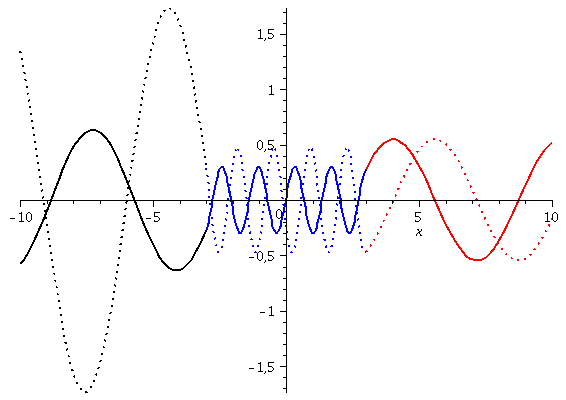
und darstellen (gepunktete Funktion stellt den Imaginärteil dar): 

>

PLL:=plot({Re(Loes1a)},x=-10..-seta,color=black,thickness=2): PLM:=plot({Re(Loes2a)},x=-seta..seta,color=blue,thickness=2): PLR:=plot({Re(Loes3a)},x=seta..10,color=red,thickness=2): PLLIM:=plot({Im(Loes1a)},x=-10..-seta,color=black,thickness=2,linestyle=2): PLMIM:=plot({Im(Loes2a)},x=-seta..seta,color=blue,thickness=2,linestyle=2): PLRIM:=plot({Im(Loes3a)},x=seta..10,color=red,thickness=2,linestyle=2): display(PLL,PLM,PLR,PLLIM,PLMIM,PLRIM);

 

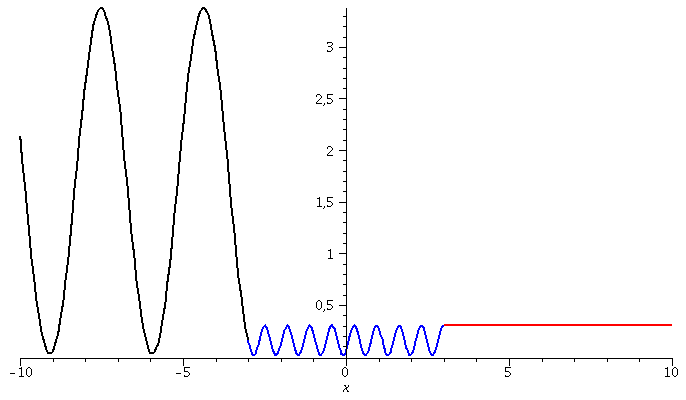
Die Warscheinlichkeitsdichte besitzt das folgende Aussehen: 

>	PLL:=plot({Re(conjugate(Loes1a)*Loes1a)},x=-10..-seta,color=black,thickness=2): PLM:=plot({Re(conjugate(Loes2a)*Loes2a)},x=-seta..seta,color=blue,thickness=2): PLR:=plot({Re(conjugate(Loes3a)*Loes3a)},x=seta..10,color=red,thickness=2): display(PLL,PLM,PLR);

 

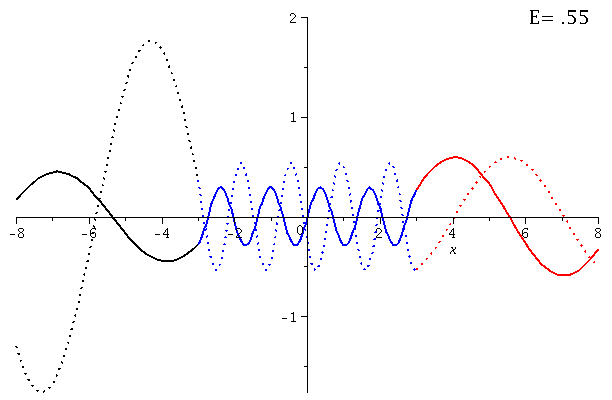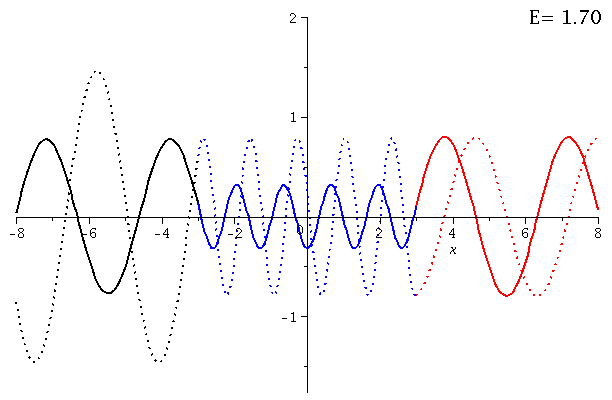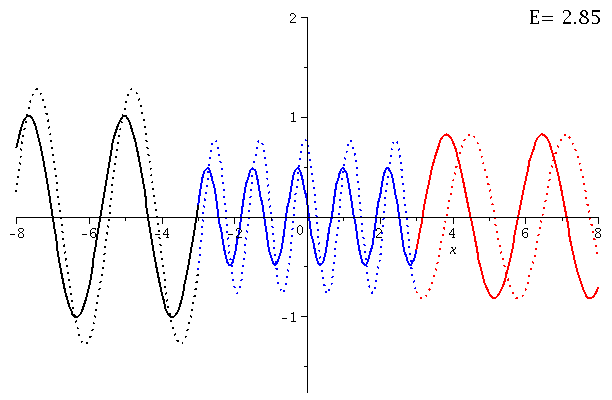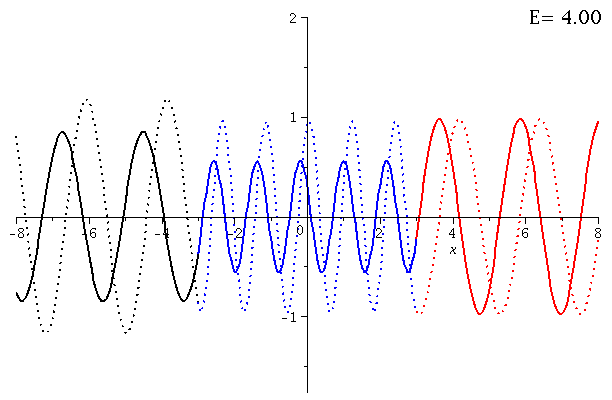
In dieser Animation wird der Real- und Imaginärteil des Zustandes bei variierender Energie der einlaufenden Welle dargestellt (E=[0.55 , 4.00]): 

>

seta:=3; setV0:=10; setkappa:=subs({m=1,hq=1},sqrt(2*m*E)/hq); setk:=subs({m=1,hq=1,V0=setV0},sqrt(2*m*(V0+E))/hq); setD:=solve(1=evalf(subs({a=seta,kappa=setkappa,k=setk},rhs(EqA))),D): Loes1a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({A=rhs(EqA),B=rhs(EqB)},Loes1))); Loes2a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({C=rhs(EqC)},Loes2))); Loes3a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({F=rhs(EqF)},Loes3))); for EE from 1 by 1 to 70 do setE:=0.05*EE + 0.5: Digits := 3: Ptext1:=textplot([6,2, Join(["E=",convert(setE,string)])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]): Digits := 20: PLL:=plot({Re(subs(E=setE,Loes1a))},x=-8..-seta,color=black,thickness=2): PLM:=plot({Re(subs(E=setE,Loes2a))},x=-seta..seta,color=blue,thickness=2): PLR:=plot({Re(subs(E=setE,Loes3a))},x=seta..8,color=red,thickness=2): PLLIM:=plot({Im(subs(E=setE,Loes1a))},x=-8..-seta,color=black,thickness=2,linestyle=2): PLMIM:=plot({Im(subs(E=setE,Loes2a))},x=-seta..seta,color=blue,thickness=2,linestyle=2): PLRIM:=plot({Im(subs(E=setE,Loes3a))},x=seta..8,color=red,thickness=2,linestyle=2): Ani[EE]:=display(PLL,PLM,PLR,PLLIM,PLMIM,PLRIM,Ptext1); od:

 

 

 

 

 

 

 

	(1.8)

 

>	display([seq(Ani[i],i=1..70)],insequence=true);

 

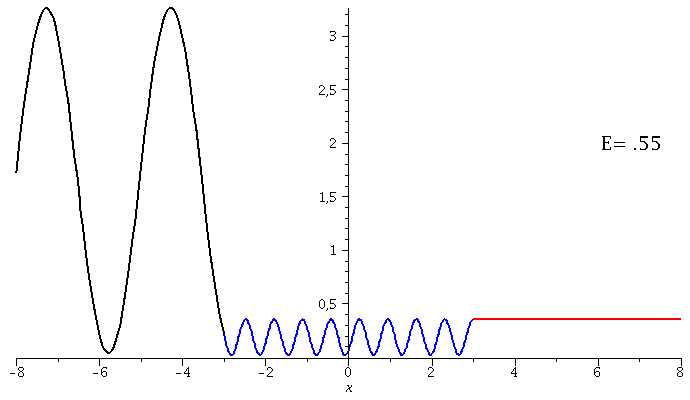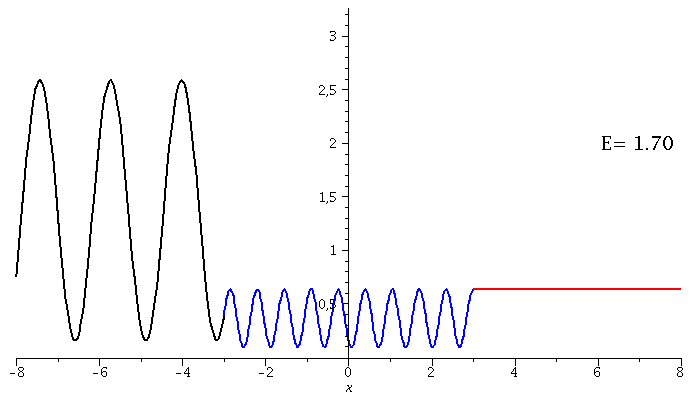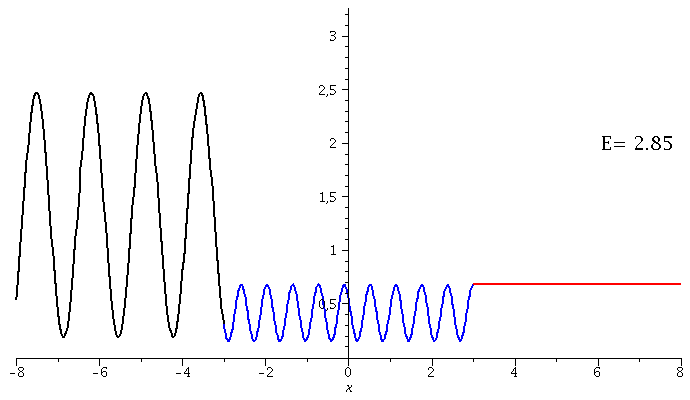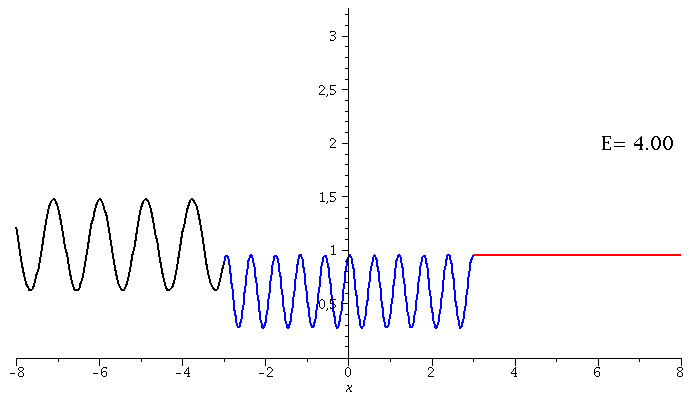
In dieser Animation wird der Warscheinlichkeitsdichte bei variierender Energie der einlaufenden Welle dargestellt: 

>

seta:=3: setV0:=10: setkappa:=subs({m=1,hq=1},sqrt(2*m*E)/hq): setk:=subs({m=1,hq=1,V0=setV0},sqrt(2*m*(V0+E))/hq): setD:=solve(1=evalf(subs({a=seta,kappa=setkappa,k=setk},rhs(EqA))),D): Loes1a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({A=rhs(EqA),B=rhs(EqB)},Loes1))): Loes2a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({C=rhs(EqC)},Loes2))): Loes3a:=evalf(subs({a=seta,D=setD,kappa=setkappa,k=setk},subs({F=rhs(EqF)},Loes3))): for EE from 1 by 1 to 70 do setE:=0.05*EE + 0.5: Digits := 3: Ptext1:=textplot([6,2, Join(["E=",convert(setE,string)])], align =RIGHT,color=black,font = [TIMES, ROMAN, 15]): Digits := 20: PLL:=plot({conjugate(subs(E=setE,Loes1a))*subs(E=setE,Loes1a)},x=-8..-seta,color=black,thickness=2): PLM:=plot({conjugate(subs(E=setE,Loes2a))*subs(E=setE,Loes2a)},x=-seta..seta,color=blue,thickness=2): PLR:=plot({conjugate(subs(E=setE,Loes3a))*subs(E=setE,Loes3a)},x=seta..8,color=red,thickness=2): Ani[EE]:=display(PLL,PLM,PLR,Ptext1); od:

 

>	display([seq(Ani[i],i=1..70)],insequence=true);

 

Der Transmissionskoeffizient T ergibt sich durch T=F^2/A^2 und der Reflexionskoeffizient R durch R=B^2/A^2. Stellt man diese beiden Größen als Funktion der Energie der einlaufenden Welle dar ergibt sich der folgende funktionale Zusammenhang (a=3, T:rot und R:blau). Analytisch ergibt sich der folgende Ausdruck für den Transmissionskoeffizienten: 

>	Tanalytisch:=1/(1+(V0^2*(sin(2*a*sqrt(2*m*(E+V0)))/hbar)^2)/(4*E*(E+V0))); TT:=simplify(simplify(conjugate(rhs(EqF))*rhs(EqF))/simplify(conjugate(rhs(EqA))*rhs(EqA))): RR:=simplify(simplify(conjugate(rhs(EqB))*rhs(EqB))/simplify(conjugate(rhs(EqA))*rhs(EqA))):

 

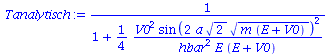(1.9)

 

>

seta:=3; setD:=1; setV0:=10; setkappa:=subs({m=1,hq=1},sqrt(2*m*E)/hq); setk:=subs({m=1,hq=1,V0=setV0},sqrt(2*m*(V0+E))/hq); Tanaly:=subs({hbar=1,m=1,hq=1,V0=setV0,a=seta},Tanalytisch); T:=Re(subs({a=seta,D=setD,kappa=setkappa,k=setk},TT)): R:=subs({a=seta,D=setD,kappa=setkappa,k=setk},RR): PLT:=plot(T,E=0..10,color=red,thickness=2): PLR:=plot(R,E=0..10,color=blue,thickness=2): PLTAnaly:=plot(Tanaly,E=0..10,color=black,thickness=2,linestyle=2): display(PLT,PLR,PLTAnaly,view=0..1.1);

 

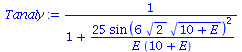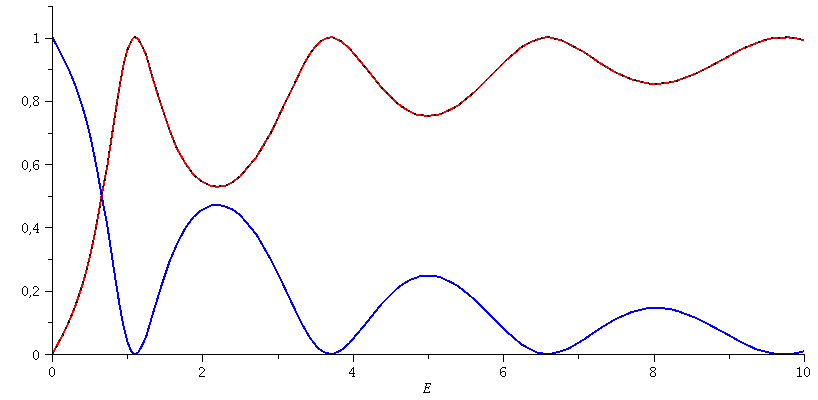Der Transmissionskoeffizient ist gleich 1 falls die Energie die folgenden Werte annimmt: 

>	fsolve(subs(hbar=1,m=1,hq=1,V0=setV0,a=seta,Tanalytisch)=1,E=1..2); fsolve(subs(hbar=1,m=1,hq=1,V0=setV0,a=seta,Tanalytisch)=1,E=3..4); fsolve(subs(hbar=1,m=1,hq=1,V0=setV0,a=seta,Tanalytisch)=1,E=6..7); fsolve(subs(hbar=1,m=1,hq=1,V0=setV0,a=seta,Tanalytisch)=1,E=9..11);

 

 

 

 

	(1.10)

 

Diese Werte entsprechen den ungebundenen Energie-Eigenwerte im unendlichen Potentialtopf (n=9, ..12) 

>	En:=n^2*Pi^2*hq^2/(2*m*(2*a)^2)-V0; evalf(subs({n=8,m=1,hq=1,V0=setV0,a=3},En)); evalf(subs({n=9,m=1,hq=1,V0=setV0,a=3},En)); evalf(subs({n=10,m=1,hq=1,V0=setV0,a=3},En)); evalf(subs({n=11,m=1,hq=1,V0=setV0,a=3},En)); evalf(subs({n=12,m=1,hq=1,V0=setV0,a=3},En));

 

 

 

 

 

 

	(1.11)

 

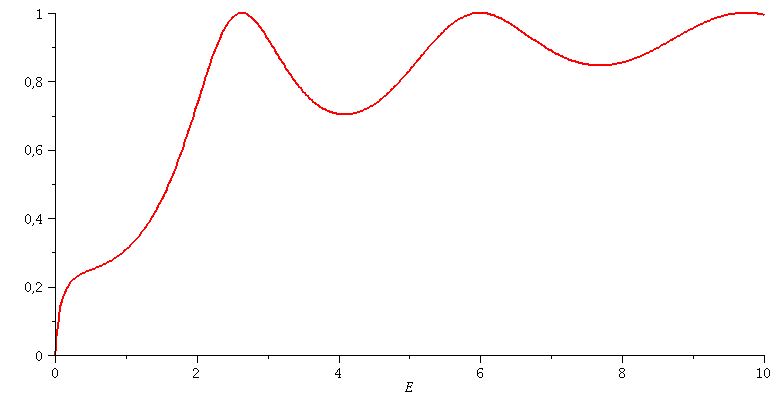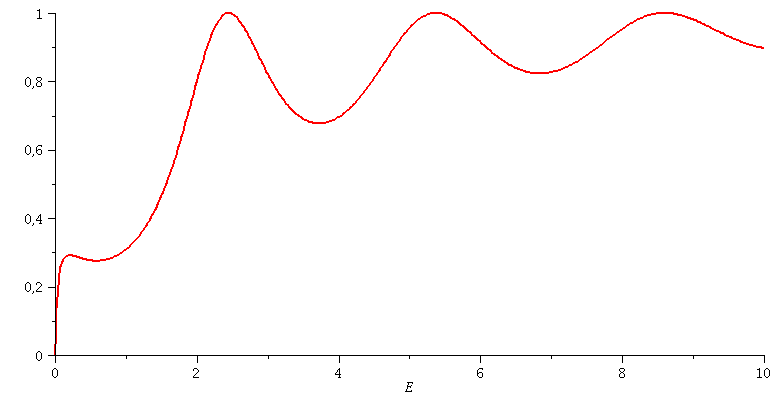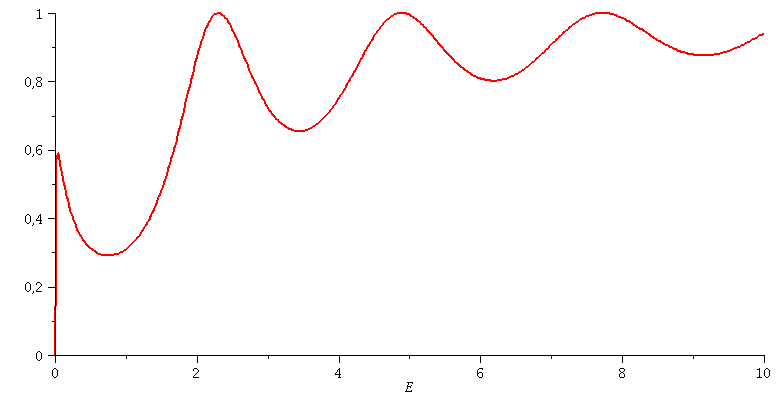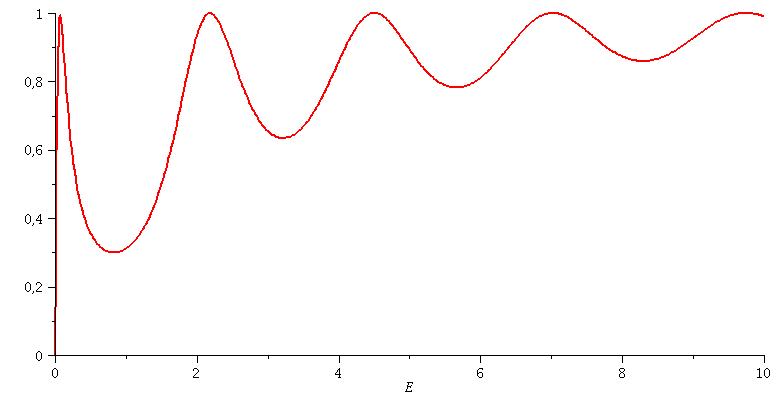
Transmissionskoeffizient: Animation der Breite des Topfes a=[2.5 , 3.5]  

>	animate(subs(hbar=1,m=1,hq=1,V0=setV0,Tanalytisch),E=0..10,a=2.5..3.5,color=red,thickness=2,numpoints=500);

 

Transmissionskoeffizient: Animation der Tiefe des Topfes V0=[7 , 12]  

>	animate(subs(hbar=1,m=1,hq=1,a=3,Tanalytisch),E=0..10,V0=7..12,color=red,thickness=2,numpoints=500);

 

>
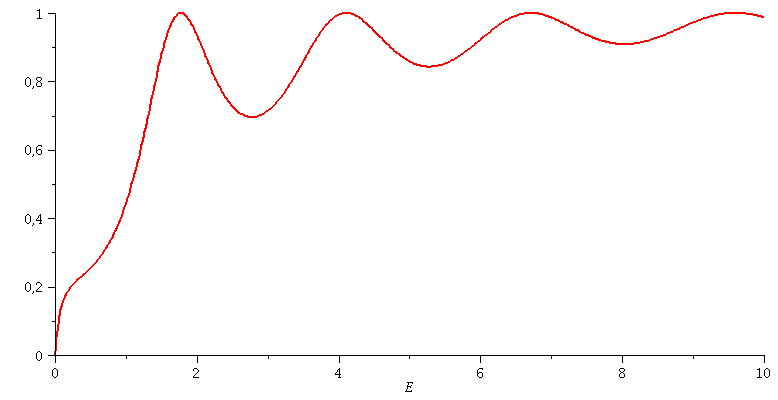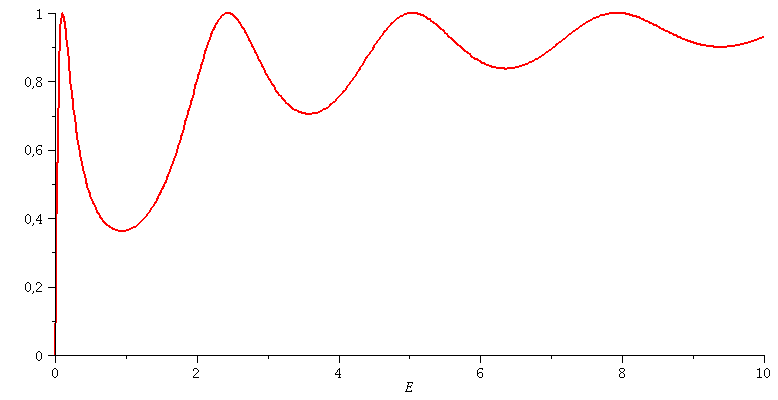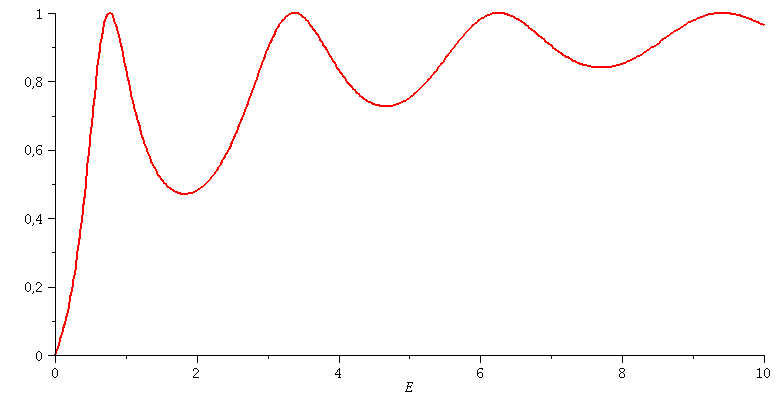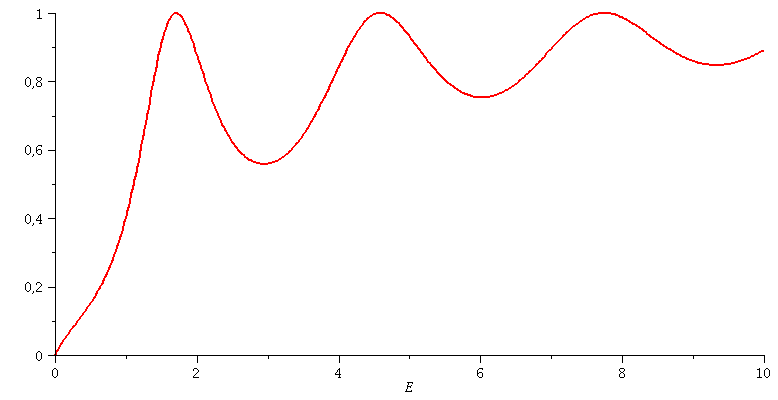