Einführung 

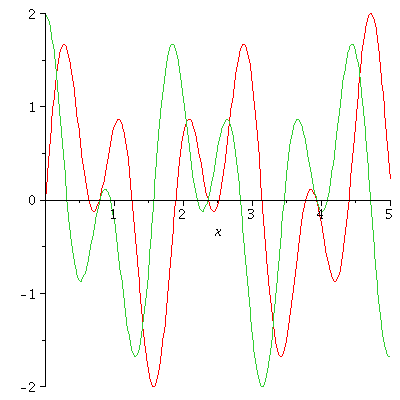
Die Fourier-Reihe 

>	restart: with(plots): with(plottools):

 

Fourier: Jede periodische Funktion f(x), die beschränkt und stückweise stetig ist, lässt sich als eine Linearkombination von Sinus- und Cosinusfunktionen darstellen und in eine Fourier-Reihe entwickeln. 

>	a:=(x0,l,n)->1/l*int(f(x)*cos(n*Pi*x/l),x=x0..x0+2*l); b:=(x0,l,n)->1/l*int(f(x)*sin(n*Pi*x/l),x=x0..x0+2*l); g:=(x0,l,N)->a(x0,l,0)/2+sum((a(x0,l,n)*cos(n*Pi*x/l)+b(x0,l,n)*sin(n*Pi*x/l)),n=1..N);

 

 

 

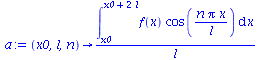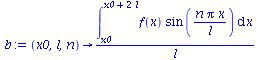	(2.1)

 

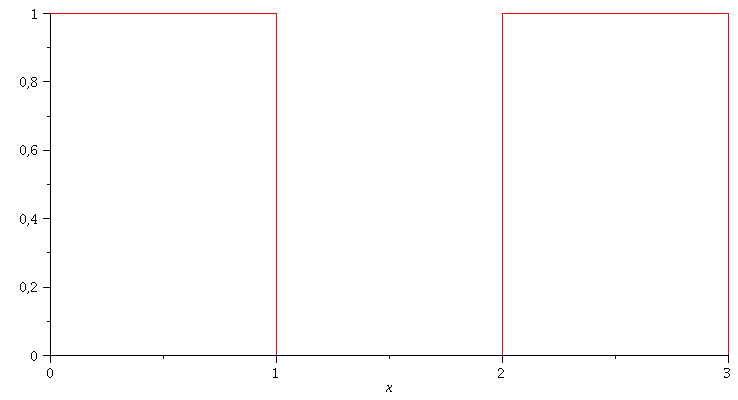
Beispiel 1: Periodische Folge von Rechteckpulsen 

>	f:=x->piecewise(x<1,1,x<2,0,x<3,1): plot(f(x),x=0..3);

 

Fourier-Reihe mit drei Gliedern (N=3): 

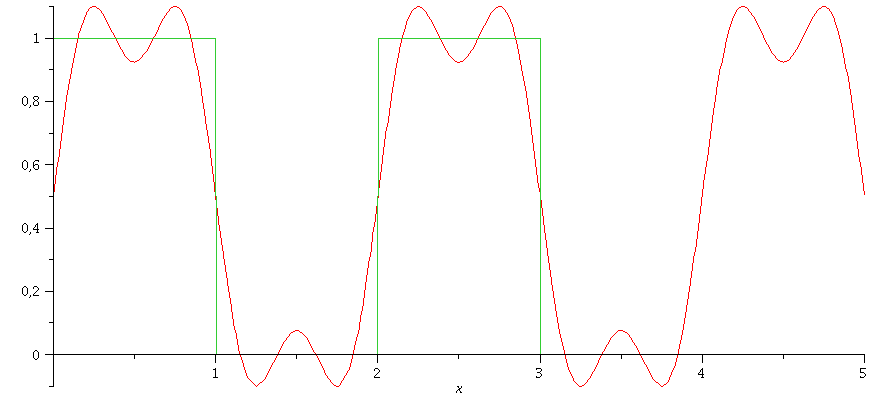
>	g(0,1,3); plot({f(x),g(0,1,3)},x=0..5);

 

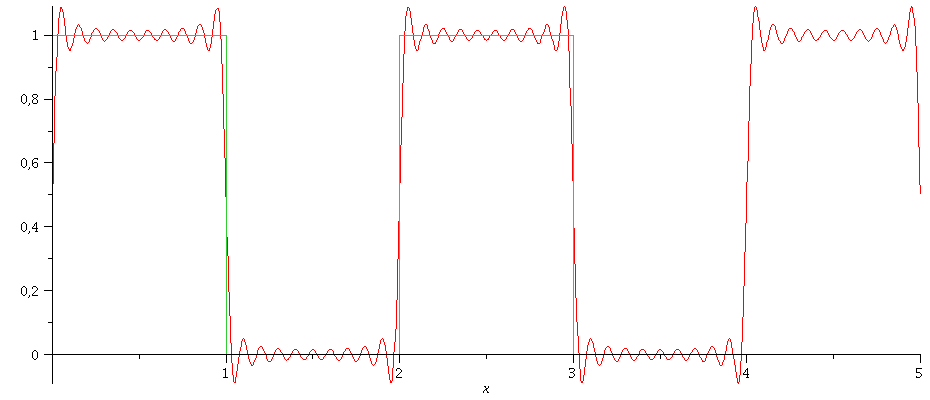
Fourier-Reihe mit 20 Gliedern (N=20): 

>	g(0,1,20); plot({f(x),g(0,1,20)},x=0..5,numpoints=200);

 

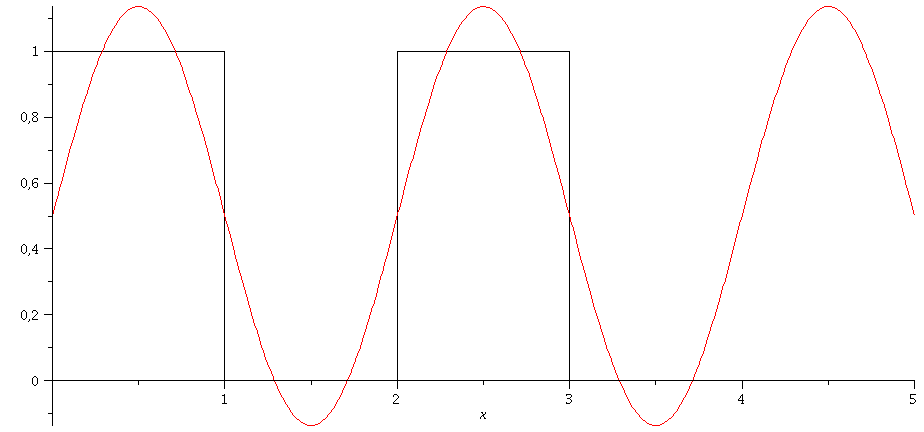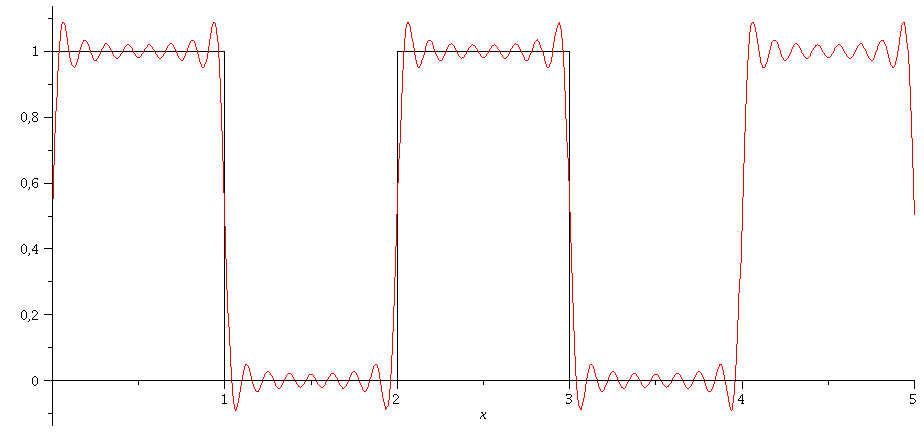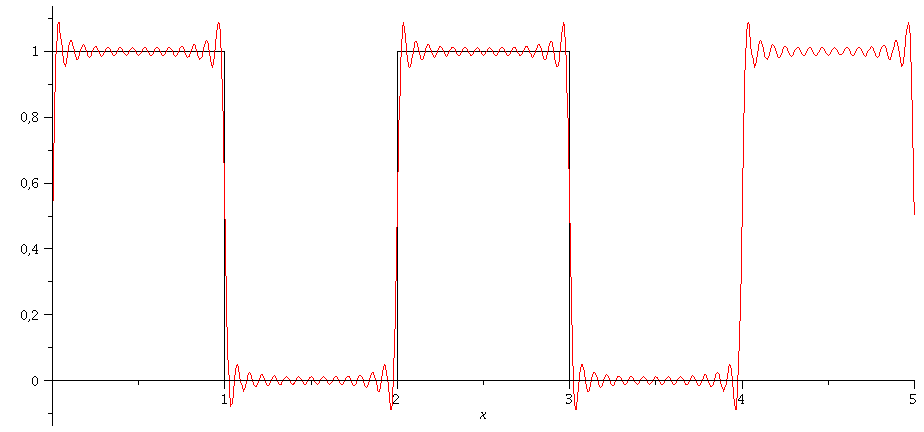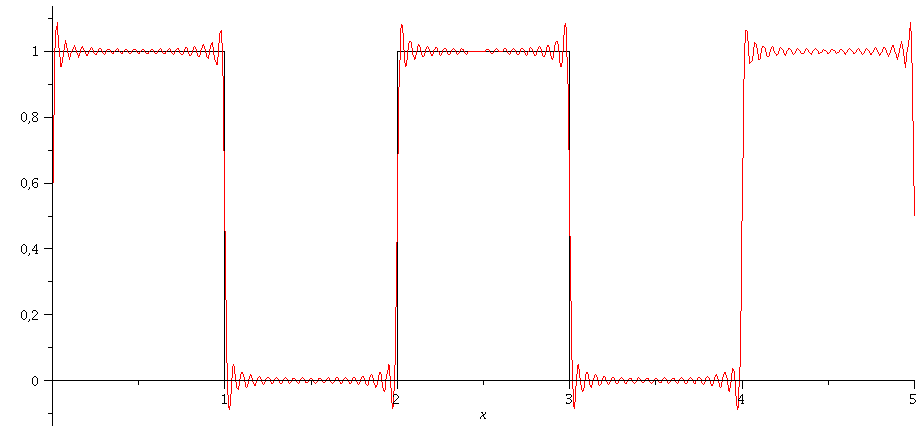
Animation: N=2 bis N=40: 

>	ff:=plot(f(x),x=0..5,numpoints=200,color=black): Nend:=40: for i from 2 by 1 to Nend do NN:=i; gg:=plot(g(0,1,NN),x=0..5,numpoints=200,color=red); Ani[i]:=display(ff,gg); od:

 

>	display([seq(Ani[i],i=2..Nend)],insequence=true);

 

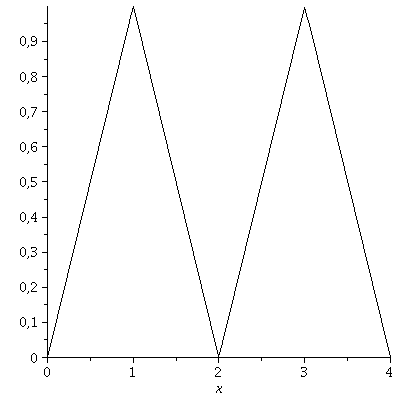
Beispiel 2: Dreieckskurve 

>	f:=x->piecewise(x<1,x,x<2,-x+2,x<3,x-2,x<4,-x+4): plot(f(x),x=0..4,color=black);

 

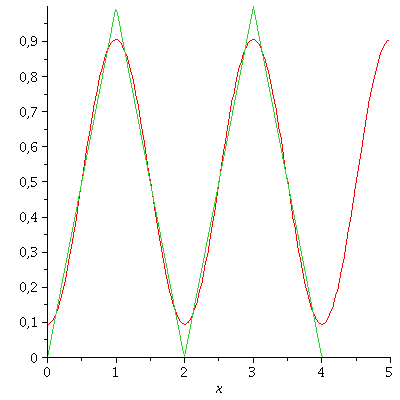
Fourier-Reihe mit drei Gliedern (N=2): 

>	g(0,1,2); plot({f(x),g(0,1,2)},x=0..5);

 

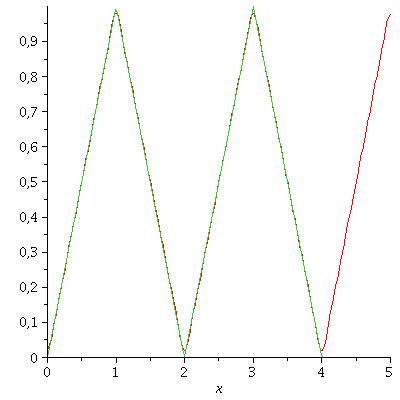
Fourier-Reihe mit drei Gliedern (N=10): 

>	g(0,1,10); plot({f(x),g(0,1,10)},x=0..5);

 

>

 

Fouriertransformation einer Zustandsfunktion 

Wir betrachten eine Zustandsfunktion psi die aus einer Superposition von zwei de Brogliesche Materiewellen besteht (Achtung nicht normiert!) und stellen den Real- und Imaginärteil dar: 

>	psi:=x->exp(I*3*x) + exp(I*7*x); plot({Re(psi(x)),Im(psi(x))},x=0..5);

 

Die Fouriertransformierte setzt sich aus zwei Diracschen Deltafunktionen zusammen, da nur zwei k-Werte vorliegen: 

>	with(inttrans): FourPsi:=1/sqrt(2*Pi)*fourier(psi(x),x,k);

 

(3.1)