Marcus Kasner
Institut für Theoretische Physik

WS2024
Aktuelle Vorlesung ab 18. Oktober 2024
Einführung in die Hydrodynamik
Die Renormierungsgruppe in der Physik
SS2024

Pfadintegrale in der Quantenmechanik
und in der Statistischen Physik
SS2022
WS2018/19
WS2014/15
SS2011
SS2009

Die Quanten-Hall-Effekte
WS2019/20
WS2013/14
SS2007

Exakt lösbare Modelle in der Vielteilchenphysik
WS2020/21
SS2017
WS2012/13
WS2009/10

Theorie der Anderson-Lokalisierung
SS2023
WS2017/18
SS2013
WS2008/09

Fortgeschrittene Themen der
Theorie der Supraleitung und Suprafluidität
WS2022/23
SS2019
SS2014

Theorie der Supraleitung
WS2016/17
WS2011/12
WS2007/08

Starke Magnetfelder in der Festkörperphysik
SS2021
SS2016
WS2010/11

Mathematische Ergänzungen zur Vorlesung
Theoretische Physik I
WS2015/16

Quantentheorie des Magnetismus
SS2012

Musterbildung
SS2008

Physics Department

University of Frankfurt

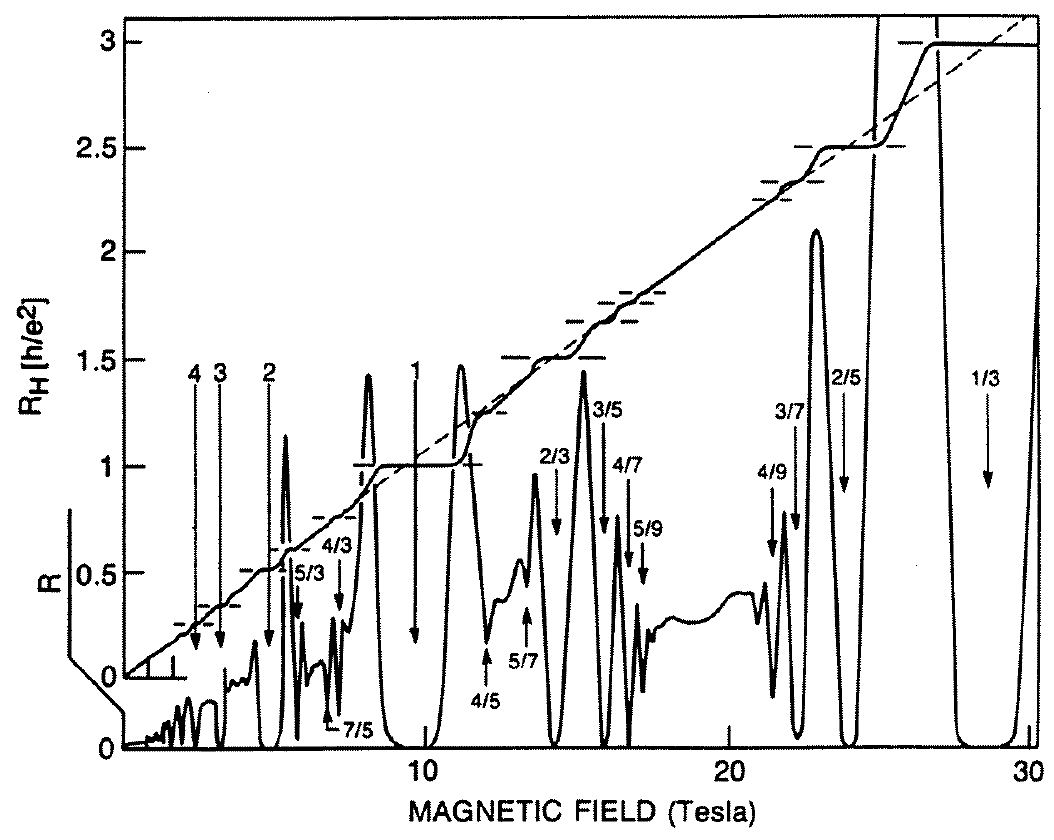
Vorlesung von PD Dr. Marcus Kasner im Wintersemester 2019/20



Die Quanten-Hall-Effekte

Vorlesung: Freitag, 8.30-10.00 Uhr
Beginn: Freitag, den 18. Oktober 2019
Ort: Raum Phys 01.114, Theoretische Physik
15 Veranstaltungen
Übungen sind nicht vorgesehen


Anfang der 80er Jahre wurden bei Experimenten an zweidimensionalen Elektronengasen im starken Magnetfeld überraschende Eigenschaften des elektrischen Transports beobachtet. So fand Klaus von Klitzing bei Temperaturen im Kelvin-Bereich für den Hall-Widerstand eine treppenartige Struktur, deren Plateaus sich um ganzzahlige Füllfaktoren (ein Maß für die Besetzung der Landau-Niveaus, das umgekehrt proportional zur Stärke des Magnetfeldes ist) herum gruppieren. Diese Entdeckung begründete den ganzzahligen Quanten-Hall-Effekt (IQHE).
Nur zwei Jahre später wurde mit noch reineren Proben und in noch stärkeren Magnetfeldern ein ähnliches Verhalten beobachtet, nun allerdings bei bestimmten gebrochenzahligen Füllfaktoren. Dieses Phänomen wird als gebrochenzahliger Quanten-Hall-Effekt (FQHE) bezeichnet.
Schließlich fand man vor einigen Jahren einen neuartigen Quanten-Hall-Effekt in Graphen, einer einlagigen Kohlenstoffmodifikation, dies allerdings bereits bei Zimmertemperatur.
Diese drei Entdeckungen wurden mit den Physik-Nobelpreisen der Jahre 1985, 1998 und 2010 gewürdigt.

Bild: Hall- und longitudinaler Widerstand

Abb.: Das Bild zeigt das typische stufenartige Verhalten des Hall-Widerstandes RH und den verschwindenden longitudinalen Widerstand R im Plateaubereich sowohl für den ganzzahligen als auch den gebrochenzahligen Quanten-Hall-Effekt. Die Plateaus sind durch die jeweiligen Füllfaktoren, s. Pfeile, gekennzeichnet. [R. Willett et al., 1987]

In der Vorlesung behandeln wir die folgenden Themen:
  1. Beschreibung der verschiedenartigen zweidimensionalen Elektronensysteme
  2. Klassische und quantenmechanische Beschreibung eines Teilchens im Magnetfeld
  3. Berechnung von Hall- und Magnetoleitfähigkeit, der Schubnikow-de Haas-Effekt und die Beziehung zur Drude-Theorie
  4. Der ganzzahlige Quanten-Hall-Effekt: die Rolle der Unordnung, die Beziehung zur Anderson-Lokalisierung, die Begründung der Transporteigenschaften, der Einfluss der Wechselwirkung auf die thermodynamischen Eigenschaften, Skyrmionen
  5. Der gebrochenzahlige Quanten-Hall-Effekt: Laughlins Grundzustands-Wellenfunktion, Quasiteilchen, gebrochenzahlige Ladungen, Anyonen und die composite fermion-Theorie von Jain
  6. Der Quanten-Hall-Effekt in Graphen: pseudo-relativistische Bandstruktur und das Transportverhalten

Literatur:
  • T. Chakraborty and P. Pietiläinen, The fractional quantum Hall effect: Properties of an imcompressible liquid, Springer, 1995.
  • S. Das Sarma and A. Pinczuk (eds.), Perspectives in quantum Hall effects: Novel quantum liquids in low-dimensional semiconductor structures, Wiley, 1997.
  • O. Heinonen (ed.), Composite fermions: a unified view of the quantum Hall regime, World Scientific, 1998.
  • A.H.Castro Neto et al., The electronic properties of graphene, Rev. Mod. Phys. 81, 109 (2009).


 
kasner   [ 25-Sep-19 ]