Beispiele für einfache Quantensysteme
- Löse die Schrödinger-Gleichung für den eindimensionalen Potentialtopf.

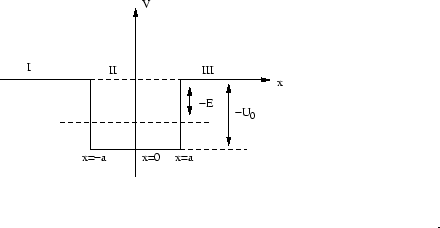
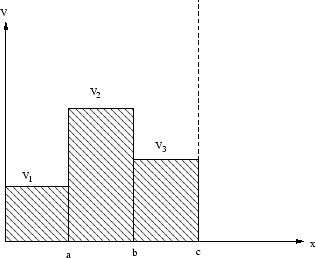
- Manche Potentiale lassen sich durch stückweise konstante Potentiale approximieren. Bestimme die Eigenwertbedingung für das Potential:

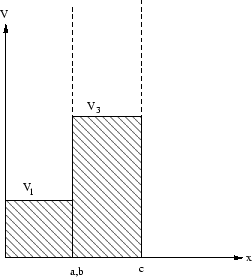
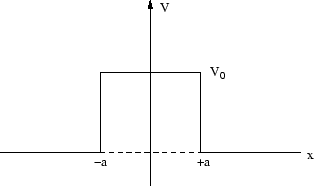
- Betrachte die Schrödinger-Gleichung für folgendes Potential
Die Gebiete
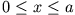 und
und
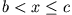 sind zusätzlich bei
sind zusätzlich bei 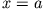 durch eine unendlich dünne und hohe Potentialwand getrennt. Welchen Einfluss hat sie
auf die Lösung der Schrödinger-Gleichung?
durch eine unendlich dünne und hohe Potentialwand getrennt. Welchen Einfluss hat sie
auf die Lösung der Schrödinger-Gleichung?

- Zeige, dass die Wellenfunktion für die Streuung einer (von links nach rechts laufenden) ebenen Welle an der Potentialbarriere
gleich
ist, wobei
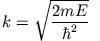 und und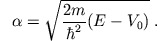 |
|
Betrachte die Fälle 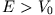 und
und 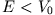 ; wie verhält sich der Transmissionskoeffizient
; wie verhält sich der Transmissionskoeffizient
bei festem 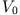 als Funktion der Energie?
als Funktion der Energie?

- Zeige, dass es auch bei der Streuung (
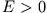 ) am rechteckigen Potentialtopf
) am rechteckigen Potentialtopf
sinnvoll ist, einen Transmissionskoeffizienten zu definieren.
Berechne die Wellenfunktion und diskutiere  in Abhängigkeit von
in Abhängigkeit von 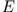 bei festem
bei festem 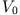 .
.

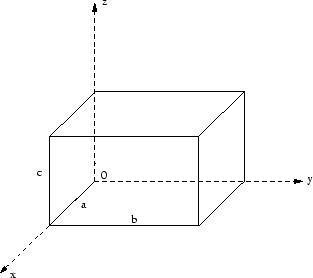
- Ein Teilchen ist eingeschlossen in eine rechteckige Box mit undurchdringlichen Wänden, in der es sich frei bewegen kann.
- a)
- Berechnen Sie die Eigenfunktionen und möglichen Energien.
- b)
- Was können Sie über Entartung der Wellenfunktion aussagen, d.h. existieren mehrere linear unabhängige
Wellenfunktionen zum gleichen Energieeigenwert?

- a)
- Ein Teilchen der Masse
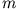 sei in einem eindimensionalen harmonischen Potential. Zur Zeit
sei in einem eindimensionalen harmonischen Potential. Zur Zeit  sei die normierte Wellenfunktion
gegeben durch
sei die normierte Wellenfunktion
gegeben durch
wobei
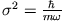 eine Konstante ist. Finden Sie die Wahrscheinlichkeit dafür, dass der Impuls des Teilchens zur
Zeit
eine Konstante ist. Finden Sie die Wahrscheinlichkeit dafür, dass der Impuls des Teilchens zur
Zeit 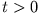 positiv ist.
positiv ist.
- b)
- Betrachten Sie einen eindimensionalen Oszillator im n-ten Energiezustand. Berechnen Sie die Erwartungswerte
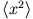 ,
,
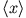 ,
,
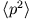 ,
,
 und die Matrixelemente
und die Matrixelemente
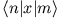 ,
,
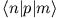 .
Benutzen Sie dazu die Operatoren
.
Benutzen Sie dazu die Operatoren 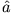 und
und
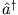 . Was können Sie über die Unschärferelation
. Was können Sie über die Unschärferelation
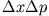 aussagen?
aussagen?
- c)
- Lösen Sie das Problem des harmonischen Oszillators in Impuls-Darstellung.

- Man berechne die Energieniveaus für ein Teilchen in dem Feld mit der potentiellen Energie
für 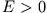 .
.

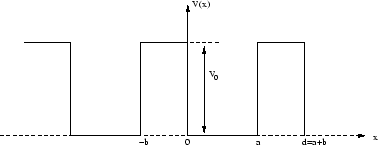
- Zeigen Sie, dass das Energiespektrum eines Teilchens in dem periodischen Potential
eine Bandstruktur hat. Anleitung:
- a)
- Wie ist der Einfluss des periodischen Potentials auf die Wellenfunktion?
- b)
- Durch die Stetigkeitsbedingungen bekommen Sie 4 Gleichungen für die Koeffizienten in den Ansätzen für die Wellenfunktionen.
Nichttriviale Lösungen erhalten Sie, wenn die Determinante der Koeffizienten verschwindet.
- c)
- Unterscheiden Sie die Fälle
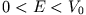 und
und 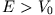 . Um das Spektrum zu untersuchen, lassen Sie
. Um das Spektrum zu untersuchen, lassen Sie 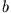 gegen Null und
gegen Null und 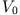 gegen unendlich
gehen derart, dass
gegen unendlich
gehen derart, dass 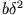 endlich bleibt, wobei
endlich bleibt, wobei
ist.
Für welches physikalische System ist dieses Potential eine Approximation?

- a)
- Der Drehimpulsoperator
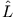 ist definiert als
ist definiert als
Nutzen Sie die Kommutatorrelationen zwischen 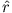 und
und 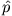 um folgende Kommutationsrelationen zu finden:
um folgende Kommutationsrelationen zu finden:
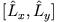 ,
,
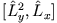 ,
,
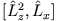 ,
,
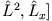 .
.
- b)
- Der Paritätsoperator
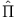 ist definiert durch
ist definiert durch
- i)
- Sei
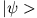 ein beliebiger Ket mit korrespondierender Wellenfuktion
ein beliebiger Ket mit korrespondierender Wellenfuktion
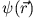 . Finden Sie die Wellenfunktion
. Finden Sie die Wellenfunktion
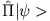 .
.
- ii)
- Zeigen Sie, dass
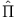 hermitesch ist.
hermitesch ist.
- iii)
- Finden Sie den Operator
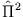 . Was sind seine möglichen Eigenwerte?
. Was sind seine möglichen Eigenwerte?
- iv)
- Wir definieren
Zeigen Sie, dass 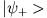 und
und 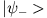 Eigenvektoren zu
Eigenvektoren zu 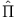 sind.
sind.
- v)
- Zeigen Sie, dass die zu
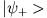 und
und 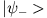 gehörenden Wellenfunktionen gerade bzw. ungerade Funktionen sind.
gehörenden Wellenfunktionen gerade bzw. ungerade Funktionen sind.
- c)
- Besitzt der Projektionsoperator
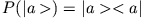 ein Inverses?
ein Inverses?

- In einer Basis
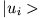 seien die Operatoren
seien die Operatoren 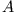 und
und 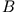 dargestellt durch die Matrizen
dargestellt durch die Matrizen 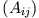 und
und 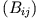 .
Das Ket
.
Das Ket 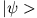 ist durch
ist durch 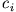 , das Bra
, das Bra 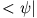 durch
durch 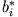 dargestellt.
dargestellt.
- a)
- Finden Sie die Matrixdarstellung des Operators
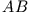 .
.
- b)
- Finden Sie die Darstellung von
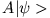 .
.
- c)
- Finden Sie einen Ausdruck für den Skalar
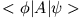 ausgedrückt durch obige Darstellungen.
ausgedrückt durch obige Darstellungen.
- d)
- Was ist die Matrixdarstellung von
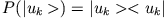 ?
?

- a)
- Berechne das mittlere Potential des Feldes, das vom Kern und dem Elektron im Grundzustand des Wasserstoffatoms erzeugt wird.
- b)
- Diskutiere die Lösung für
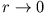 und
und
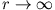 .
.

- a)
- Gegeben sei die Wellenfunktion für ein wasserstoffartiges Atom:
wobei 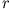 in Einheiten des Bohrschen Radius
in Einheiten des Bohrschen Radius 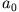 ausgedrückt ist.
ausgedrückt ist.
- i)
- Finden Sie die korrespondierenden Werte der Quantenzahlen
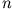 ,
, 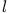 ,
, 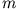 .
.
- ii)
- Konstruieren Sie ausgehend von
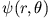 eine andere Wellenfunktion mit den gleichen Werten
eine andere Wellenfunktion mit den gleichen Werten 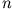 und
und 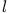 , aber mit einer
anderen magnetischen Quantenzahl,
, aber mit einer
anderen magnetischen Quantenzahl, 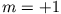 .
.
- iii)
- Berechnen Sie den wahrscheinlichsten Wert von
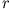 für ein Elektron in dem zu
für ein Elektron in dem zu  korrespondierenden Zustand und mit
korrespondierenden Zustand und mit
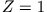 .
.
- b)
- Die Wellenfunktion eines Elektrons in einem wasserstoffartigen Atom sei
mit 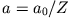 . Die Kernladungszahl ist
. Die Kernladungszahl ist 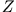 und das Atom enthält nur ein Elektron.
und das Atom enthält nur ein Elektron.
- i)
- Berechnen Sie die Normierungskonstante.
- ii)
- Für den Kern sei
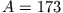 ,
,  . Der Radius des Kerns ist näherungsweise gegeben durch
. Der Radius des Kerns ist näherungsweise gegeben durch
 . Wie groß ist die
Wahrscheinlichkeit, dass sich das Elektron im Kern befindet?
. Wie groß ist die
Wahrscheinlichkeit, dass sich das Elektron im Kern befindet?

- a)
- Zeige, dass für ein kugelsymmetrische Potential
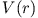 gilt
gilt
- b)
- Welche Konsequenzen hat die Vertauschbarkeit von
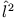 und
und 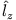 mit dem Hamilton-Operator für die Lösung der
stationären Schrödinger-Gleichung mit kugelsymmetrischem Potential?
mit dem Hamilton-Operator für die Lösung der
stationären Schrödinger-Gleichung mit kugelsymmetrischem Potential?

- a)
- Betrachten Sie die folgenden Beziehungen:
Ein System habe den Drehimpuls  . Finden Sie die Matrixdarstellungen von
. Finden Sie die Matrixdarstellungen von 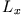 ,
, 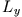 ,
, 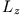 und
und 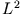 in der Basis der Eigenvektoren von
in der Basis der Eigenvektoren von 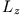 und
und 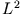 .
.
- b)
- Was ist die Wahrscheinlichkeit dafür, dass eine Messung von
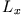
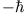 , 0,
, 0, 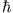 für ein System mit Drehimpuls 1
ergibt. Das System sei im Zustand
für ein System mit Drehimpuls 1
ergibt. Das System sei im Zustand
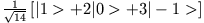 , ausgedrückt in der Basis der Eigenfunktionen von
, ausgedrückt in der Basis der Eigenfunktionen von 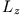 .
.

 Druckversion der Aufgaben
Druckversion der Aufgaben
 Druckversion der Lösungen
Druckversion der Lösungen
M. Keim, H.J. Lüdde
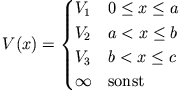
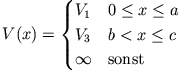
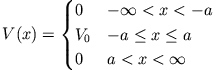
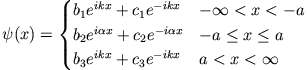
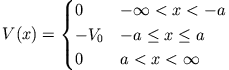

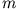 sei in einem eindimensionalen harmonischen Potential. Zur Zeit
sei in einem eindimensionalen harmonischen Potential. Zur Zeit  sei die normierte Wellenfunktion
gegeben durch
sei die normierte Wellenfunktion
gegeben durch
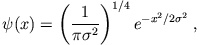
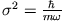 eine Konstante ist. Finden Sie die Wahrscheinlichkeit dafür, dass der Impuls des Teilchens zur
Zeit
eine Konstante ist. Finden Sie die Wahrscheinlichkeit dafür, dass der Impuls des Teilchens zur
Zeit 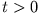 positiv ist.
positiv ist.
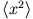 ,
,
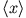 ,
,
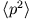 ,
,
 und die Matrixelemente
und die Matrixelemente
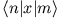 ,
,
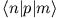 .
Benutzen Sie dazu die Operatoren
.
Benutzen Sie dazu die Operatoren 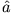 und
und
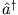 . Was können Sie über die Unschärferelation
. Was können Sie über die Unschärferelation
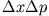 aussagen?
aussagen?
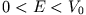 und
und 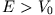 . Um das Spektrum zu untersuchen, lassen Sie
. Um das Spektrum zu untersuchen, lassen Sie 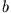 gegen Null und
gegen Null und 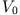 gegen unendlich
gehen derart, dass
gegen unendlich
gehen derart, dass 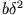 endlich bleibt, wobei
endlich bleibt, wobei
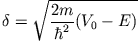
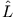 ist definiert als
ist definiert als
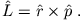
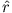 und
und 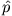 um folgende Kommutationsrelationen zu finden:
um folgende Kommutationsrelationen zu finden:
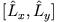 ,
,
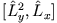 ,
,
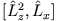 ,
,
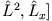 .
.
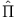 ist definiert durch
ist definiert durch
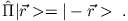
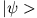 ein beliebiger Ket mit korrespondierender Wellenfuktion
ein beliebiger Ket mit korrespondierender Wellenfuktion
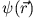 . Finden Sie die Wellenfunktion
. Finden Sie die Wellenfunktion
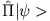 .
.
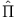 hermitesch ist.
hermitesch ist.
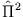 . Was sind seine möglichen Eigenwerte?
. Was sind seine möglichen Eigenwerte?
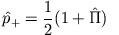

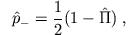
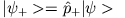

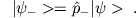
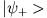 und
und 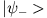 Eigenvektoren zu
Eigenvektoren zu 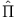 sind.
sind.
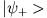 und
und 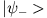 gehörenden Wellenfunktionen gerade bzw. ungerade Funktionen sind.
gehörenden Wellenfunktionen gerade bzw. ungerade Funktionen sind.
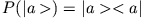 ein Inverses?
ein Inverses?
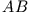 .
.
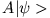 .
.
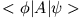 ausgedrückt durch obige Darstellungen.
ausgedrückt durch obige Darstellungen.
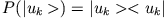 ?
?
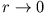 und
und
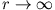 .
.
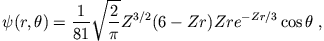
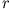 in Einheiten des Bohrschen Radius
in Einheiten des Bohrschen Radius 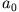 ausgedrückt ist.
ausgedrückt ist.
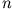 ,
, 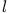 ,
, 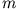 .
.
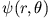 eine andere Wellenfunktion mit den gleichen Werten
eine andere Wellenfunktion mit den gleichen Werten 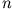 und
und 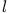 , aber mit einer
anderen magnetischen Quantenzahl,
, aber mit einer
anderen magnetischen Quantenzahl, 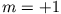 .
.
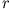 für ein Elektron in dem zu
für ein Elektron in dem zu  korrespondierenden Zustand und mit
korrespondierenden Zustand und mit
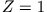 .
.
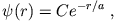
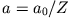 . Die Kernladungszahl ist
. Die Kernladungszahl ist 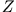 und das Atom enthält nur ein Elektron.
und das Atom enthält nur ein Elektron.
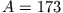 ,
,  . Der Radius des Kerns ist näherungsweise gegeben durch
. Der Radius des Kerns ist näherungsweise gegeben durch
 . Wie groß ist die
Wahrscheinlichkeit, dass sich das Elektron im Kern befindet?
. Wie groß ist die
Wahrscheinlichkeit, dass sich das Elektron im Kern befindet?
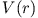 gilt
gilt
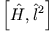

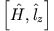

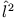 und
und 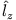 mit dem Hamilton-Operator für die Lösung der
stationären Schrödinger-Gleichung mit kugelsymmetrischem Potential?
mit dem Hamilton-Operator für die Lösung der
stationären Schrödinger-Gleichung mit kugelsymmetrischem Potential?
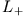

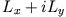
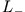

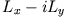
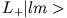

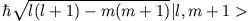
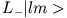

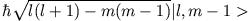
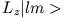

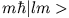
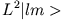

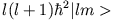
 . Finden Sie die Matrixdarstellungen von
. Finden Sie die Matrixdarstellungen von 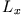 ,
, 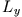 ,
, 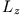 und
und 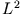 in der Basis der Eigenvektoren von
in der Basis der Eigenvektoren von 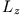 und
und 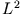 .
.
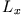
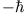 , 0,
, 0, 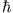 für ein System mit Drehimpuls 1
ergibt. Das System sei im Zustand
für ein System mit Drehimpuls 1
ergibt. Das System sei im Zustand
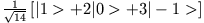 , ausgedrückt in der Basis der Eigenfunktionen von
, ausgedrückt in der Basis der Eigenfunktionen von 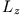 .
.