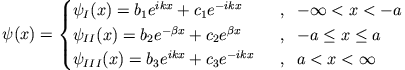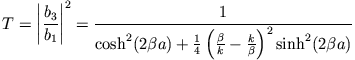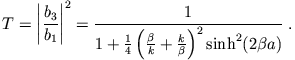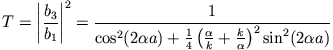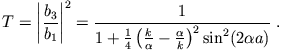Die Schrödinger-Gleichung lautet
- a)
- Sei
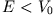, dann ist 
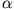rein imaginär, d.h. die Lösung der Schrödinger-Gleichung lautet:
mit
.
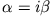Die Konstanten
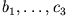lassen sich über die Stetigkeitsbedingungen von 
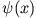bei 
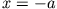und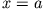 
bestimmen.
Es muss gelten
Man erhält die Gleichungen
und
Aus (1) folgt
 |
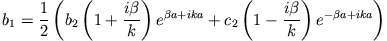(3) |
und aus (2)
Angenommen, die ebene Welle laufe von links nach rechts, dann ist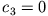 
und Einsetzen von (4) in (3) ergibt
wobei
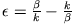ist. Für den Transmissionskoeffizienten findet man
und mit
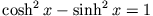
- b)
- Im Fall
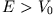ist 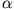reell und man erhält analog zu a)
und
Aus (5) folgt
 |
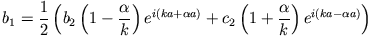(7) |
und aus (6)
Da die Welle aber nur von links nach rechts laufen soll, gilt 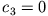. Einsetzen von (8) in (7) ergibt
mit
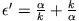ist. Für den Transmissionskoeffizienten findet man
und mit
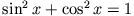
Aus den so hergeleiteten Ausdrücken für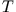 
geht hervor, dass das Teilchen auch bei 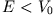eine endliche
Tunnelwahrscheinlichkeit besitzt, was nach den
Vorstellungen der klassischen Physik unmöglich ist.
Wenn 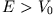ist, erreich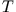t nur für die Werte einiger Resonanzenergien den der
klassischen Mechanik entsprechenden Wert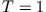 
(
).
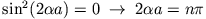M. Keim, H.J. Lüdde
