8

Die Schrödinger-Gleichung lautet:

Wir führen die neue Variable

ein und die Beziehungen

Durch obige Substitution

mit

und einige Umformungen nimmt die Schrödinger-Gleichung dann folgende Form an :

Asymptotische Lösungen:
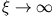verhält sich 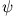wie
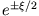
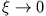ist 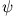proportional zu .
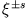Damit die Lösung endlich bleibt, scheiden 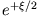und 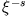als asymptotische Lösungen aus. Wir substituieren

und erhalten für 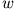die Gleichung

die unter der folgenden Bedingung gelöst werden muss: 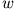ist für 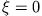endlich und wird für 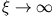nicht schneller als eine endliche Potenz von 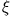unendlich. Die obige Differentialgleichung für 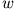ist die Differentialgleichung für die konfluente hypergeometrische Funktion

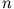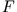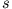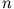Eine Lösung, die die geforderten Bedingungen erfüllt, ergibt sich für nicht-negatives ganzzahliges ( wird zum Polynom). Aus den Definitionsgleichungen für und erhalten wir für die Energieniveaus die Werte:

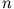durchläuft dabei die positiven ganzzahligen Werte von Null an bis zu dem größten Wert für den noch

ist. Das diskrete Spektrum enthält also eine beschränkte Folge von Niveaus. Für

gibt es überhaupt kein diskretes Spektrum.