- a)
- Wir gehen in den Impulsraum und schreiben
Unsere gesuchte Wahrscheinlichkeit ist
 |
(1) |
Es gilt natürlich:
 beliebig |
(2) |
Für den harmonischen Oszillator gilt:
 |
(3) |
d.h. die Zeitentwicklung ändert nichts an Paritätseigenfunktionen. Es gilt
und
damit
und mit (3)
. Aus (2) erhalten wir dann
also das Ergebnis
.
- b)
- Wir rekapitulieren die Eigenschaften der Erzeuger
und Vernichter 
des harmonischen Oszillators:
mit
und
bzw.
und
Es gelten weiter die Kommutatorbeziehungen
Mit
der Wellenfunktion im n-ten Zustand gilt:
Wir beginnen mit
Mit den obigen Definitionen findet man
und nach weiterer Umformung
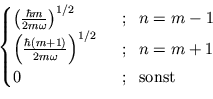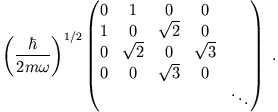Völlig analog folgt
:
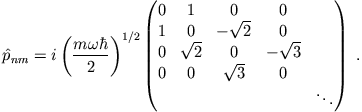Der Oszillator ist im n-ten Zustand:
Mit den obigen Beziehungen folgt dann sofort für die Erwartungswerte 
und 
:
Für die Quadrate
und
berechnen wir erst
und
Damit erhalten wir für
und
:
und
Für die Abweichungen 
und 
findet man
und
Es ist also
. Für den Grundzustand
erhalten wir also
, den nach der Unschärferelation kleinstmöglichen Wert des kanonisch konjugierten
Variablenpaares 
und 
.
- c)
- Wir wechseln in den Impulsraum:
und damit
Zu lösen ist
Separationsansatz:
Damit erhalten wir die Eigenwertgleichung
die auch in der Form
mit
geschrieben werden kann.
Dies ist die gleiche Differentialgleichung, die wir im Ortsraum erhalten haben (nur die Konstanten (bzw. 
) sind leicht anders
definiert). Die Lösungen lauten
zum Energiewert
M. Keim, H.J. Lüdde
