| (1) |
und
Definiere
| (2) |
Subtrahiere (1) und (2):
Dies ist aber die Gleichung (1). Daraus ergibt sich
Somit ist
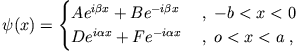 |
mit
Dann muss in der Periode
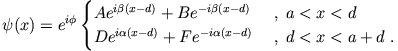 |
Nicht-triviale Lösungen für
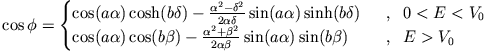 |
mit
Nun unterscheiden wir 2 Fälle:
- I)
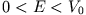 Wir machen nun den in der Aufgabenstellung beschriebenen Grenzübergang
Wir machen nun den in der Aufgabenstellung beschriebenen Grenzübergang
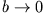 ,
,
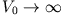 , so dass
, so dass
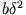 endlich bleibt. Wir definieren
endlich bleibt. Wir definieren
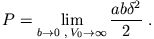
Die Bedingung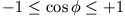 lautet nun:
lautet nun:
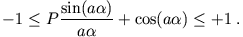
Dies sieht man so: Wir untersuchen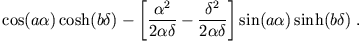
Dies schreiben wir um in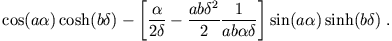
Es ist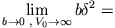 endlich
endlich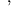
und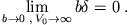
Nun ist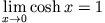
und für kleine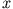 gilt
gilt
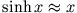 , d.h. der Grenzübergang
, d.h. der Grenzübergang
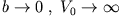 führt auf
führt auf
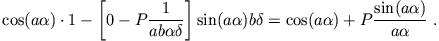
Wir stellen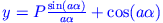 graphisch in Abhängigkeit von
graphisch in Abhängigkeit von 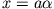 dar und
wählen
dar und
wählen
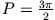 .
Man erkennt, dass das Energiespektrum aus einer Reihe von getrennten Bereichen besteht, innerhalb derer die Energie sich kontinuierlich verändern kann. Diese Bereiche nennt man erlaubte Bänder, die anderen Bereiche verbotene Bänder. Die Breite der erlaubten Bänder steigt mit steigender Energie.
.
Man erkennt, dass das Energiespektrum aus einer Reihe von getrennten Bereichen besteht, innerhalb derer die Energie sich kontinuierlich verändern kann. Diese Bereiche nennt man erlaubte Bänder, die anderen Bereiche verbotene Bänder. Die Breite der erlaubten Bänder steigt mit steigender Energie.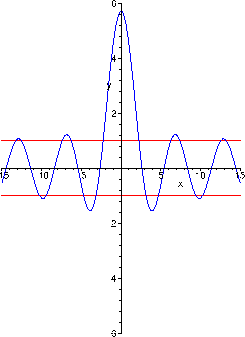
- II)
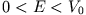 Die möglichen Energiewerte für diesen Fall ergeben sich aus der Bedingung
Die möglichen Energiewerte für diesen Fall ergeben sich aus der Bedingung
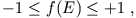
mit
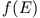

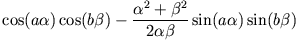

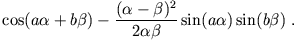
Auch in diesem Fall entsteht wieder eine Bandstruktur.
Anmerkung: Das Modell, das unter der Einführung des oben besprochenen Grenzprozesses enstand, also mit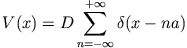
wird als Kronig-Penney-Modell bezeichnet.