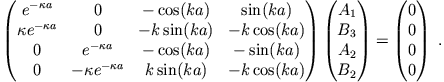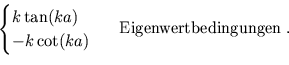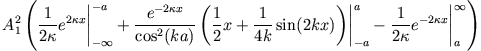Lösung der Schrödinger-Gleichung für die Gebiete I, II und III getrennt. Anpassung der Lösung an den Gebietsgrenzen durch
Stetigkeitsbedingung der Wellenfunktion und Ihrer Ableitung.
Schrödinger-Gleichung und Lösungen für Gebiet I/III:
Schrödinger-Gleichung und Lösung für Gebiet II:
Damit die Gesamtlösung normierbar ist, also die Dichte
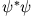 ein Maß für die Aufenthaltswahrscheinlichkeit des Teilchens im
Topf wird, muss
ein Maß für die Aufenthaltswahrscheinlichkeit des Teilchens im
Topf wird, muss 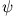 normierbar sein, d.h.
normierbar sein, d.h. 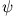 muss für
muss für
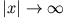 verschwinden.
Man sieht unmittelbar:
verschwinden.
Man sieht unmittelbar: 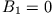 und
und 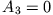 .
Bestimmung von
.
Bestimmung von 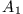 ,
, 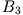 ,
, 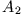 ,
, 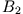 aus Anschlussbedingungen:
aus Anschlussbedingungen:
Dies ist ein lineares homogenes Gleichungssystem mit:
Es besitzt genau dann eine eindeutige nichttriviale Lösung, wenn
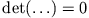 , also:
, also:
Verwende
und
womit folgt
Diese quadratische Gleichung hat die Lösungen
Einsetzen von
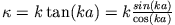 in (2) führt mit (1)
auf die beiden Gleichungen
in (2) führt mit (1)
auf die beiden Gleichungen
Subtrahiert man die erste von der zweiten Gleichung, so findet man
Zusammen mit (3) bleiben also
Man erkennt unmittelbar 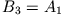 .
.
Einsetzen von
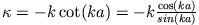 in (2) führt mit (1) und (3) ganz analog auf
in (2) führt mit (1) und (3) ganz analog auf 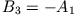 und
und 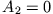 .
.
Gleichung (4) ist in beiden Fällen linear abhängig. Man erhält also zwei Kategorien von Lösungen:
- I)
- symmetrische Eigenfunktionen:
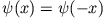
- II)
- antisymmetrische Eigenfunktionen:
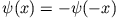
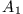 bestimmt sich aus der Normierungsbedingung
bestimmt sich aus der Normierungsbedingung
Für beide Fälle ergibt sich:
Berechnung der Eigenwerte: Einsetzen der Definitionen für 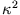 und
und 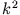 liefert
liefert
da 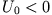 , so dass man für die Eigenwertbedingungen
, so dass man für die Eigenwertbedingungen
oder
erhält.
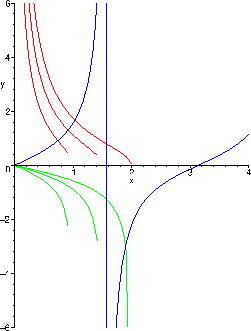
Jeder Schnittpunkt der Kurven
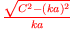 und
und
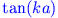 definiert die Eigenwerte zu einer symmetrischen Eigenfunktion,
die Schnittpunkte der Kurven
definiert die Eigenwerte zu einer symmetrischen Eigenfunktion,
die Schnittpunkte der Kurven
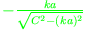 und
und
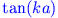 definieren die Eigenwerte zu einer antisymmetrischen Lösung
der Schrödinger-Gleichung.
definieren die Eigenwerte zu einer antisymmetrischen Lösung
der Schrödinger-Gleichung.
M. Keim, H.J. Lüdde