10

a)

Nach Definition gilt

Dabei haben wir benutzt, dass

Nun benutzen wir noch die Beziehung

Also

Weiterhin ergibt sich:

und ähnlich

Schließlich erhalten wir

ebenso

b)

i)

Das ket 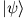schreiben wir als

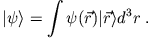
Daraus folgt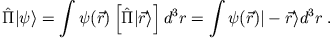

Wir wechseln nun die Integrationsvariable von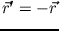 , und erhalten die zu 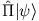korrespondierende Wellenfunktion:

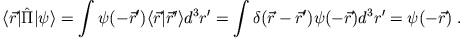
ii)

Aus Teil i) folgt

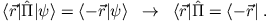
Andererseits ist das hermitesch konjugierte von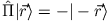

gleich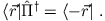

Da dies für alle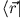 gilt, ist .

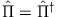iii)

Es ist

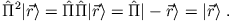
Dies gilt für alle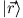 , d.h. .
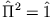Sei nun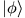 ein Eigenvektor von 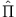mit dem Eigenwert 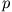, d.h. 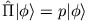. Es ist nun auch

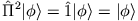
und weiterhin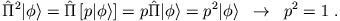

Da aber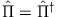 folgt, dass die Eigenwerte von 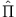reell sein müssen: .

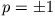iv)

Es ist

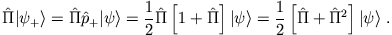
Mit Hilfe von Teil iii) erhalten wir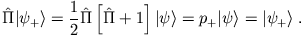

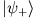ist also ein Eigenvektor von 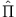mit dem Eigenwert 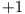. Ähnlich sieht man: 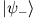ist Eigenvektor zu 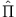mit dem Eigenwert .

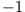v)

Wir wissen bereits:

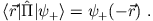
Es ist aber auch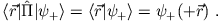

Daraus folgt unmittelbar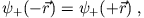

d.h.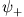 ist eine gerade Funktion. Ähnlich sieht man: 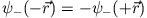, d.h. 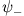ist eine ungerade Funktion.

Bemerkung: Jedes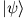 lässt sich schreiben als

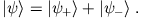
Wir haben hier also eine Methode, um eine Wellenfunktion in gerade und ungerade Anteile zu zerlegen.

c)

Nein, denn er ist keine umkehrbare eindeutige Abbildungsvorschrift. Alle mit denselben werden durch auf denselben Vektor abgebildet: