- a)
- In Kugelkoordinaten lautet der Laplace-Operator
Der Winkelanteil
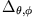 lautet explizit
lautet explizit
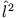 in Kugelkoordinaten:
in Kugelkoordinaten:
Der Laplace-Operator lässt sich also auch wie folgt schreiben:
Dementsprechend lautet der Hamilton-Operator für ein Zentralpotential
Den Kommutator
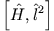 kann man somit aufspalten:
Alle drei Kommutatoren verschwinden - Begründung siehe unten. Analog für
kann man somit aufspalten:
Alle drei Kommutatoren verschwinden - Begründung siehe unten. Analog für
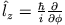 .
.
Wie aus den angegebenen Formeln ersichtlich ist, wirken die Drehimpulsoperatoren nur auf die Winkelkoordinaten, damit ist klar,
dass der erste und dritte Kommutator verschwinden.
Der Kommutator eines Operators mit sich selbst verschwindet ebenfalls, und das Quadrat des Drehimpulsoperators
und der z-Komponente des Drehimpulsoperators kommutieren ebenfalls.
- b)
- Operatoren, die miteinander vertauschen, besitzen einen gemeinsamen Satz Eigenvektoren. Folglich können wir die Eigenfunktionen der
Schrödinger-Gleichung mit kugelsymmetrischem Potential schreiben als
Die Kugelflächenfunktionen
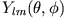 sind Eigenfunktionen zu
sind Eigenfunktionen zu 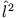 und
und 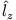 .
.
M. Keim, H.J. Lüdde