Um die Matrixdarstellung von
Wir wählen die Standard-Basis:
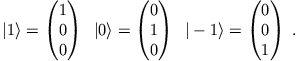 |
Die Matrixdarstellung von
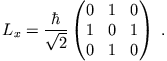 |
Für
Die Matrixdarstellung von
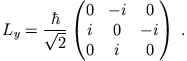 |
Für
| 0 | |||
Die Matrixdarstellung von
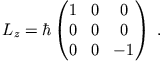 |
Für
Die Matrixdarstellung von
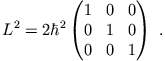 |
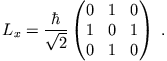 |
Wenn wir die Eigenwerte von
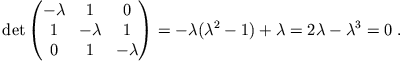 |
Die Lösungen sind
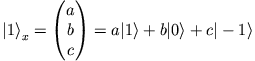 |
mit
Folgendes Gleichungssystem ist also zu lösen:
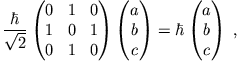 |
d.h.
Daraus erhalten wir
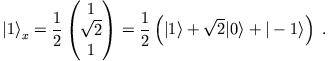 |
Auf gleiche Weise erhalten wir für die zwei anderen Eigenvektoren:
und
Wir schreiben den Systemzustand als
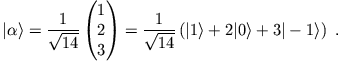 |
In der Basis der Eigenvektoren von
Berechnung der Terme
Ergebnis:
Daraus lassen sich nun die gesuchten Wahrscheinlichkeiten berechnen:
| 0 | |||