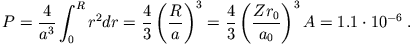- a)
- i)
- Wir betrachten den Exponentialfaktor in
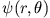 : er hat die Form
: er hat die Form
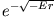 . Da
. Da
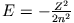 ist,
schließen wir auf
ist,
schließen wir auf 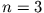 . Die Drehimpulsquantenzahl
. Die Drehimpulsquantenzahl 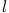 erhalten wir durch Anwendung von
erhalten wir durch Anwendung von 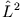 auf
auf 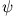 :
:
Wir benutzen 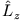 , um die magnetische Quantenzahl
, um die magnetische Quantenzahl 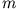 zu finden:
zu finden:
- ii)
- Wir benutzen den Leiteroperator
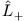 . Es ist
. Es ist 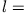 und
und 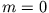 , also
, also
Wir erhalten so
- iii)
- Der wahrscheinlichste Wert von
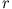 tritt auf, wenn
tritt auf, wenn 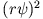 maximal wird. Für
maximal wird. Für 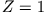 erhalten wir
erhalten wir
Es ergibt sich die quadratische Gleichung
Die Lösungen sind 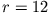 und
und 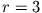 .
. 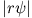 wird maximal für
wird maximal für 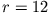 . Der wahrscheinlichste Wert ist also
. Der wahrscheinlichste Wert ist also 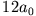 .
.
- b)
- i)
- Zur Normierung muss das Integral
berechnet werden. Da
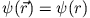 bleibt vom Normierungsintegral
bleibt vom Normierungsintegral
übrig und mit
ist
auszuwerten. Mit der Substitution
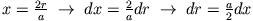 bleibt
bleibt
Dieses Integral kann mit Hilfe der Gamma-Funktion
gelöst werden (hier 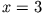 bzw.
bzw. 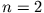 ):
):
- ii)
- Sei
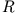 der Kernradius
der Kernradius
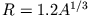 in Fermi (
in Fermi (
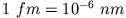 ). Die Wahrscheinlichkeit, das Elektron im Kern zu finden, ist
). Die Wahrscheinlichkeit, das Elektron im Kern zu finden, ist
Da 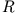 sehr klein ist im Vergleich zu
sehr klein ist im Vergleich zu 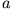 (
(
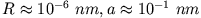 ), betrachten wir
), betrachten wir 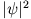 als konstant im Kern, d.h.
als konstant im Kern, d.h.
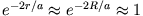 .
Dann folgt unmittelbar
.
Dann folgt unmittelbar
M. Keim, H.J. Lüdde
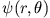 : er hat die Form
: er hat die Form
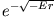 . Da
. Da
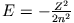 ist,
schließen wir auf
ist,
schließen wir auf 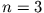 . Die Drehimpulsquantenzahl
. Die Drehimpulsquantenzahl 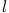 erhalten wir durch Anwendung von
erhalten wir durch Anwendung von 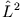 auf
auf 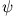 :
:
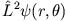

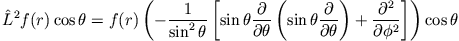



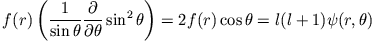
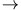
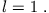
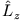 , um die magnetische Quantenzahl
, um die magnetische Quantenzahl 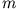 zu finden:
zu finden:
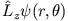

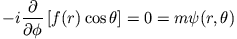
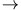
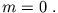
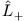 . Es ist
. Es ist 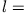 und
und 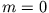 , also
, also
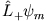

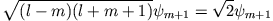
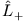

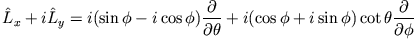
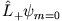

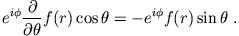
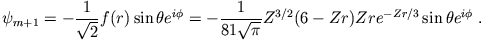
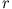 tritt auf, wenn
tritt auf, wenn 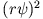 maximal wird. Für
maximal wird. Für 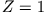 erhalten wir
erhalten wir
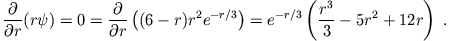
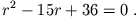
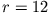 und
und 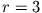 .
. 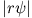 wird maximal für
wird maximal für 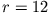 . Der wahrscheinlichste Wert ist also
. Der wahrscheinlichste Wert ist also 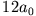 .
.
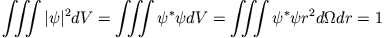
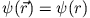 bleibt vom Normierungsintegral
bleibt vom Normierungsintegral
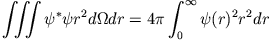
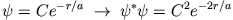
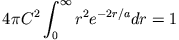
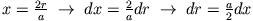 bleibt
bleibt
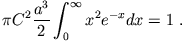

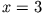 bzw.
bzw. 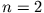 ):
):
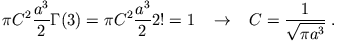
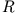 der Kernradius
der Kernradius
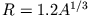 in Fermi (
in Fermi (
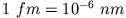 ). Die Wahrscheinlichkeit, das Elektron im Kern zu finden, ist
). Die Wahrscheinlichkeit, das Elektron im Kern zu finden, ist
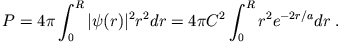
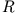 sehr klein ist im Vergleich zu
sehr klein ist im Vergleich zu 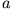 (
(
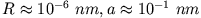 ), betrachten wir
), betrachten wir 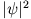 als konstant im Kern, d.h.
als konstant im Kern, d.h.
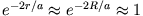 .
Dann folgt unmittelbar
.
Dann folgt unmittelbar