Chapter I 第一章: General Relativity of Compact Stars and Black Holes 致密星和黑洞的广义相对论
One hundred years after Albert Einstein developed the field equations of general relativity and predicted the existence of gravitational waves, his theory triumphantly corroborates all experimental and observational tests it has been put through to date. Among the $\approx$ 2500 known neutron stars (NSs), there are some which are in binary systems where the companion of the NS is either a normal star, a planet, a white dwarf or again a NS. The most impressive binary neutron star system, so far, is the so called 'Double Pulsar: PSR J0737-3039A/B', which has been discovered in 2003. The two neutron stars in this binary system, which are only separated by 800000 km, orbit around each other with an orbital period of 147 minutes and a mean velocity of one million km/h. This system is excellent for testing Einstein's theory of general relativity and alternative theories of gravity in the strong-field regime. Due to the emission of gravitational waves, the distance between the two NSs decreases with time and finally the two objects will merge accompanied by neutrino radiation, a strong gravitational radiation chirp, and short gamma-ray burst.
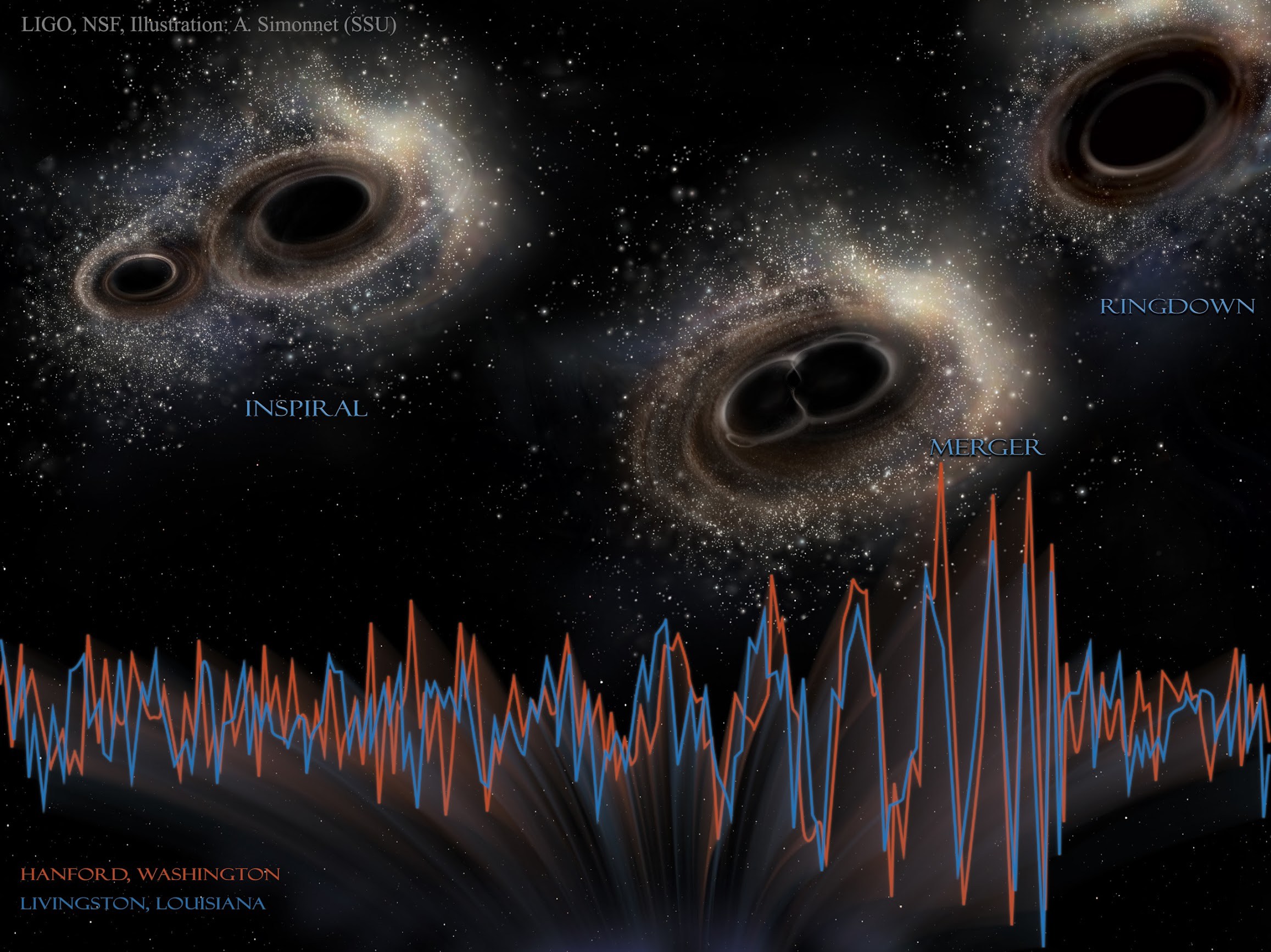
LIGO Detects Gravitational Waves from Merging Black Holes (Astronomy Picture of the Day, 11.02.2016)
Gravitational waves have been recently observed from a pair of merging black holes (BHs) by the LIGO detectors and GWs emitted from merging neutron star binaries are on the verge of their first detection. The main difference between GWs originating from a merger of two BHs or NSs is the possibility of an existence of a post-merger phase after the collisions of the two objects, which can be only present in the case of a NS-merger. Depending on a variety of parameters, e.g. the initial mass of the two stars, the product right after the merger could be a prompt collapse to a BH, a metastable HMNS or a stable supramassive NS. The GWs produced by a merger of NSs are by far more interesting as the GWs resulting from a BH-merger, as, in the case of existence of a post-merger phase, the equation of state (EOS) of elementary matter might be deduced by a frequency analysis of the GW. This is insofar interesting, as the EOS until now is mainly understood by high energy heavy ion collisions and only coarse constraints are coming from astrophysical observations, like the current observational constraint on the observed maximum mass in neutron stars, i.e.,~ $2.01\pm0.04M_\odot$. The first chapter of this lecture will give a short overview about the mathematical groundings of general relativity and the theory and experimental evidences of black holes and compact stars (neutron stars, hybrid stars and strange quark stars). The analytic and numerical solutions of the underlying tensorial equations of general relativity will be solved (in this chapter) by using the computer-algebraic software Maple and by a parallized MPI/OpenMP-C++ program which solves the Tolman-Oppenheimer-Volkov-equation numerically.
General Relativity of Black Holes and Compact Stars 致密星和黑洞的广义相对论
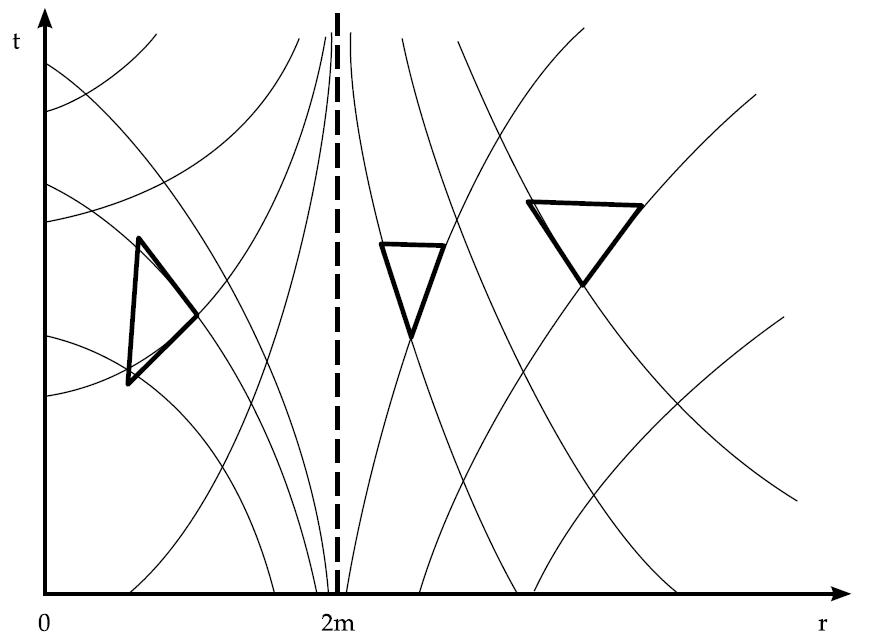
Spacetime diagram of the Schwarzschild metrik in Schwarzschild coordinates.
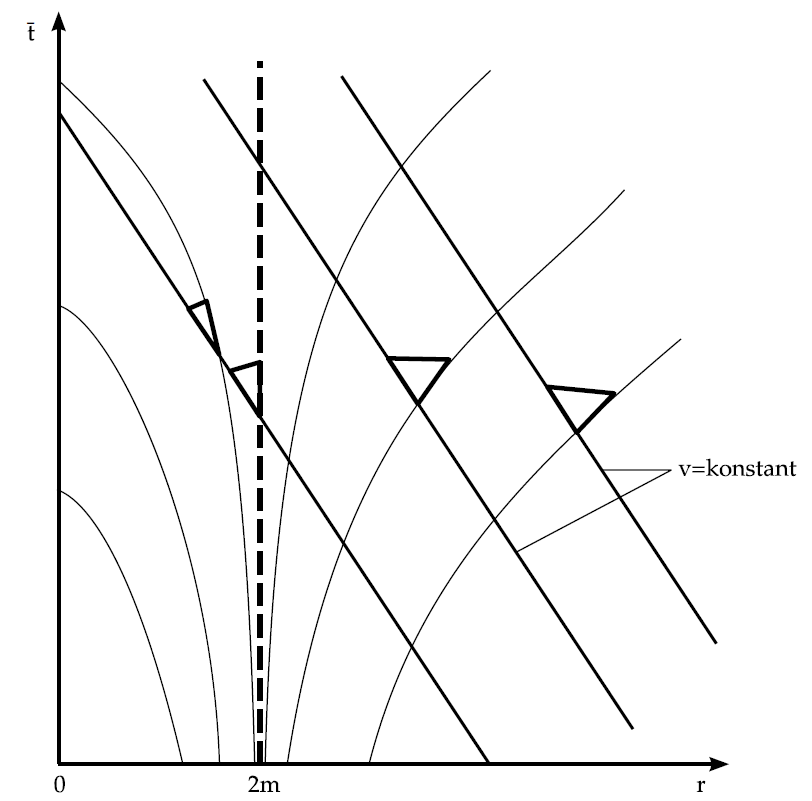
Spacetime diagram of the Schwarzschild metrik in ingoing Eddington–Finkelstein coordinates.
Einstein's theory of general relativity and the resulting general relativistic conservation laws for energy-momentum in
connection with the rest mass conservation are the theoretical groundings of compact stars and gravitational wave emission from colliding compact star binaries:
\[
\begin{eqnarray}
&R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R ~=~ 8 \pi \, T_{\mu\nu}~\nonumber\\
&\nabla_\mu T^{\mu\nu} ~=~ 0~, ~~\nabla_\mu \left( \rho \, u^\mu \right) ~=~ 0 \label{eq:Einstein}&
\end{eqnarray}
\]
$T_{\mu\nu}$ describes the energy-momentum tensor, $R_{\mu\nu}$ is the Ricci tensor, which contains first and second derivatives of the space-time metric $g_{\mu\nu}$, $\nabla_\mu$ is the covariant derivative and $u^\mu$ is the four velocity of the star's fluid. The Einstein equation describes in which way the space-time structure need to bend (left hand side of the equation) if energy-momentum is present (right hand side of the equation). These highly non-linear differential equations describe on the one hand
how matter moves in a curved space-time and on the other hand formulates
in which way the amounts of energy-momentum curves the space-time
structure. Unless explicitly stated, we use in the following units in which $c=G=M_\odot=1$.
Black holes are the most extreme objects in our universe. With the exception of the singular point at the center of a non-rotating chargeless black hole, no matter or energy is present in the system ($T_{\mu\nu} \equiv 0$) and therefore the Einstein equation reduces to $R_{\mu\nu} \equiv 0$. The metric of such a black hole is given by the Schwarzschild metric:
\[
\begin{equation}
g_{\mu\nu} ~~=~~ \hbox{diag}\left( -\left( 1- \frac{2 M}{r} \right) ~,~ \left( 1- \frac{2 M}{r} \right)^{-1} ~,~ r^2 ~,~ r^2 \sin^2 \theta\right)\quad , \label{eq:Schwarzschild}
\end{equation}
\]
where $M$ defines the total mass of the black hole. A real singularity occurs at the center of the black hole ($r=0$), where all of the mass is located and the energy density becomes infinite. The Schwarzschild metric describes the properties of a black hole in a gauge which can be regarded as the viewpoint of an observer at rest which is located at spatial infinity. Apart from the real singularity at $r=0$, a coordinate singularity at $r=2M$ exists where space and time changes their properties. The left diagram in figure illustrates this strange property of the Schwarzschild black hole by visualizing the light cones of in- and outgoing photons in a space-time diagram in Schwarzschild coordinates.
A particle which is falling in such a Schwarzschild black hole will never reach the inner area ($r < 2M$) of the black hole and for the outside observer the object seems to become frozen at the event horizon at $r=2M$. However, the coordinate singularity of the Schwarzschild metric is not a real singularity and a particle falling into a black hole will indeed travel trough the event horizon and reach the center of the black hole in a finite time. This fact can be easily understood if one transforms the coordinate system into a coordinate frame moving with the particle, e.g. the Eddington-Finkelstein coordinates describe a photon falling with the speed of light radially into a black hole from the photon's viewpoint (see right diagram). The space-time diagram clearly shows, that the particle travels trough the event horizon, but has no way to communicate with the outer world if it is inside the black hole at $r<2M$.
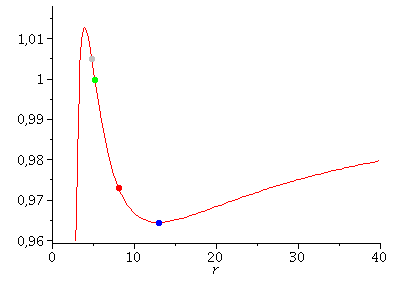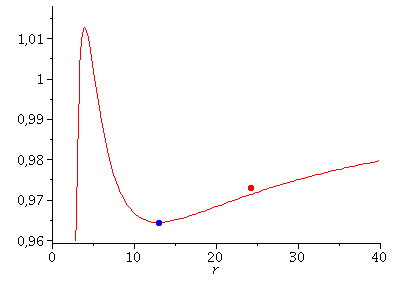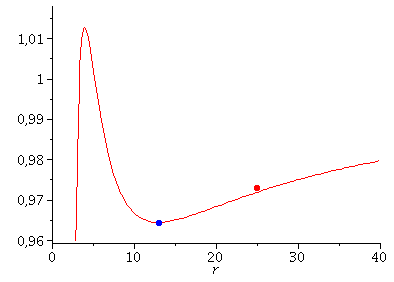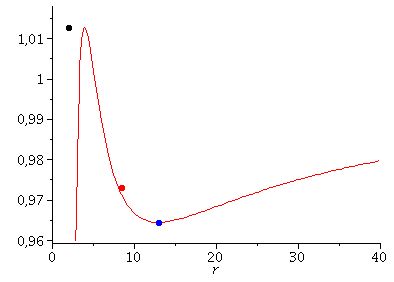
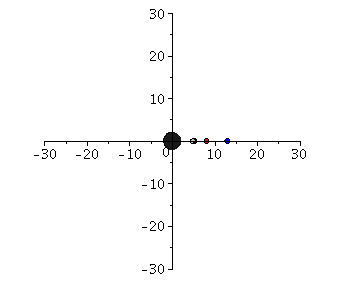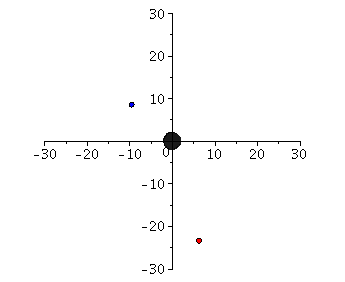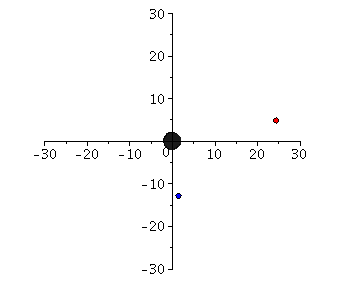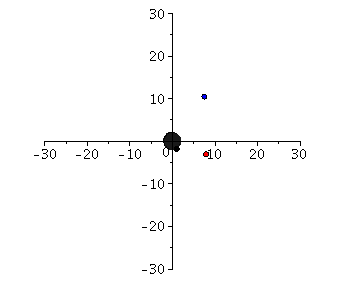Possible paths of test bodies around a non-rotating black hole are classified by means of an effective potential.
Additional Material 附加材料: Introduction in Maple , GR with Maple , GR with Mathematica , Geodesics I , Geodesics II , The Transit of the Mercury in GR
The movement of a test body (mass small compared to the mass of the black hole) around a black hole is an astrophysically very relevant problem. It is almost confirmed that there is a supermassive black hole in the center of our galaxy, and the movement of individual S-stars around this center has been traced for centuries (see e.g. R.Genzel et al.). In addition to these current findings, the perihelion shift of Mercury is considered to be an effect caused by the general theory of relativity. Although the movement of the planets of our solar system around our central star (the sun) certainly does not represent a movement around a black hole, the equations of the planetary motions can be described in good in this approximation (see Birkov's Theorem). In the following maple worksheets the geodetic equation is solved numerically in a given Schwarzschild space-time and the possible paths of test bodies are classified by means of a defined effective potential. In addition to the bound circular (blue) and elliptical (red) orbits, the parabolic (green) and hyperbolic (gray) orbits, a trajectory of a captured orbit (black) is also possible. Additionally the properties of the last stable circular orbit and the photon-sphere is analysed in the maple worksheets.
Compact stars (white dwarfs, neutron stars, strange quark stars and black holes) are the potential final states of the evolution of a normal star. Neutron stars are extremely dense astrophysical objects, which are formed in the center of a supernova explosion. Quark stars are even more compact and they might represent the last stable state before the matter collapses to a black hole. Due to their large magnetic fields (up to $10^{11}$ Tesla) and fast rotation (up to 640 rotations in one second) neutron stars emit a certain electromagnetic spectrum. In our galaxy we currently know about 2500 of these exotic objects, which are mainly observed as pulsars by radio telescopes. Among the known neutron stars, there are some which are in binary systems where the companion of the neutron star is either a normal star, a planet, a white dwarf or again a neutron star; unfortunately a neutron star - black hole binary system has not been found until now.
In contrast to black holes, the energy-momentum tensor $T_{\mu\nu}$ which enters in the Einstein equation is not identical zero. In the ideal-fluid energy-momentum tensor $T_{\mu\nu}=(e+p)~u_\mu u_\nu +
p~g_{\mu\nu}$ enters the energy ($e$) and pressure ($p$) densities of the nuclear and
elementary particle physics contributions of the underlying neutron star
matter and $u^\mu=dx^\mu/d\tau$ describes the four velocity of the star's
fluid which is defined as the derivative of the coordinates
$x^\mu=(t,x,y,z)$ by the proper time $\tau$.
The interior metric of a single, spherically symmetric and static neutron star can be calculated by assuming the following Ansatz of the metric $g_{\mu\nu}$ (infinitesimal line element $ds$)
\[
\begin{equation}
ds^2 ~=~ g_{\mu\nu} \,dx^{\mu}dx^{\nu} ~=~
- e^{2\nu(r)} dt^2
+ \left( 1- \frac{2 m(r)}{r} \right)^{-1} dr^2
+ r^2 d\theta^2
+ r^2 \sin^2 \theta ~d\phi^2 \quad. \label{eq:lineel}
\end{equation}
\]
By inserting this Ansatz of the metric and the expression for the energy momentum tensor into the Einstein equation one derives the Tollman-Openheimer-Volkov (TOV) equations)
\[
\begin{equation}
\frac{dm}{dr} ~=~ 4\pi r^2~e ~, \quad
\frac{d\nu}{dr} ~=~ \frac{m+4 \pi r^3 p}{r \left(2m -r \right)} ~, \quad
\frac{dp}{dr} ~=~ -(e+p) \frac{d\nu}{dr} \quad . \label{eq:TOV}
\end{equation}
\]
For a given equation of state (EOS: a function $p(e)$) the TOV equation can be solved numerically by fixing the central pressure $p_c$ and integrating outwards to the star's surface where the pressure is zero.
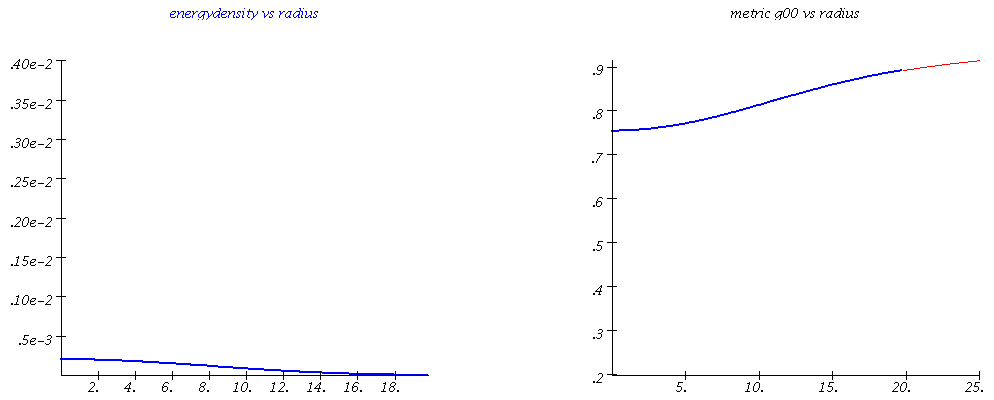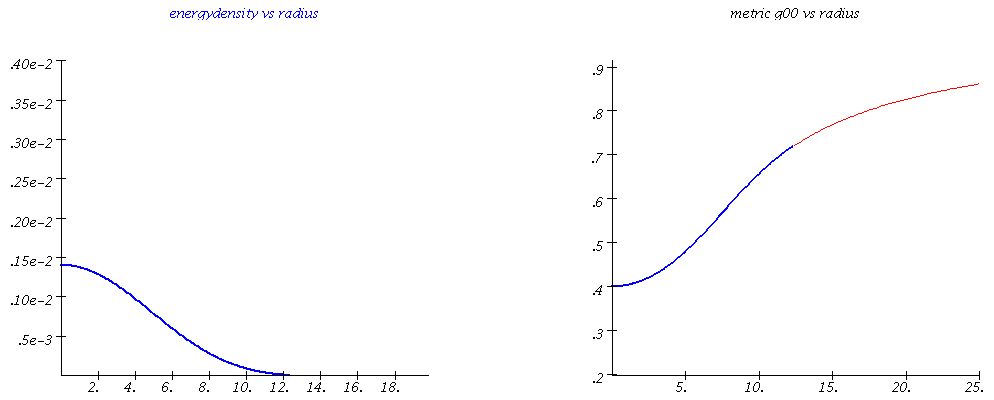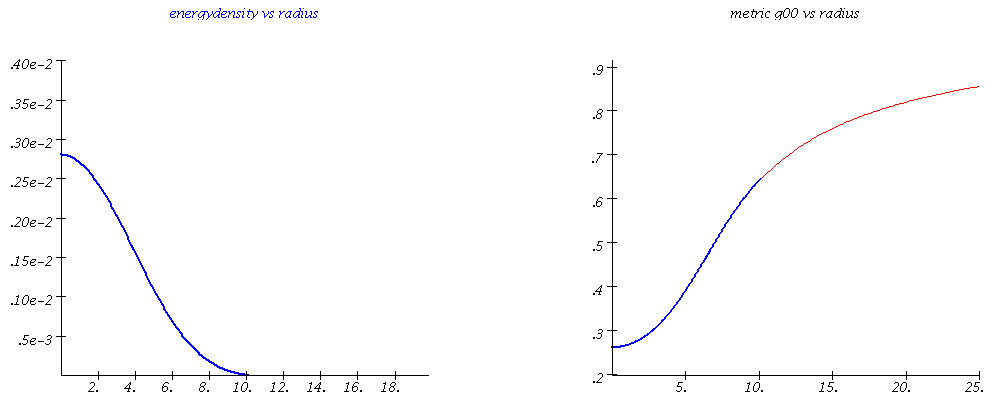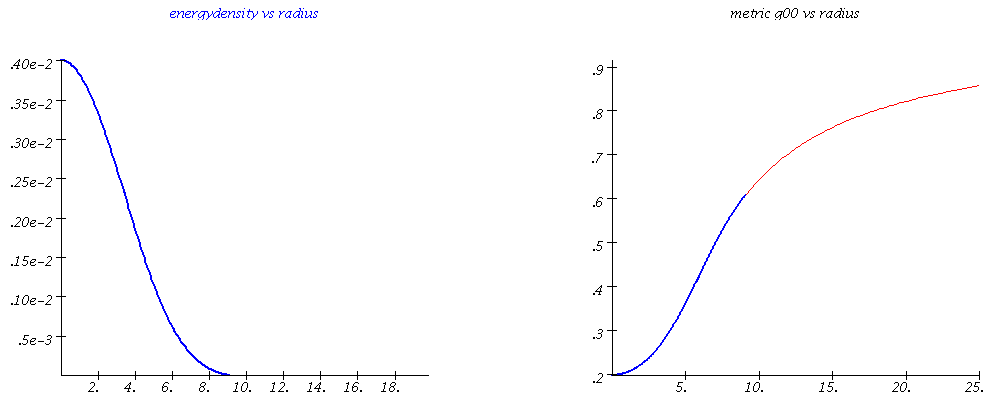Energydensity and spacetime metric-component $g_{00}$ vs radius for different values of the central density (different mass values of the compact star).
Additional Material 附加材料: TOV equation and neutron stars in Maple , C-program (sequential version) , C-program (OpenMP parallel version) , C-program (MPI parallel version) , parallel programming with MPI and OpenMP (in German) , Intro: Parallel Programming
The TOV equation can be deduced and then be solved numerically using Maple. In the left figure, an animation is presented that summarizes these numerical results. The total mass and the radius of the neutron star changes with variation of the central density value of the star. The space-time metric inside and outside the star (for example, the g00 component of the metric, see right figure (blue and red curve)) changes as a function of the radial distance r to the star center. If the spacetime distortion in the interior of the star becomes too great and the total mass of the star exceeds a certain value Mmax, the star becomes unstable and collapses to a black hole. The value of the maximum mass of a neutron star is determined by the state equation of elementary matter. Since in the inner region of the star the density can reach multiple values of the normal nuclear density, it is very likely that a phase transition to quark matter occurs - these stars are referred to as so-called hybrid or quark stars. The TOV equations can also be easily solved using a C/C++ program. The basic concepts of parallel programming can be introduced here using a MPI and OpenMP version of the C/C++ program.
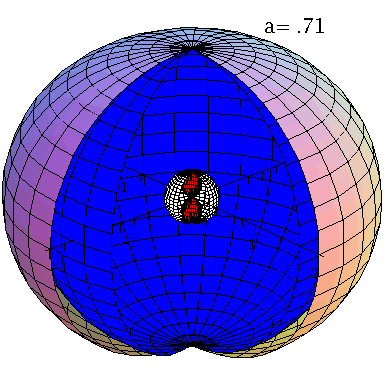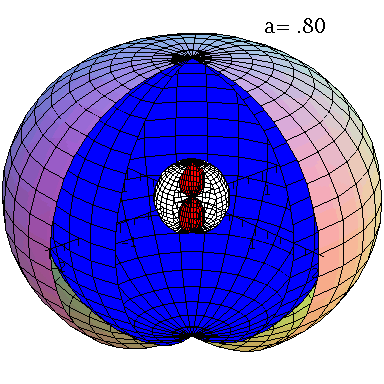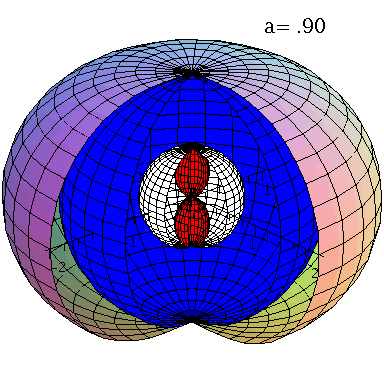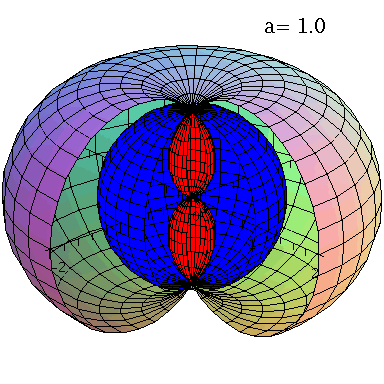
Kerr metric: Horizons and surfaces infinite redshift and stationary borders.
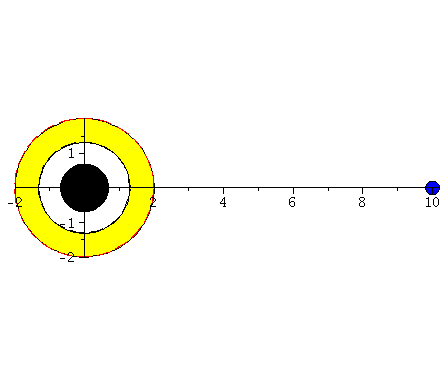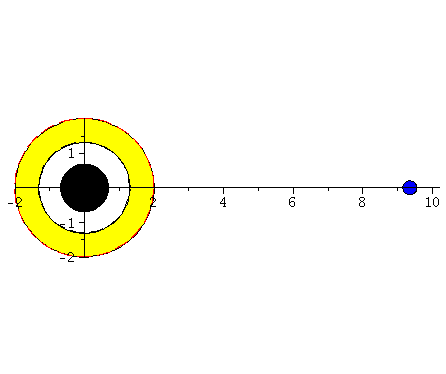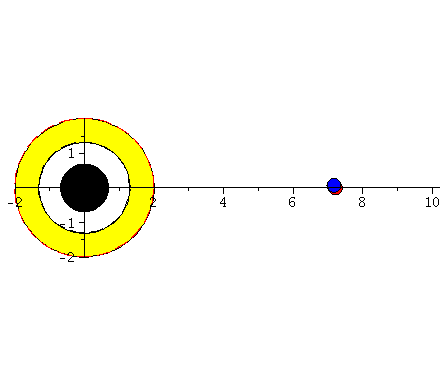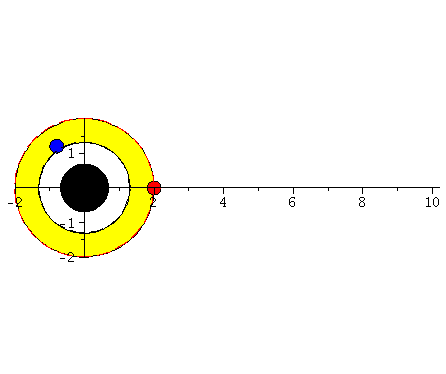
Test mass falling into a rotating (blue) and non-rotating (red) black hole.
It can be shown (Birkov Theorem) that the metrical structure outside the neutron star is identical to the Schwarzschild metric of a black hole. It is impressive that Karl Schwarzschild found this analytical solution of the Einstein equation only three month after Einstein's article and it is very unfortunate that he died soon after his remarkable result. The Schwarzschild solution is only valid in a spherically symmetric approximation and even for a single rotating neutron star the metric outside the body cannot be described analytically, as a similar theorem like the Birkov Theorem does not hold for the Kerr solution of a rotating black hole. However, all of the known NSs, including the individual stars of the famous double PSR J0737-3039A/B, can be described in good approximation with the TOV equations and only in the case of a very cramped binary system tidal deformations become important.
We will see in chapter II and III, that the structure of the space-time metric of the highly differentially rotating hypermassive compact star produced by a system of colliding compact star binaries is very complicated. In addition to the attractive gravitational force a frame dragging related force effects the interior and exterior solution of spacetime. To illustrate this effect, we will look in the following at the properties of the Kerr solution of a rotating black hole and examine the geodetic movement of test masses around this object. Rotating black holes have a more complicated event horizon structure and the surfaces infinite redshift and the interfaces of stationary borders are generally not identical with the horizons. In the case of non-vanishing rotation, there are two horizons (see figure on the left, r+: blue surface and r-: white surface), and there are also two surfaces of infinite redshift (rs+: outer surface and rs-: red surface). The region between the outer surface of infinite redshift and the outer event horizon at r+ is called ergosphere. Here test particles can no longer rotate in counter direction to the rotation of the black hole - so stationary movements are no longer possible.
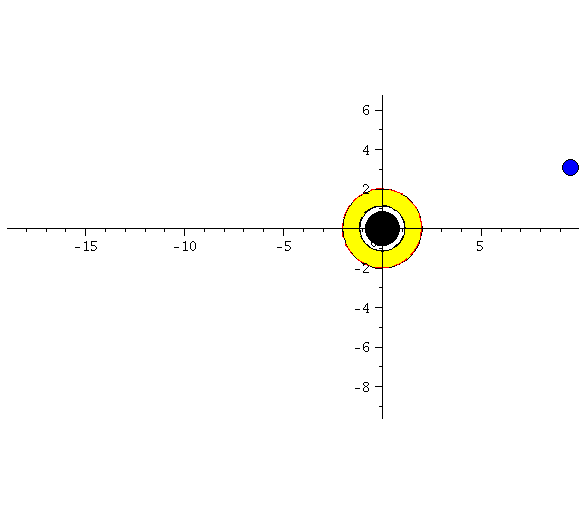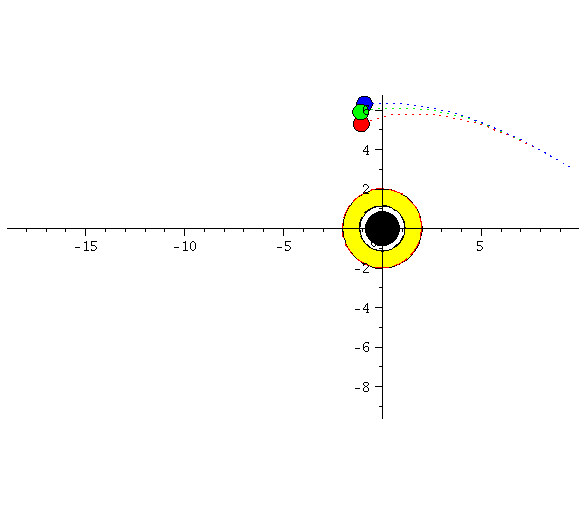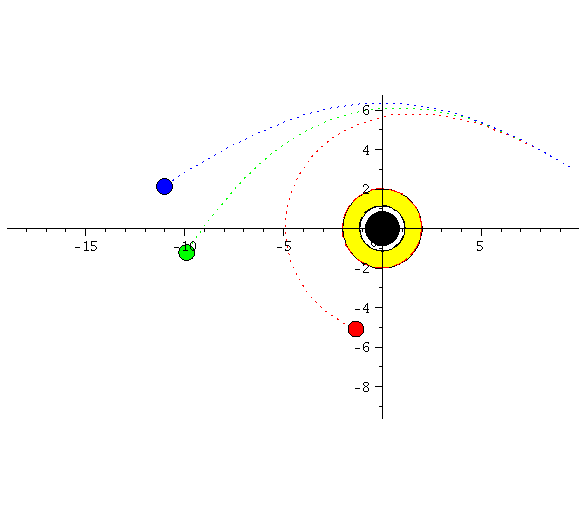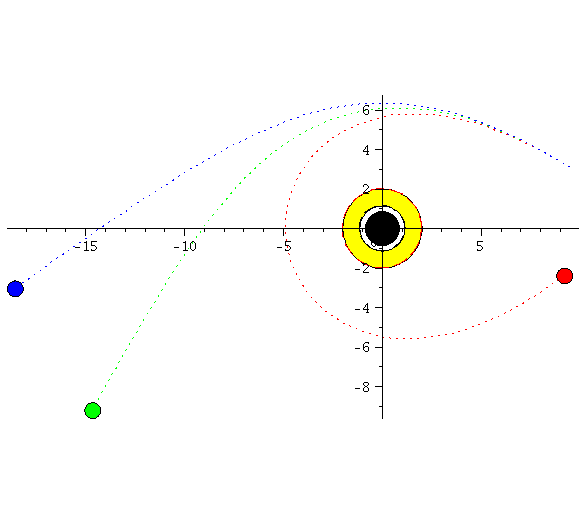Left: the two ISCO's of a Kerr black hole. Right: trajectories around a non-rotating (green), counter-rotating (red) and co-rotating (blue) black hole.
Additional Material 附加材料:
In this appendix you will find several online materials including the Maple worksheets of the horizon structure of the Kerr metric and the geodesic motion around a Kerr black hole. On the internet page of the German lecture Allgemeine Relativiätstheorie mit dem Computer (General Theory of Relativity on the Computer) you will find further-going materials.
Elementary particle physics and the zoo of compact stars 初级粒子物理学和致密星的世界
The zoo of compact stars.
Depending on the model used, the compact star zoo consists of different inhabitants: e.g. neutron stars with and without hyperons, quark stars and strange quark stars, hybrid stars with color superconducting quark matter, hybrid stars with Bose-Einstein condensates of antikaons. At which density the phase transition to the Quark-Gluon-Plasma appears and a detailed analysis of the properties of this transition is still somewhat uncertain. The theoretical modelling is often still based on effective theories of the QCD interaction and therefore different species of compact stars are possible. A hybrid model of a compact star is realized by a construction of a phase
transition between a hadronic model and a quark model. In contrast to the Maxwell construction of a phase transition, in a Gibbs construction a mixed phase is present in the stars interior, where both phases co-exist. In the mixed phase transition region each phase has a charge; only the overall electrical charge density vanishes. In the mixed phase, the pressure of the hadronic matter has to be equal to the pressure of the quark phase, whereas the particle and energy densities differ. For a summary, please look at the following transparencies: