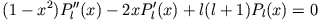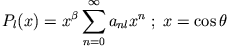Elektrostatik - Geladene Metallkörper

1. Berechne das Potential auf einer ladungsfreien Kreisebene mit Radius 1. Das Potential am Rand der Kreisebene ist , .




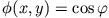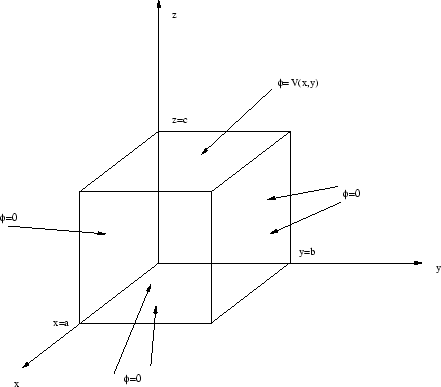
2. Löse die Laplace-Gleichung in kartesischen Koordinaten durch einen Separationsansatz und diskutiere damit das Problem eines rechteckigen Kastens mit den Kantenlängen 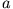, 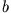und 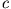in x-, y- und z-Richtung.
   
   Alle Flächen sollen das Potential Null besitzen außer der Fläche 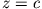, die das Potential 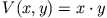hat.





3. a)

   Diskutiere den Separationsansatz der Laplace-Gleichung in Kugelkoordinaten und löse die Legendre-Differentialgleichung

   

   mit Hilfe der Reihenentwicklung

   

   b)

   Zeige, dass die Legendre-Polynome orthogonal zueinander sind.





4. Berechne das Potential einer Kugel vom Radius 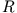mit der Ladungsverteilung
   
   
   durch Lösung der Poisson- bzw. Laplace-Gleichung.




5. Die Quellen eines elektrischen Feldes sind axialsymmetrisch verteilt. In der Nähe der Symmetrieachse des Systems gibt es keine Quellen des Feldes. Berechne das Potential 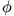in der Nähe der Symmetrieachse.




6. Die Oberfläche einer Kugel mit dem Radius 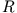habe die Ladungsdichte 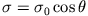. Man bestimme das Potential 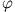des elektrischen Feldes unter der Anwendung der Multipolentwicklung in Kugelkoordinaten.




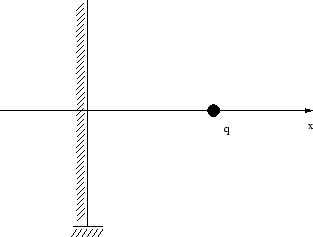
7. Warum kann man das Problem 'Punktladung 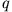vor geerdeter Ebene' durch die Bildpunktmethode lösen?
   
   Bestimme und diskutiere die Ladungsverteilung auf der Ebene.




8. Erfinde eine Ladungsverteilung, die nur ein Quadrupolmoment erzeugt. Beschreibe die Ladungsverteilung im Detail.




9. Im sog. Kollektivmodell des Atomkerns wird die Kernoberfläche beschrieben durch
   
   Berechne das Quadrupolmoment eines gleichförmig geladenen Köpers mit dieser Oberfläche bis zu Gliedern 1. Ordnung in .




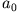10. Bestimme das Potential eines gleichförmig geladenen dünnen Kreisringes unter Benutzung der Multipolentwicklung in Kugelkoordinaten. Die Ladung des Ringes ist 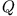, sein Radius .




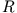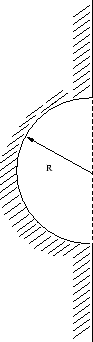
11. Berechne das Potential für das folgende Problem: In einer Metallfläche, die auf dem Potential Null gehalten wird, ist eine halbkugelförmige Delle vom Radius .
    
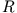    Auf der Leiterfläche ist die Ladung so aufgetragen, dass das elektrische Feld für große Entfernungen von der Oberfläche homogen ist. Bestimme auch Feld und Ladungsverteilung auf der Fläche. Welches Problem erfüllt die gleichen Randbedingungen?

Druckversion der Aufgaben
Druckversion der Lösungen