Der Laplace-Operator in Zylinderkoordinaten lautet:
Setzt man den Separationsansatz
in die Laplace-Gleichung
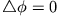 ein, so erhält man
ein, so erhält man
Multiplikation mit
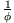 separiert die Laplace-Gleichung in die Differentialgleichungen
separiert die Laplace-Gleichung in die Differentialgleichungen
Die Lösung der ersten Gleichung ist der harmonische Oszillator
Da aber das Potential axialsymmetrisch ist, muss für jedes
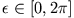 gelten
gelten
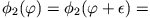 const. const.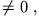 |
|
was nur für 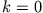 erfüllt werden kann. D.h. es bleibt
erfüllt werden kann. D.h. es bleibt
zu lösen.
Für das Potential auf der Symmetrieachse gilt
Setze die Lösung in Form einer Potenzreihe in 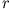 an
an
so erhält man zusammen mit der obigen Beziehung
Setzt man den Potenzreihenansatz in die Differentialgleichung ein und fordert, dass 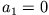 , so erhält man eine Rekursionsformel für die
, so erhält man eine Rekursionsformel für die
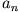
Beispiel:
Daraus folgt
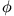 ist das Potential im ladungsfreien Raum um die Symmetrieachse.
ist das Potential im ladungsfreien Raum um die Symmetrieachse.
M.Keim, H.J. Lüdde