1

Zu lösen ist die Laplace-Gleichung in zwei Dimensionen

Um die Randbedingung möglichst einfach angeben zu können, schreibt man diese Gleichung in ebene Polarkoordinaten 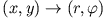um

mit der Randbedingung

Zur Separation der Variablen setze

in die Differentialgleichung ein

Division durch 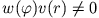und Multiplikation mit 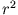ergibt

und es folgen die beiden Gleichungen

Die allgemeine Lösung der ersten Gleichung ist

Damit 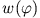eindeutig ist, muss gelten

Koeffizientenvergleich ergibt

Die zweite Gleichung ist eine Differentialgleichung vom Euler-Typ. Wähle als Ansatz

Einsetzen liefert

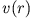soll für 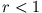beschränkt sein, insbesondere für 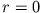, d.h. 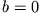. Damit hat man als Gesamtlösung

Aus der Randbedingung erhält man