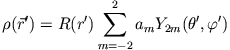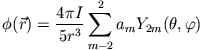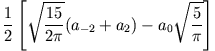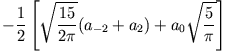Ein Quadrupolfeld hat die Form
mit
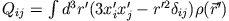, dem Quadrupolmoment-Tensor. Im folgenden wird nur das Feld außerhalb der
Ladungsverteilung betrachtet; man kann also allgemein schreiben
mit den Multipolmomenten
In dieser Summe dürfen nur die Quadrupolmomente Beiträge zum Potential liefern, daher kann man auf Grund der Orthogonalitätsrelation der
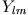für die Ladungsverteilung den Ansatz
machen. Damit erhält man für die Quadrupolmomente (mit
):
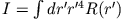alle anderen Multipolmomente verschwinden. Somit gilt
Drückt man die Kugelflächenfunktionen durch die kartesischen Komponenten von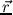 
aus, so lautet
und nach weiterer Umformung
Da
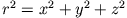, folgt für die Elemente des Quadrupolmoment-Tensors:
Man sieht sofort, dass die Summe der Diagonalglieder des Tensors verschwindet; der Tensor also 5 unabhängige Komponenten hat. Es ist
sofort einzusehen, dass in einem solchen Quadrupolfeld die Gesamtladung verschwindet
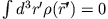und die Ladungsverteilung
ein verschwindendes Dipolmoment erzeugt
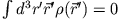. Das Quadrupolfeld ist ellipsoidförmig.
M.Keim, H.J. Lüdde
