- a)
- Die Laplace-Gleichung lautet in Kugelkoordinaten:
Setzt man den Produktansatz
in die obige Differentialgleichung ein, so erhält man
Multiplikation mit
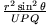 ergibt
ergibt
Ähnlich wie in der vorhergehenden Aufgabe, wählt man
Einsetzen dieser Lösung und Division durch
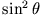 ergibt die beiden Differentialgleichungen für
ergibt die beiden Differentialgleichungen für 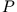 und
und 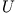
Substituiert man
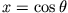 , so erhält man aus der ersten Gleichung die verallgemeinerte Legendre-Differentialgleichung
, so erhält man aus der ersten Gleichung die verallgemeinerte Legendre-Differentialgleichung
die für 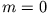 in die Legendre'sche Differentialgleichung übergeht:
in die Legendre'sche Differentialgleichung übergeht:
Einsetzen der Reihenentwicklung für 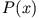 ergibt:
ergibt:
Damit diese Summe verschwindet, muss der Koeffizient jeder Potenz von 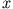 verschwinden. Betrachten wir die jeweils niedrigste Potenz in
verschwinden. Betrachten wir die jeweils niedrigste Potenz in
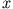 , so gilt für
, so gilt für
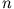 |
 |
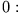 wenn wenn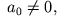 dann ist dann ist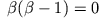 |
|
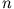 |
 |
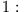 wenn wenn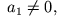 dann ist dann ist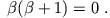 |
|
Im allgemeinen Fall ergibt Koeffizientenvergleich die Rekursionsformel
Man sieht leicht, dass die beiden vorherigen Beziehungen äquivalent sind. Man braucht also nur entweder 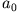 oder
oder 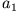 ungleich Null zu
wählen. Im ersten Fall hat man die Wurzeln
ungleich Null zu
wählen. Im ersten Fall hat man die Wurzeln 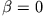 und
und 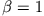 , die eine gerade (
, die eine gerade (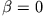 ) bzw. ungerade (
) bzw. ungerade (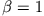 )
Potenzreihe in
)
Potenzreihe in 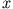 liefern. Da man eine beschränkte Lösung für
liefern. Da man eine beschränkte Lösung für
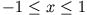 sucht, soll die Potenzreihe abbrechen. Da
sucht, soll die Potenzreihe abbrechen. Da 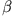 und
und 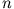 ganze Zahlen
ganze Zahlen  sind, bricht die Rekursionsformel nur ab, wenn auch
sind, bricht die Rekursionsformel nur ab, wenn auch 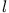 eine ganze, positive Zahl ist. Wenn
eine ganze, positive Zahl ist. Wenn 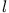 gerade (ungerade),
bricht nur die
gerade (ungerade),
bricht nur die 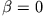 (
(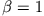 ) Reihe ab. Die so erhaltenen Polynome in
) Reihe ab. Die so erhaltenen Polynome in 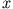 werden derart normiert, dass sie für
werden derart normiert, dass sie für 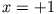 gleich eins
sind. Die normierten Polynome heißen Legendre-Polynome der Ordnung
gleich eins
sind. Die normierten Polynome heißen Legendre-Polynome der Ordnung 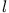 .
.
- b)
- Die Legendre-Polynome erfüllen die Differentialgleichung
Multiplikation mit 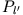 und Integration über
und Integration über 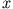
Partielle Integration des ersten Terms ergibt
Vertauscht man in dieser Gleichung 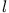 mit
mit 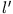 und subtrahiert die neue von der alten Gleichung, so ergibt sich:
und subtrahiert die neue von der alten Gleichung, so ergibt sich:
Falls 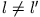 muss das Integral verschwinden, damit die Gleichung erfüllt ist. Im Fall
muss das Integral verschwinden, damit die Gleichung erfüllt ist. Im Fall 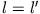 kann man sofort sehen, dass das Integral
endlich ist. Damit ist die Orthogonalität der
kann man sofort sehen, dass das Integral
endlich ist. Damit ist die Orthogonalität der 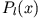 bewiesen.
bewiesen.
M.Keim, H.J. Lüdde