Laplace-Gleichung in kartesischen Koordinaten:
Separationsansatz:
Damit liefert die Laplace-Gleichung
Damit diese Gleichung für beliebige Werte der unabhängigen Variablen gilt, muss jeder der 3 Terme für sich konstant sein:
mit
Angenommen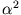 
und 
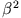seien positiv, dann besitzen die obigen 3 Differentialgleichungen die Lösungen
Im allgemeinen kann
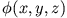nun als Produkt von Linearkombinationen der
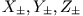dargestellt werden. Die Konstanten
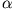und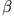 
werden durch die Randbedingungen eines speziellen Problems bestimmt. Dies soll beispielhaft an Hand des rechteckigen
Kastens geschehen. In diesem Fall erfüllen
und
die Bedingung, dass
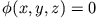für
.
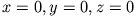Damit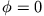 
bei 
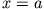und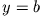 
, muss gelten:
Folglich kann man das Potential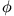 
als Linearkombination der 'partiellen Potentiale'
darstellen:
Da
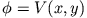bei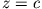 
, kann man mit Hilfe dieser Randbedingung die Entwicklungskoeffizienten 
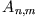bestimmen; es ist nämlich
Dies ist eine doppelte Fourierreihe für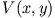 
, so dass die 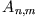gegeben sind als
Integration liefert:
M.Keim, H.J. Lüdde
