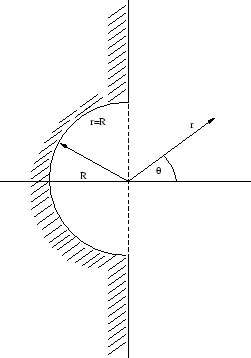
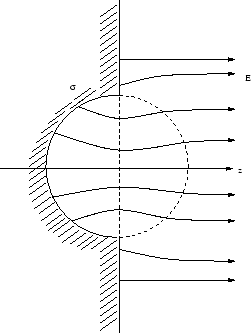
Stellt man eine ungeladene, leitende Kugel in ein homogenes elektrisches Feld, so lautet das Potential
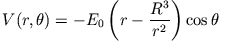 (siehe Vorlesung) (siehe Vorlesung) |
|
Dieses Potential erfüllt die gleichen Randbedingungen, wie sie im vorgegebenen Problem vorliegen. Beweis in Polarkoordinaten:
- a)
-
Dies ist die Zerlegung des Vektors
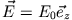 weil
weil
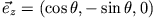 . Somit ist das Feld in großer
Entfernung homogen.
. Somit ist das Feld in großer
Entfernung homogen.
- b)
-
Die Lösung erfüllt also die Randbedingung, dass das Potential auf der Leiteroberfläche Null ist.
- 1)
- Auf der ebenen Fläche das Leiters berechnet sich die Oberflächenladungsdichte zu
Dazu transformiert man das Potential in kartesische Koordinaten:
und es folgt
d.h. bei großem Abstand von der Delle wird
Ansonsten ist
 .
.
- 2)
- Die Oberflächenladung auf der Delle beträgt
Also
In der Delle gilt
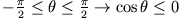 und
und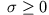 .
Somit hat das elektrische Feld etwa den folgenden Verlauf:
.
Somit hat das elektrische Feld etwa den folgenden Verlauf:
M.Keim, H.J. Lüdde