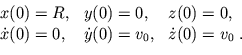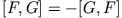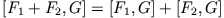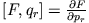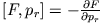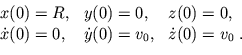Aufgaben - Kapitel 8

1. Diskutiere die Bewegung des Kurbelmechanismus.




2. Ein Teilchen bewegt sich auf der Oberfläche eines Zylinders unter der Einwirkung der Kraft 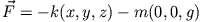. Bestimme die Bewegung für die Anfangsbedingungen
   
   





3. Ein Massenpunkt bewegt sich im Schwerefeld der Erde in einer kugelförmigen Schale (Kugelpendel). Bestimme die Lagrangefunktion und die Bewegungsgleichung. Was sind günstige generalisierte Koordinaten? Wo steckt der Flächensatz und wie ist hier die geometrische Deutung?




4. Bestimme die Lagrangefunktion und die Bewegungsgleichung für das Zykloidenpendel. Parameterdarstellung der Bahn:
   
   
   Die Pendellänge beträgt 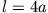. (Benutze )




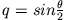5. Bestimme die Bewegungsgleichung des Doppelpendels für kleine Ausschläge beider Massen.




6. Vergleiche die Hamiltonschen Bewegungsgleichungen mit den Lagrangegleichungen 2. Art.

   a)

   Worin bestehen Unterschiede bzw. Vor- und Nachteile?

   b)

   Welche Aussagen können über die Hamiltonfunktion gemacht werden?





7. Gegeben sind die Funktionen F und G, die nur von den Koordinaten 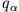, den Impulsen 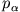und der Zeit 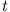abhängen. Als Poissonklammer von F und G definiert man:
   
   
   Beweisen Sie, dass:

   a)

   

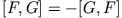
   b)

   

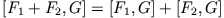
   c)

   

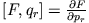
   d)

   

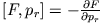
Druckversion der Aufgaben
Druckversion der Lösungen