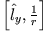- a)
- Berechne Dichte
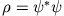
und Stromdichte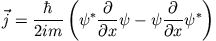
des Wellenpaketes und interpretiere das Ergebnis. - b)
- Wie muss man den Normierungsfaktor
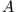 wählen, wenn
wählen, wenn 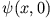 ein einzelnes freies Teilchen beschreiben soll?
ein einzelnes freies Teilchen beschreiben soll?
- c)
- Bestimme die Impulsverteilung des Wellenpaketes und diskutiere an diesem Beispiel die Unschärferelation.
- d)
- Berechne die Zeitentwicklung des Wellenpaketes und zeige, dass es mit der Zeit zerfließt.
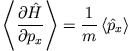 |
|||
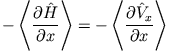 |
mit dem Hamilton-Operator
- a)
-
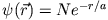
- b)
-
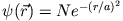
- a)
- Normieren Sie
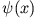 .
.
- b)
- Berechnen Sie die Erwartungswerte der Operatoren
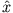 und
und 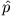 .
.
- c)
- Zeigen Sie, dass gilt
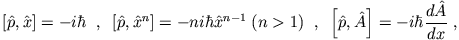
wobei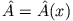 eine differenzierbare Funktion von
eine differenzierbare Funktion von 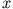 ist.
ist.
- a)
- Zeigen Sie die Gültigkeit der Kontinuitätsgleichung
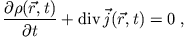
mit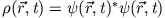 und
und
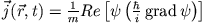 .
Interpretieren Sie den Erhaltungssatz! Kennen Sie eine andere Theorie, in der eine Kontinuitätsgleichung gilt?
.
Interpretieren Sie den Erhaltungssatz! Kennen Sie eine andere Theorie, in der eine Kontinuitätsgleichung gilt?
- b)
- Betrachten Sie die Wellenfunktion
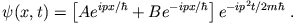
Finden Sie den zugehörigen Wahrscheinlichkeitsstrom und interpretieren Sie ihn. - c)
- Zeigen Sie, dass für ein eindimensionales, quadratintegrables Wellenpaket gilt
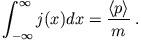
- a)
-
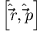
- b)
-
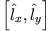
- c)
-
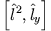
- d)
-