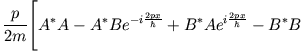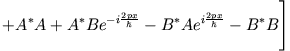- a)
- Die Schrödinger-Gleichung ist
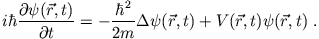 |
(1) |
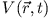 ist hier reell, das komplex Konjugierte von (1) ist
ist hier reell, das komplex Konjugierte von (1) ist
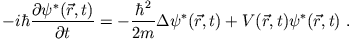 |
(2) |
Nach Definition ist
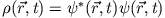 , daraus folgt
, daraus folgt
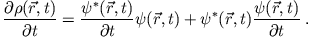 |
(3) |
Wir setzen (1) und (2) in (3) ein:
Gleichung (4) können wir auch schreiben als
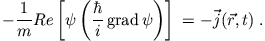 |
(5) |
Jetzt benutzen wir
und erhalten aus (5)
Durch den Vergleich mit (4) erhält man schließlich die Kontinuitätsgleichung
- b)
- Wellenfunktion:
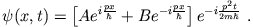
Stromdichte:
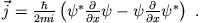
Die ,,Zutaten``der Rechnung sind gegeben durch
Damit folgt für die Stromdichte nach kurzer Rechnung
Zur Interpretation:
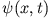 ist die Superposition von zwei Teilchenströmen, die sich in entgegengesetzte Richtungen bewegen. Jeder der Teilchenströme
ist konstant und zeitunabhängig in seiner Größe. Der Term
ist die Superposition von zwei Teilchenströmen, die sich in entgegengesetzte Richtungen bewegen. Jeder der Teilchenströme
ist konstant und zeitunabhängig in seiner Größe. Der Term
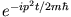 zeigt, dass die Teilchen die Energie
zeigt, dass die Teilchen die Energie
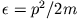 haben.
Die Amplituden der Teilchenströme sind
haben.
Die Amplituden der Teilchenströme sind 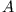 und
und 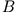 .
.
- c)
- Nach Voraussetzung ist das Integral
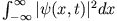 endlich, d.h.
endlich, d.h.
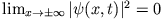 . Zu berechnen ist
. Zu berechnen ist
Partielle Integration ergibt:
Einsetzen führt schließlich auf
M. Keim, H.J. Lüdde