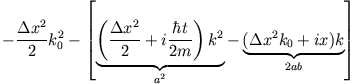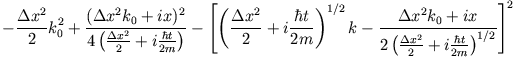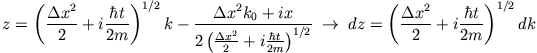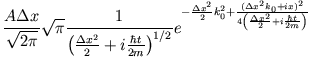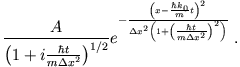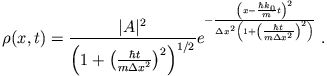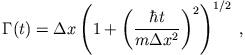1

a)

Die quantenmechanische Dichte 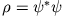ist im Ortsraum ein Maß für die Wahrscheinlichkeit, ein Teilchen am Ort 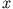zu finden.

In unserem Falle (vergleiche Eigenschaften der Gauss-Verteilung) befindet sich das Teilchen mit hoher Wahrscheinlichkeit im Bereich .
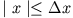Die Stromdichte 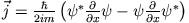ist ein Maß für den Wahrscheinlichkeitsfluss und ist mit der Dichte über die Kontinuitätsgleichung verknüpft

wenn man Teilchenzahlerhaltung annimmt (im relativistischen Fall nicht notwendig der Fall).

Die klassische Stromdichte ist definiert als 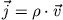, so dass man 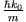als die Geschwindigkeit des Wellenpaketes auffassen kann (Gruppengeschwindigkeit).

b)

Soll 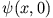ein einziges Teilchen beschreiben, muss die Wahrscheinlichkeit, irgendein Teilchen irgendwo im Raum zu finden, 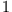sein, d.h.

Einsetzen und Verwendung des Fehlerintegrals liefert mit der Substitution
:

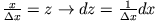c)

Die Impulsverteilung erhält man durch Fourier-Transformation von

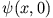
Lösung des Integrals durch quadratische Ergänzung des Exponenten und Anwendung des Fehlerintegrals:

Substitution:

Die Wahrscheinlichkeit, dass das Wellenpaket den Impuls 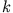besitzt, ist dann

Die Impulsverteilung des Wellenpaketes ist also ebenfalls eine Gauss-Verteilung, allerdings mit der Breite 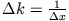bzw. 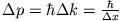. Multipliziert man Orts- und Impulsunschärfe, erhält man für dieses Beispiel

also die exakte Erfüllung der Unschärferelation. Anschaulich sieht man: Je enger die Ortsraumverteilung ist 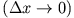, desto unschärfer wird die Impulsverteilung .

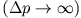d)

Die Wellenfunktion zu irgendeinem Zeitpunkt erhält man aus

Einsetzen der Impulsverteilung 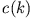liefert

Der Exponent ist auch hier eine quadratische Form in 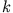, so dass das Integral auf das Fehlerintegral zurückführbar ist. Quadratische Ergänzung des Exponenten:

Substituiere

daraus folgt

Für die Dichte 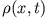erhält man

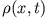ist ebenfalls eine Gauss-Kurve mit dem Maximum an der Stelle 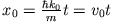( 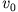Gruppengeschwindigkeit siehe Aufgabenteil a)), d.h. das Maximum breitet sich mit der geschwindigkeit 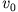in x-Richtung aus. Die Breite der Gauss-Kurve ist offenbar zeitabhängig

d.h. das Wellenpaket fließt mit der Zeit auseinander, der Ort des Teilchens wird immer unschärfer. Wie kann man also einen Teilchenstrahl mit scharfem Impuls präparieren?