Aufgaben - Kapitel 5
- Ein Satellit umkreist die Erde in der Äquatorebene. In welcher
Höhe über der Erdoberfläche muss er umlaufen, damit er stets über dem
gleichen Punkt bleibt (geostationäre Bahn)?

- Die Beschleunigung eines Massenpunktes ist durch
gegeben. Bestimme die Bahnkurve, wenn die Anfangsbedingungen
lauten:
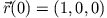 und
und
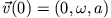 .
Beschreibe die Bahnkurve und ihre Eigenschaften.
.
Beschreibe die Bahnkurve und ihre Eigenschaften.

- Berechne die Fläche der durch
definierten Lissajous-Figur. Wie sieht sie aus und gilt in diesem
Fall der Flächensatz?

- Zeige, dass sich eine Masse in einem zentralen Kraftfeld
auf einer ebenen Bahn bewegt.

- Ein Teilchen bewegt sich im Kraftfeld
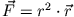 ,
wobei
,
wobei 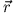 sein Positionsvektor ist.
Zeige, dass der Drehimpuls eine Erhaltungsgröße ist.
sein Positionsvektor ist.
Zeige, dass der Drehimpuls eine Erhaltungsgröße ist.

- Eine zeitlich veränderliche Kraft
wirkt auf einen Massenpunkt (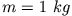 ) ein. Berechne die Arbeit, die die Kraft an dem Massenpunkt leistet,
wenn sie während des Zeitintervalles
) ein. Berechne die Arbeit, die die Kraft an dem Massenpunkt leistet,
wenn sie während des Zeitintervalles
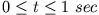 einwirkt.
Die Anfangsbedingungen für die Bewegung des Massenpunktes sind:
einwirkt.
Die Anfangsbedingungen für die Bewegung des Massenpunktes sind:

- Zwei Massen
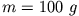 und
und 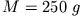 sind durch ein
Seil über eine Rolle verbunden.
sind durch ein
Seil über eine Rolle verbunden.
- a)
- Stelle die Bewegungsgleichungen der Massen auf.
- b)
- Berechne die Kräfte, die auf die beiden Massen
wirken.
- c)
- Zeige, dass aus den Bewegungsgleichungen der Energieerhaltungssatz
folgt.

- In einer Höhe
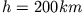 über dem Äquator wird ein künstlicher Satellit in horizontaler Richtung (
über dem Äquator wird ein künstlicher Satellit in horizontaler Richtung (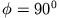 )
nach Osten mit einer Geschwindigkeit
)
nach Osten mit einer Geschwindigkeit 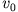 (relativ zur Erdoberfläche) gestartet.
(relativ zur Erdoberfläche) gestartet.
- a)
- Wie groß muss
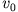 gewählt werden, damit der Satellit eine Kreisbahn bzw. eine Parabelbahn durchläuft?
gewählt werden, damit der Satellit eine Kreisbahn bzw. eine Parabelbahn durchläuft?
- b)
- Welche Folge hätte ein Fehler von
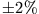 im Höhenwinkel
im Höhenwinkel 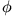 beim Abschuss mit der Kreisbahngeschwindigkeit?
Bedenken Sie, dass ein veränderter Höhenwinkel einen veränderten Drehimpuls bedingt.
beim Abschuss mit der Kreisbahngeschwindigkeit?
Bedenken Sie, dass ein veränderter Höhenwinkel einen veränderten Drehimpuls bedingt.
Hinweis : Benutzen Sie folgende Relationen :
Die numerische Exzentrizität der Satellitenbahn im Zentralkraftfeld der Erde ist, wenn man die reduzierte
Masse
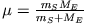 wegen
wegen 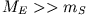 durch
durch 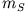 approximiert:
approximiert:
Dabei ist 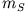 die Satellitenmasse,
die Satellitenmasse, 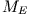 die Erdmasse,
die Erdmasse, 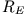 der Erdradius, E die Energie
der Erdradius, E die Energie
und L der Drehimpuls

 Druckversion der Aufgaben
Druckversion der Aufgaben
 Druckversion der Lösungen
Druckversion der Lösungen
H.J. Lüdde, M. Keim
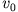 gewählt werden, damit der Satellit eine Kreisbahn bzw. eine Parabelbahn durchläuft?
gewählt werden, damit der Satellit eine Kreisbahn bzw. eine Parabelbahn durchläuft?
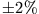 im Höhenwinkel
im Höhenwinkel 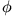 beim Abschuss mit der Kreisbahngeschwindigkeit?
Bedenken Sie, dass ein veränderter Höhenwinkel einen veränderten Drehimpuls bedingt.
beim Abschuss mit der Kreisbahngeschwindigkeit?
Bedenken Sie, dass ein veränderter Höhenwinkel einen veränderten Drehimpuls bedingt.