Elektrostatik - Ladungen in materiefreiem Raum
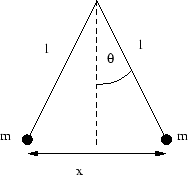
- Zwei gleiche Punktladungen (Ladung
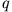 , Masse
, Masse 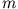 ) hängen an Fäden der Länge
) hängen an Fäden der Länge 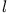 .
Berechnen Sie den Abstand
.
Berechnen Sie den Abstand 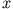 , der sich unter dem Einfluss von Gravitation und
elektrischer Abstoßung einstellt (unter der Annahme kleiner Winkel
, der sich unter dem Einfluss von Gravitation und
elektrischer Abstoßung einstellt (unter der Annahme kleiner Winkel 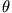 , also
, also
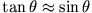 ).
).
Wie groß muss 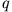 sein, damit
sein, damit 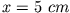 für
für 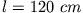 und
und 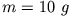 ist?
ist?

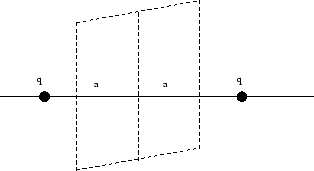
- Zwei positive Ladungen
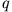 haben den Abstand
haben den Abstand 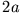 . Eine Testladung wird in die Trennebene zwischen die beiden Ladungen gebracht.
Berechne die Kurve in dieser Ebene, für die die Kraft auf die Testladung ein Maximum hat. In welcher Richtung zeigt
der Kraftvektor, wenn die Testladung positiv ist?
. Eine Testladung wird in die Trennebene zwischen die beiden Ladungen gebracht.
Berechne die Kurve in dieser Ebene, für die die Kraft auf die Testladung ein Maximum hat. In welcher Richtung zeigt
der Kraftvektor, wenn die Testladung positiv ist?

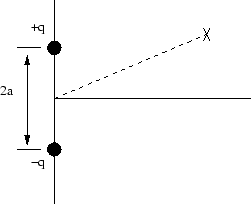
- Berechne das Feld (
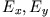 ) eines Dipols (Dipolmoment
) eines Dipols (Dipolmoment 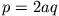 ) für einen beliebigen Punkt in der x-y-Ebene unter der Annahme
) für einen beliebigen Punkt in der x-y-Ebene unter der Annahme
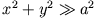 .
.

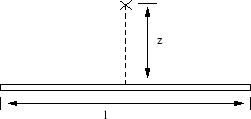
- Ein dünner nichtleitender Stab der Länge
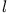 trägt eine uniforme Ladungsverteilung (
trägt eine uniforme Ladungsverteilung (
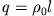 ).
Berechne das
elektrische Feld in dem angegebenen Punkt (Abstand
).
Berechne das
elektrische Feld in dem angegebenen Punkt (Abstand 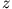 von der Mitte des Stabes).
von der Mitte des Stabes).

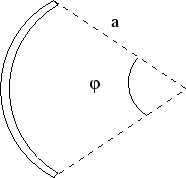
- Der Stab aus Aufgabe 4 bildet einen Kreisbogen mit dem Radius
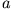 und dem Winkel
und dem Winkel 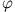 .
Berechne das elektrische Feld in dem
Kreismittelpunkt als Funktion von
.
Berechne das elektrische Feld in dem
Kreismittelpunkt als Funktion von 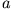 ,
, 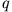 und
und 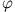 .
.

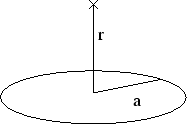
- Eine d ünne Kreisscheibe (Radius
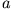 ) ist uniform geladen. Die Ladungsdichte ist
) ist uniform geladen. Die Ladungsdichte ist
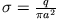 .
Berechne das elektrische Feld auf der Achse der Scheibe für den Abstand
.
Berechne das elektrische Feld auf der Achse der Scheibe für den Abstand 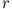 .
.

- Berechne das Feld einer Kugel (Radius
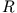 ) mit den Ladungsverteilungen
) mit den Ladungsverteilungen
- a)
-
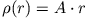
- b)
-
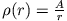 .
.

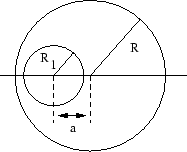
- Aus einer kugelsymmetrischen homogenen Raumladungsverteilung vom Radius
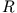 wird eine kleinere Kugel vom Radius
wird eine kleinere Kugel vom Radius 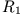 herausgeschnitten.
Der Abstand der Zentren beider Kugeln ist
herausgeschnitten.
Der Abstand der Zentren beider Kugeln ist 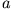 . Berechne das Feld im Hohlraum.
. Berechne das Feld im Hohlraum.

- Berechne die Kapazität eines Zylinderkondensators der Länge
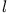 und der Radien
und der Radien 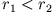 . Die Kapazität ist definiert durch
. Die Kapazität ist definiert durch
worin 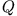 die Gesamtladung des Kondensators und
die Gesamtladung des Kondensators und 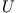 die Spannung (Potentialdifferenz!) zwischen den Kondensatorflächen
bedeuten.
die Spannung (Potentialdifferenz!) zwischen den Kondensatorflächen
bedeuten.

- Die Ladung des Elektrons ist im Wasserstoffatom (Grundzustand) mit der Dichte
verteilt, wobei
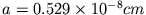 den Bohrschen Radius und
den Bohrschen Radius und
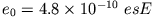 die
Elementarladung bedeuten. Bestimmen Sie die elektrische Feldstärke der Elektronenladung und die elektrische
Gesamtfeldstärke im Atom unter der Annahme, dass die Protonenladung im
Koordinatenursprung konzentriert ist.
die
Elementarladung bedeuten. Bestimmen Sie die elektrische Feldstärke der Elektronenladung und die elektrische
Gesamtfeldstärke im Atom unter der Annahme, dass die Protonenladung im
Koordinatenursprung konzentriert ist.

- Berechne das Potential eines langgestreckten Quadrupolsfür große Abstände
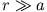 .
.

- Welche Ladungsverteilung erzeugt ein Potential, das in Kugelkoordinaten die Form
hat, wobei 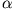 und
und 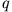 Konstanten sind?
Konstanten sind?

 Druckversion der Aufgaben
Druckversion der Aufgaben
 Druckversion der Lösungen
Druckversion der Lösungen
M.Keim, H.J. Lüdde
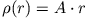
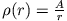 .
.