Next: Totalreflexion () Up: Simulation von Schrödinger-Wellenpaketen Previous: Freie Teilchen
Als einfachstes Beispiel betrachten wir nun eine Potentialschwelle der Form
Die Konstanten unterliegen nun der Einschränkung, daß die Lösungen
zweimal differenzierbar sein müssen. Es müssen daher ![]() und
und
![]() bei
bei ![]() stetig sein. Zusammen mit der
Normierungsvorschrift (37) ergeben sich aus diesen
Stetigkeitsbedingungen für die Koeffizienten
stetig sein. Zusammen mit der
Normierungsvorschrift (37) ergeben sich aus diesen
Stetigkeitsbedingungen für die Koeffizienten
Ein erstes physikalisches Verständnis für diese Wellenfunktionen
ergibt eine Betrachtung, die analog zur Behandlung der realistischeren
Streuprozesse im dreidimensionalen Raum ist. Dabei interessiert man sich
nur für das asymptotische Verhalten der Teilchen, d.h. wenn sie sich
weit weg von der Schwelle bei ![]() aufhalten.
aufhalten.
Dabei müssen wir bedenken, daß die Wellenfunktionen ![]() keine
,,echten`` Zustände repräsentieren, da sie nicht
quadratintegrabel und somit nicht normierbar sind. Sie können aber als
Grenzfall von echten Zuständen gedeutet werden, nämlich gerade solche,
wo
keine
,,echten`` Zustände repräsentieren, da sie nicht
quadratintegrabel und somit nicht normierbar sind. Sie können aber als
Grenzfall von echten Zuständen gedeutet werden, nämlich gerade solche,
wo
Stellen wir den Detektor irgendwo links weit weg von der Schwelle auf,
wird er sowohl die einlaufenden als auch die an der Schwelle
reflektierten Teilchen messen. Ein sehr weit rechts positionierter
Detektor wird die Teilchen erfassen, die die Schwelle überwinden. Wir
können also im Prinzip die auf den Strom der einlaufenden Teilchen
normierten Wahrscheinlichkeiten messen, daß ein Teilchen, das mit einer
wohldefinierten Energie ![]() sehr weit links von der Schwelle losläuft,
irgendwann reflektiert wird bzw. die Schwelle überwindet und sehr weit
weg nach rechts läuft. Diese relativen Ströme bezeichnen wir als
Reflexions- bzw. Transmissionskoeffizienten2. Gemäß (24) sind für
unsere Schwelle die Koeffizienten durch
sehr weit links von der Schwelle losläuft,
irgendwann reflektiert wird bzw. die Schwelle überwindet und sehr weit
weg nach rechts läuft. Diese relativen Ströme bezeichnen wir als
Reflexions- bzw. Transmissionskoeffizienten2. Gemäß (24) sind für
unsere Schwelle die Koeffizienten durch
Wegen der Stromerhaltung gilt
Für unsere Movies wollen wir die Wahrscheinlichkeitsdichten für ein
anfangs bei ![]() konzentriertes nach rechts auf die
Potentialschwelle zulaufendes Wellenpaket als Funktion der Zeit
simulieren. Dies erreichen wir, indem wir
konzentriertes nach rechts auf die
Potentialschwelle zulaufendes Wellenpaket als Funktion der Zeit
simulieren. Dies erreichen wir, indem wir ![]() gemäß
(42) wählen.
gemäß
(42) wählen.
Dies entspricht physikalisch der Situation, daß wir einen Strom von
jeweils einem einzelnen recht gut lokalisierten Teilchen beobachten und
an jedem Ort ![]() einen Detektor aufstellen, der jedesmal die Zeit
erfaßt, die nach dem Losschicken des Teilchens vergangen ist, wann er
das Teilchen registriert. Dann kann man wieder die relativen
Häufigkeiten als Funktion der Zeit erfassen, und erhält dann genau die
Wahrscheinlichkeitsverteilungen, die wir im folgenden in den Movies
zeigen wollen.
einen Detektor aufstellen, der jedesmal die Zeit
erfaßt, die nach dem Losschicken des Teilchens vergangen ist, wann er
das Teilchen registriert. Dann kann man wieder die relativen
Häufigkeiten als Funktion der Zeit erfassen, und erhält dann genau die
Wahrscheinlichkeitsverteilungen, die wir im folgenden in den Movies
zeigen wollen.
Dabei ist es wichtig zu bemerken, daß aufgrund der Heisenbergschen Unschärferelation für Ort und Impuls
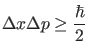 |
(51) |
| (52) |