Freie Teilchen

Das freie Teilchen, also der Fall läßt sich einfacher mit Hilfe von Impulseigenzuständen behandeln. Wir haben auf den Aufgabenblättern 1 und 2 das Gaußsche Wellenpaket für freie Teilchen ausführlich behandelt. Für unsere Simulationen wollen wir dieses Wellenpaket für $x \ll 0$ als Anfangszustand konstruieren. Wir arbeiten aber wie oben betont in dem Unterraum mit nur nach $x \rightarrow \infty$ hin auslaufenden Wellen. Die entsprechende auf $\delta(E-E')$ ,,normierte” Energieeigenfunktion ist nach den obigen allgemeinen Betrachtungen also durch

$\displaystyle \psi_E(x)=\sqrt{\frac{m}{2 \pi \hbar k}} \exp(\ii k x)$ mit $\displaystyle \quad k=\frac{\sqrt{2 m E}}{\hbar}$

(40)

gegeben.

Wir verwenden nun folgende Näherung. Im Impulsraum (geschrieben mit Wellenzahlen $k=p/\hbar$ ) lautet das Anfangswellenpaket, das wir allerdings nicht um herum plazieren wollen, sondern bei $x_0 \ll 0$ :

$\displaystyle \tilde{\psi}_0(k)=\frac{1}{(2 \pi \alpha)^{1/4}} \exp \left [-\frac{(k-k_0)^2}{4 \alpha} -\ii k x_0 \right ].$

(41)

Für unsere Rechnungen verwenden wir stattdessen den folgenden Anfangszustand in der Energiedarstellung

$\displaystyle c_E=\sqrt{\frac{m}{\hbar k}}[\tilde{\phi}_0(k)+\tilde{\phi}_0(-k)]$ mit $\displaystyle \quad k=\frac{\sqrt{2 m E}}{\hbar}.$

(42)

Zur Berechnung der zeitabhängigen Lösung integrieren wir diese Anfangswellenfunktion gem. (39). Da hier keine gebundenen Zustände existieren, ist

$\displaystyle \Psi(x,t)=\int_{0}^{\infty} \dd E \, c_E \, \psi_E(x) \exp \left (-\frac{\ii E t}{\hbar} \right).$

(43)

Dies ist für nicht zu breite Impulsverteilungen (also nicht zu große $\alpha$ ) eine sehr guter Näherung für das Gaußsche Wellenpaket, wie das unten gezeigte Movie auch zeigt.

Zur Herstellung der Movies wird dieses Integral mit einer einfachen adaptiven Trapez-Simpson-Quadratur numerisch ausgewertet. Dabei ist es wegen der Singularität des Anfangszustandes (42) bei allerdings von Vorteil, nach zu integrieren. Es ist

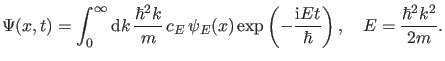$\displaystyle \Psi(x,t)=\int_{0}^{\infty} \dd k \, \frac{\hbar^2 k}{m} \, c_E \... ...(x) \exp \left (-\frac{\ii E t}{\hbar} \right), \quad E=\frac{\hbar^2 k^2}{2m}.$

(44)

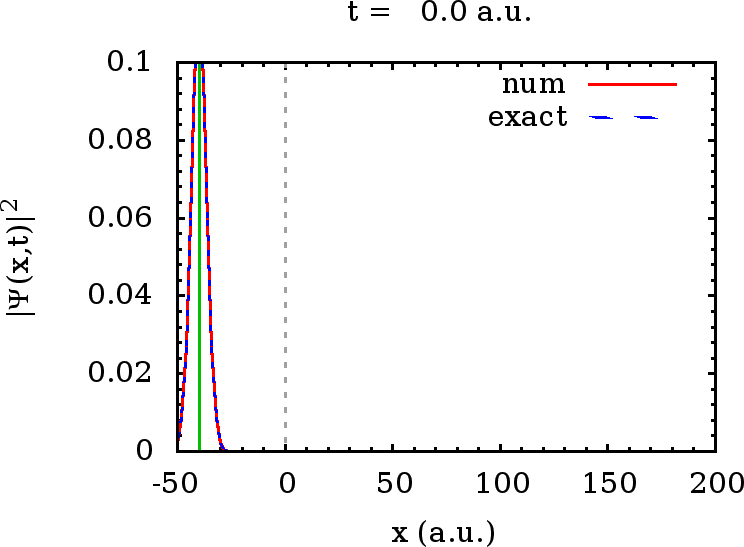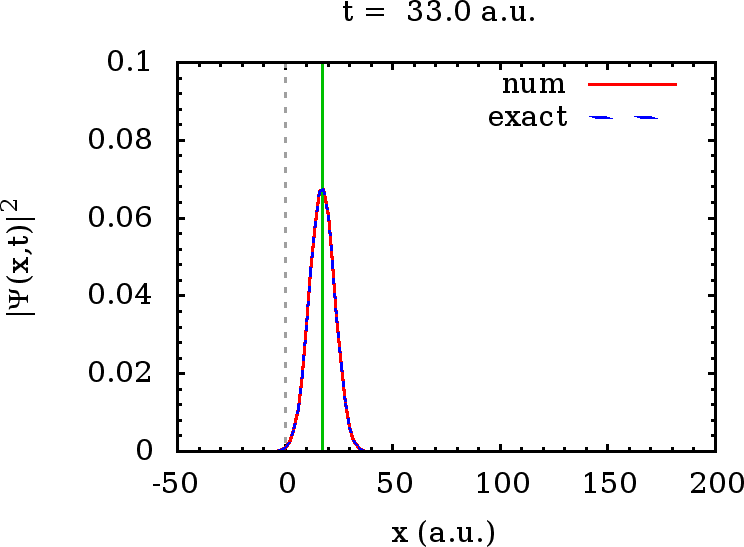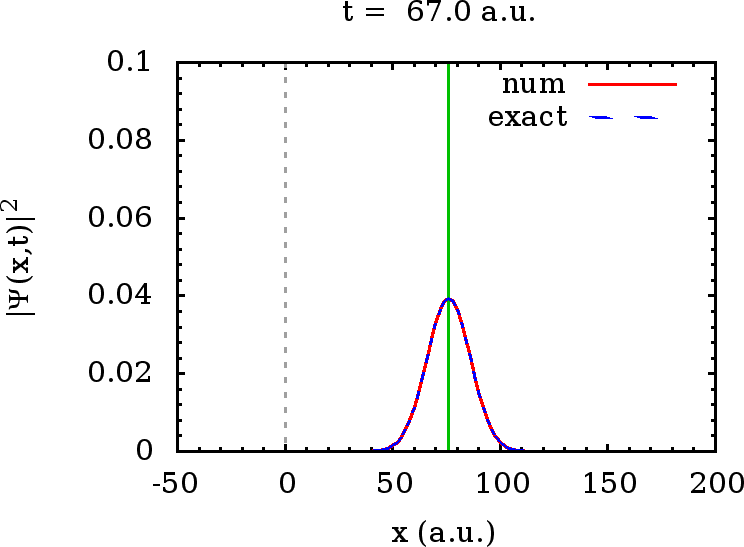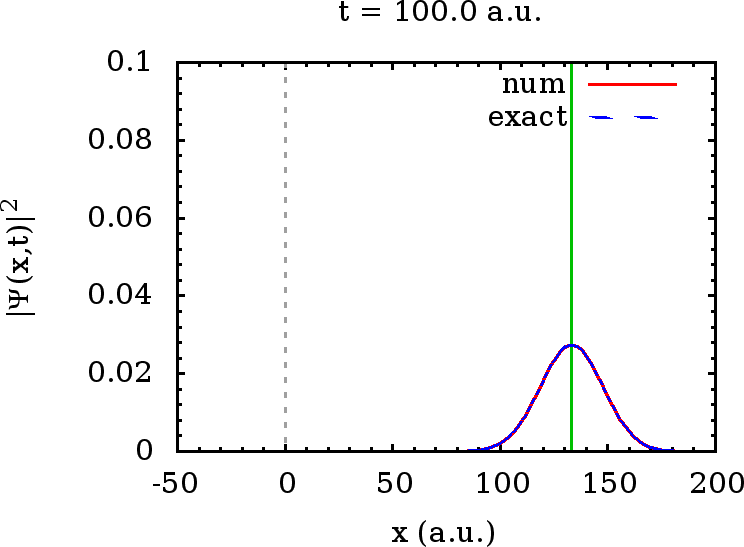
Die numerische Auswertung zeigt, daß dieses Wellenpaket (in rot gezeichnet) in der Tat mit großer Genauigkeit unser Wellenpaket (blau gestrichelt) aus Hausübung 2 reproduziert:

Wie wir in den Übungen ausführlich diskutiert haben, bleibt das Wellenpaket Gaußförmig, verbreitert sich aber aufgrund der nichtlinearen Dispersionsrelation $\omega=\hbar k^2/(2m)$ der Schrödingerwellen mit der Zeit, d.h. der ein anfänglich auf kleinem Raum genau lokalisiertes Teilchen wird mit der Zeit immer unschärfer, und zwar desto schneller, je genauer das Teilchen anfangs lokalisiert war, denn desto breiter ist das Anfangswellenpaket im Impulsraum.

Hendrik van Hees
2019-11-08