Next: Freie Teilchen Up: Allgemeines zur Lösung der Previous: Kontinuitätsgleichung
Während die Normierung der Energieeigenfunktionen für diskrete
Energieeigenwerte, also für gebundene Zustände, gemäß
(5) kein prinzipielles Problem darstellt, müssen wir die
Normierung auf die ![]() -Distribution für ungebundene Zustände
genauer ansehen. Für die Eigenfunktionen zu einfachen Eigenwerten ist
es klar, daß das Nomierungsintegral in (5)
-Distribution für ungebundene Zustände
genauer ansehen. Für die Eigenfunktionen zu einfachen Eigenwerten ist
es klar, daß das Nomierungsintegral in (5)
![]() ist, und wir müssen lediglich den Koeffizienten
bestimmen. Für die doppelt entarteten Eigenzustände ist es nicht
unmittelbar klar, daß irgendwelche zwei linear unabhängigen Lösungen
orthogonal zueinander sind, aber wir können stets Linearkombinationen
finden, die orthogonal sind.
ist, und wir müssen lediglich den Koeffizienten
bestimmen. Für die doppelt entarteten Eigenzustände ist es nicht
unmittelbar klar, daß irgendwelche zwei linear unabhängigen Lösungen
orthogonal zueinander sind, aber wir können stets Linearkombinationen
finden, die orthogonal sind.
Wir können also annehmen, daß die Eigenfunktionen einer vollständigen Basis allesamt zueinander orthogonal sind. Es bleibt uns also lediglich noch die Normierung für die ungebundenen Zustände zu bestimmen.
Beginnen wir mit dem Fall
![]() . Wir haben dann, wie eben
überlegt,
. Wir haben dann, wie eben
überlegt,
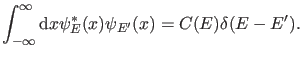 |
(33) |
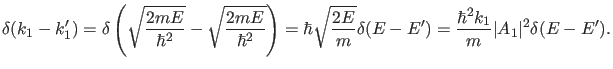 |
(35) |
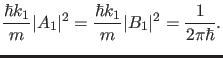 |
(36) |
Für ![]() haben wir das Problem, daß es zu jedem Energieeigenwert
zwei linear unabhängige Lösungen gibt.
haben wir das Problem, daß es zu jedem Energieeigenwert
zwei linear unabhängige Lösungen gibt.
Im folgenden wollen wir die Situation betrachten, daß ein Wellenpaket,
das zur Zeit ![]() auf einen Ort
auf einen Ort
![]() konzentriert
ist und nach rechts läuft. Dann muß zu jeder späteren Zeit der Teil
des Wellenpakets im Bereich
konzentriert
ist und nach rechts läuft. Dann muß zu jeder späteren Zeit der Teil
des Wellenpakets im Bereich
![]() ausschließlich nach
rechts laufen. D.h. wir wählen für jeden Energieeigenwert
ausschließlich nach
rechts laufen. D.h. wir wählen für jeden Energieeigenwert ![]() die
Eigenfunktion aus, für die
die
Eigenfunktion aus, für die
Die Normierung bestimmen wir ganz analog wie eben im Fall ![]() ,
wobei freilich beide asymptotischen Regionen berücksichtigt werden
müssen. Es ergibt sich die Vorschrift, daß die Wellenfunktion wieder
gemäß (37) normiert sein muß. Im Falle der
kontinuierlichen Eigenwerte bestimmt also die Norm des bei
,
wobei freilich beide asymptotischen Regionen berücksichtigt werden
müssen. Es ergibt sich die Vorschrift, daß die Wellenfunktion wieder
gemäß (37) normiert sein muß. Im Falle der
kontinuierlichen Eigenwerte bestimmt also die Norm des bei
![]() nach rechts laufenden Wellenpaketes die
Normierung.
nach rechts laufenden Wellenpaketes die
Normierung.
Die Zeitentwicklung dieser Wellenpakete ist dann gem. (6) durch
Hendrik van Hees