Betrachten wir nun also das Energieeigenwertproblem für die Potentiale
der oben beschriebenen Art. Zur Vereinfachung führen wir die folgenden
Variablen ein:
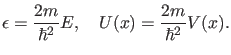 |
(9) |
Dann können wir (4) in der Form
![$\displaystyle \psi_E''(x)=[U(x)-\epsilon] \psi_E(x)$](img32.png) |
(10) |
schreiben. Wir wollen nun die Form der Wellenfunktion für
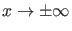 herausfinden.
herausfinden.
Für
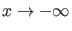 lautet die zeitunabhängige
Schrödingergleichung (10) aufgrund der Annahmen über
das asymptotische Verhalten des Potentials (2)
lautet die zeitunabhängige
Schrödingergleichung (10) aufgrund der Annahmen über
das asymptotische Verhalten des Potentials (2)
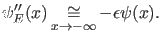 |
(11) |
Diese lineare Differentialgleichung besitzt zwei linear unabhängige
Lösungen
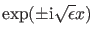 , so daß die allgemeine
Lösung eine Superposition dieser beiden Lösungen sein muß:
, so daß die allgemeine
Lösung eine Superposition dieser beiden Lösungen sein muß:
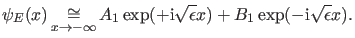 |
(12) |
Wir müssen nun noch genauer über die möglichen Energieeigenwerte
nachdenken. Falls nämlich
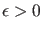 , so ist
, so ist 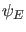 für
für
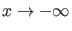 in jedem Falle ein ungebundener Zustand,
d.h.
in jedem Falle ein ungebundener Zustand,
d.h. 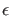 liegt im kontinuierlichen Spektrum, und es gibt keine
weiteren Einschränkungen an
liegt im kontinuierlichen Spektrum, und es gibt keine
weiteren Einschränkungen an 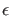 vom asymptotischen Verhalten im
Unendlichen, und dann sind allgemeine
vom asymptotischen Verhalten im
Unendlichen, und dann sind allgemeine 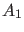 und
und 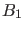 in
(12) erlaubt. Falls aber
in
(12) erlaubt. Falls aber
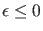 , so ist genauer
, so ist genauer
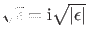 zu schreiben, und damit die
Wellenfunktion für
zu schreiben, und damit die
Wellenfunktion für
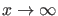 nicht exponentiell (bzw. für
nicht exponentiell (bzw. für
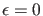 linear) anwächst, muß notwendig
linear) anwächst, muß notwendig 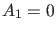 sein, d.h. wir
haben genauer
sein, d.h. wir
haben genauer
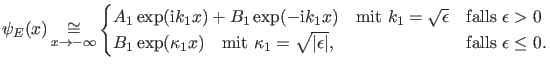 |
(13) |
Für
 ergibt sich
ergibt sich
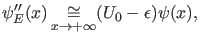 |
(14) |
und wir können exakt analoge Überlegungen wie eben anstellen. Es
ergibt sich dann schließlich
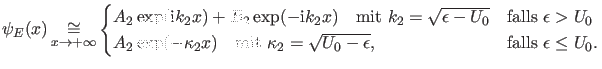 |
(15) |
Nun können wir die verschiedenen möglichen Fälle für 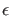 im
Hinblick auf das Verhalten der Wellenfunktionen analysieren
im
Hinblick auf das Verhalten der Wellenfunktionen analysieren
-
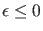 : Dies entspricht gemäß (13) und
(15) mit Sicherheit gebundenen Zuständen, d.h. die
Wellenfunktion fällt für
: Dies entspricht gemäß (13) und
(15) mit Sicherheit gebundenen Zuständen, d.h. die
Wellenfunktion fällt für
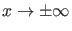 exponentiell
ab, d.h.
exponentiell
ab, d.h.
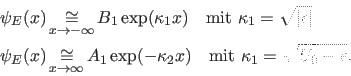 |
(16) |
Wir werden weiter unten noch zeigen, daß diesen  notwendig
diskrete Energieeigenwerte
notwendig
diskrete Energieeigenwerte
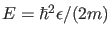 entsprechen. Daß
es sich um gebundene Zustände handeln muß, wird auch physikalisch
verständlich, wenn man sich das analoge klassische Problem vor Augen
führt: Wenn
entsprechen. Daß
es sich um gebundene Zustände handeln muß, wird auch physikalisch
verständlich, wenn man sich das analoge klassische Problem vor Augen
führt: Wenn 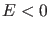 ist, kann das Teilchen weder nach
ist, kann das Teilchen weder nach
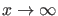 noch nach
noch nach
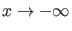 laufen, da sonst der
Energiesatz verletzt würde, denn die potentielle Energie
laufen, da sonst der
Energiesatz verletzt würde, denn die potentielle Energie
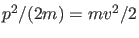 ist notwendig positiv und das Potential nach Annahme asympotisch
gleich 0 bzw.
ist notwendig positiv und das Potential nach Annahme asympotisch
gleich 0 bzw. 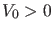 . Damit also gebundene Zustände überhaupt
möglich werden, muß das Potential irgendwo negativ werden, also eine
Art ,,Potentialmulde``bilden (vgl. Abb. 1). Unsere
eben gefundenen asymptotischen Lösungen zeigen aber, daß eine von 0
verschiedene Aufenthaltswahrscheinlichkeit des Teilchens außerhalb des
klassisch erlaubten Bereiches gibt! Dieses Phänomen ist klassisch nicht
erklärbar und wird als Tunnel- oder Gamov-Effekt
bezeichnet.
. Damit also gebundene Zustände überhaupt
möglich werden, muß das Potential irgendwo negativ werden, also eine
Art ,,Potentialmulde``bilden (vgl. Abb. 1). Unsere
eben gefundenen asymptotischen Lösungen zeigen aber, daß eine von 0
verschiedene Aufenthaltswahrscheinlichkeit des Teilchens außerhalb des
klassisch erlaubten Bereiches gibt! Dieses Phänomen ist klassisch nicht
erklärbar und wird als Tunnel- oder Gamov-Effekt
bezeichnet.
-
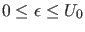 : Gemäß (13) und
(15) kann sich das Teilchen nach
: Gemäß (13) und
(15) kann sich das Teilchen nach
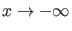 hin quasi-frei bewegen, nicht aber nach
hin quasi-frei bewegen, nicht aber nach
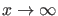 . Es
sind alle
. Es
sind alle
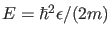 in diesem Bereich erlaubt, so daß
in diesem Bereich erlaubt, so daß
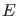 in diesem Falle zum kontinuierlichen Bereich der Energieeigenwerte
gehört. Da für
in diesem Falle zum kontinuierlichen Bereich der Energieeigenwerte
gehört. Da für
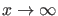 nur genau eine, nämlich die
exponentiell fallende Lösung erlaubt ist, gibt es zu jedem Wert für
nur genau eine, nämlich die
exponentiell fallende Lösung erlaubt ist, gibt es zu jedem Wert für
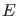 genau eine Energieeigenfunktion, d.h. dieser Teil der
Energieeigenwerte ist nicht entartet. Auch hier haben wir
wieder einen Tunneleffekt. Der Bereich
genau eine Energieeigenfunktion, d.h. dieser Teil der
Energieeigenwerte ist nicht entartet. Auch hier haben wir
wieder einen Tunneleffekt. Der Bereich
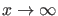 ist wie
oben erläutert für das Teilchen verboten, aber die
quantenmechanische Aufenthaltswahrscheinlichkeit ist dort nicht 0.
ist wie
oben erläutert für das Teilchen verboten, aber die
quantenmechanische Aufenthaltswahrscheinlichkeit ist dort nicht 0.
-
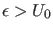 : Gemäß (13) und (15)
ist das Teilchen bzgl. der Bewegung nach beiden Richtungen
: Gemäß (13) und (15)
ist das Teilchen bzgl. der Bewegung nach beiden Richtungen
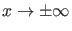 ungebunden. Die entsprechenden
Energieeigenwerte sind also alle erlaubt und gehören somit zum
kontinuierlichen Teil der Eigenwerte. In beiden Regionen sind
allgemeine Superpositionen aus zwei Lösungen erlaubt, d.h. in diesem
Bereich sind die Eigenwerte zweifach entartet. Auch das ist an dem
klassischen Analogon verständlich: Das Teilchen kann in diesem Fall
bei vorgegebener Energie in beiden asymptotischen Regionen sowohl nach
rechts (entsprechend den Wellenfunktionen mit Koeffzienten
ungebunden. Die entsprechenden
Energieeigenwerte sind also alle erlaubt und gehören somit zum
kontinuierlichen Teil der Eigenwerte. In beiden Regionen sind
allgemeine Superpositionen aus zwei Lösungen erlaubt, d.h. in diesem
Bereich sind die Eigenwerte zweifach entartet. Auch das ist an dem
klassischen Analogon verständlich: Das Teilchen kann in diesem Fall
bei vorgegebener Energie in beiden asymptotischen Regionen sowohl nach
rechts (entsprechend den Wellenfunktionen mit Koeffzienten 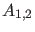 )
bzw. links (entsprechend den Wellenfunktionen mit Koeffizienten
)
bzw. links (entsprechend den Wellenfunktionen mit Koeffizienten
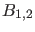 laufen.
laufen.
Abbildung:
Potential und qualitatives Energieeigenwertspektrum zum
zugehörigen Schrödingerschen Energieeigenwertproblem.
|
|
Hendrik van Hees
2019-11-08
![]() lautet die zeitunabhängige
Schrödingergleichung (10) aufgrund der Annahmen über
das asymptotische Verhalten des Potentials (2)
lautet die zeitunabhängige
Schrödingergleichung (10) aufgrund der Annahmen über
das asymptotische Verhalten des Potentials (2)
![\includegraphics[width=0.6\textwidth]{potential}](img61.png)