Kontinuitätsgleichung
Wir können weitere recht allgemeine Schlüsse aus dem asymptotischen
Verhalten der Wellenfunktionen ziehen, wenn wir die
Kontinuitätsgleichung für den hier diskutierten eindimensionalen Fall
heranziehen. Aus der zeitabhängigen Schrödingergleichung
(1) folgt sofort, daß die Gleichung
![\begin{displaymath}\begin{split}& \partial_t \varrho(x,t)+\partial_x j(x,t)=0 \q...
...ac{\hbar}{m} \im [\Psi^*(x,t) \partial_x \Psi(x,t)] \end{split}\end{displaymath}](img62.png) |
(17) |
gilt. Für eine quadratintegrable Funktion 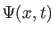 bedeutet dies,
daß die Normierung der Wellenfunktion mit der Zeit konstant bleibt
(s. Vorlesung), d.h. hat man
bedeutet dies,
daß die Normierung der Wellenfunktion mit der Zeit konstant bleibt
(s. Vorlesung), d.h. hat man 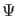 zur Zeit
zur Zeit 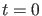 auf
auf 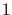 normiert, so
ist dies automatisch auch für alle späteren Zeiten gewährleistet,
vorausgesetzt
normiert, so
ist dies automatisch auch für alle späteren Zeiten gewährleistet,
vorausgesetzt 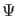 erfüllt die Schrödingergleichung. Mathematisch
gesehen ist dies Folge der Unitarität des
Zeitentwicklungsoperators, die aus der Hermitezität des
Hamiltonoperators folgt.
erfüllt die Schrödingergleichung. Mathematisch
gesehen ist dies Folge der Unitarität des
Zeitentwicklungsoperators, die aus der Hermitezität des
Hamiltonoperators folgt.
Für die Energieeigenfunktionen
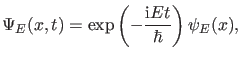 |
(18) |
wobei hier 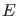 sowohl im diskreten als auch im kontinuierlichen Teil des
Spektrums liegen darf, ist offenbar die Wahrscheinlichkeitsdichte
sowohl im diskreten als auch im kontinuierlichen Teil des
Spektrums liegen darf, ist offenbar die Wahrscheinlichkeitsdichte
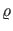 zeitlich konstant. Dies zeichnet die Energieeigenfunktionen
physikalisch als die stationären Zustände des Systems aus:
Die Wahrscheinlichkeitsverteilung als die in der Wellenfunktion
enthaltene physikalisch relevante Information ist zeitlich
konstant. Demgemäß muß aufgrund der Kontinuitätsgleichung auch der
Strom zeitlich konstant sein. In der Tat folgt für die Wellenfunktion
(18)
zeitlich konstant. Dies zeichnet die Energieeigenfunktionen
physikalisch als die stationären Zustände des Systems aus:
Die Wahrscheinlichkeitsverteilung als die in der Wellenfunktion
enthaltene physikalisch relevante Information ist zeitlich
konstant. Demgemäß muß aufgrund der Kontinuitätsgleichung auch der
Strom zeitlich konstant sein. In der Tat folgt für die Wellenfunktion
(18)
![$\displaystyle j_E(x,t)=j_E(x)=\frac{\hbar}{m} \im [\psi_E^*(x) \psi_E'(x) ].$](img67.png) |
(19) |
Aus der Kontinuitätsgleichung folgt weiter
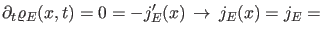 const const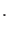 |
(20) |
Der Strom ist also eine Konstante.
Wir können nun den Strom für die Energieeigenzustände aus dem oben
hergeleiteten asymptotischen Verhalten bestimmen.
Für gebundene Zustände (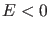 ) und die Zustände zu den einfach
entarteten Energieeigenwerten im Kontinuierlichen Spektrum
) und die Zustände zu den einfach
entarteten Energieeigenwerten im Kontinuierlichen Spektrum
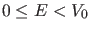 , ergibt sich für
, ergibt sich für
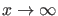 , daß
, daß 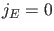 sein
muß.
sein
muß.
Für
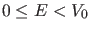 gilt andererseits im Limes
gilt andererseits im Limes
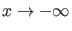
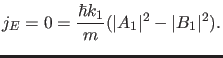 |
(21) |
Es muß also
 sein. Durch geeignete Wahl
der Phasenfaktoren der entsprechenden beiden nach rechts bzw. links
laufenden Teilwellen, können wir demnach stets erreichen, daß mit
sein. Durch geeignete Wahl
der Phasenfaktoren der entsprechenden beiden nach rechts bzw. links
laufenden Teilwellen, können wir demnach stets erreichen, daß mit
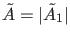 gilt
gilt
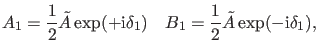 |
(22) |
und dies in (15) eingesetzt ergibt
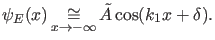 |
(23) |
Für 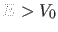 ergibt die Stromerhaltung für die Koeffizienten der
asymptotischen Wellenfunktion
ergibt die Stromerhaltung für die Koeffizienten der
asymptotischen Wellenfunktion
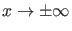
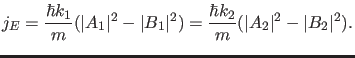 |
(24) |
Wir wenden uns nun nochmals den möglicherweise existierenden gebundenen
Zuständen zu. Vernachlässigen wir einen Moment die Bedingung der
Quadratintegrabialität der Wellenfunktionen, gibt es i.a. zu jedem
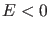 zwei linear unabhängige Lösungen, die sich jeweils so wählen
lassen, daß die eine im positiv Unendlichen, die andere im negativ
Unendlichen exponentiell fällt:
zwei linear unabhängige Lösungen, die sich jeweils so wählen
lassen, daß die eine im positiv Unendlichen, die andere im negativ
Unendlichen exponentiell fällt:
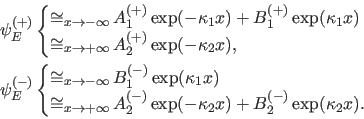 |
(25) |
Es kann also nur dann ein gebundener Zustand vorliegen, wenn
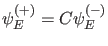 mit
mit
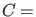 const. Dies zeigt, wie
schon oben erläutert, daß die zu gebundenen Zuständen gehörigen
Energieeigenwerte
const. Dies zeigt, wie
schon oben erläutert, daß die zu gebundenen Zuständen gehörigen
Energieeigenwerte 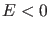 nicht entartet sind, d.h. wenn ein gebundener
Zustand existiert, ist die dazugehörige Eigensfunktion bis auf eine
Normierungsonstante eindeutig bestimmt.
nicht entartet sind, d.h. wenn ein gebundener
Zustand existiert, ist die dazugehörige Eigensfunktion bis auf eine
Normierungsonstante eindeutig bestimmt.
Wir betrachten nun die Wronskideterminante zu zwei Lösungen von
(10) zu Energieeigenwerten 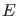 und
und 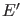
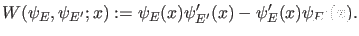 |
(26) |
Aus (10) folgt dann unmittelbar
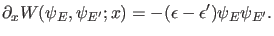 |
(27) |
Für irgendein festes 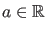 ist also
ist also
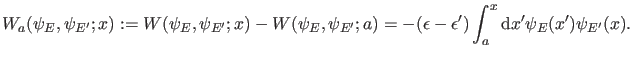 |
(28) |
Es seien weiter zu jedem Wert 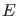 die Funktionen
die Funktionen
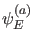 die
Lösungen der Schrödingergleichung mit fixierten Anfangsbedingungen bei
die
Lösungen der Schrödingergleichung mit fixierten Anfangsbedingungen bei
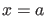 :
:
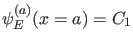 ,
,
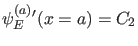 . Für
diese Funktionen gilt dann offenbar
. Für
diese Funktionen gilt dann offenbar 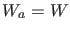 .
.
Jetzt betrachten wir die Ableitung von 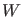 für diese Funktionen nach
für diese Funktionen nach
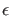 in der Umgebung eines Eigenwertes im kontinuierlichen
Spektrum. Bezeichne dazu
in der Umgebung eines Eigenwertes im kontinuierlichen
Spektrum. Bezeichne dazu 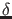 die Variation der jeweiligen Größe
bei einer Änderung von
die Variation der jeweiligen Größe
bei einer Änderung von 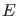 zu
zu
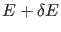 bzw.
bzw. 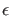 zu
zu
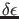 . Dann folgt einerseits aus (28)
. Dann folgt einerseits aus (28)
![$\displaystyle \delta W_a=W(\psi_E^{(a)},\psi_E^{(a)}+\delta \psi_{E}^{(a)};x) =...
...elta \psi_{E}^{(a)};x)=-\delta \epsilon \int_{a}^{x} \dd x [\psi_E^{(a)}(x)]^2.$](img95.png) |
(29) |
Andererseits folgt für
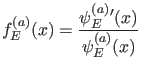 |
(30) |
bei Variation nach 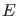 :
:
![$\displaystyle \delta f_E^{(a)}(x) = \frac{W(\psi_E^{(a)},\delta \psi_E^{(a)};x)}{[\psi_E^{(a)}]^2}$](img97.png) |
(31) |
Kombiniert man dies mit (29), erhält man
![$\displaystyle \partial_{\epsilon} f_E^{(a)}(x)=-\frac{1}{[\psi_E^{(a)}(x)]^2} \int_{a}^{x} \dd x [\psi_E^{(a)}(x)]^2.$](img98.png) |
(32) |
Das bedeutet, daß die logarithmische Ableitung der
Energieeigenfunktionen zu fixierten Anfangsbedingungen bei 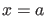 monoton
fallend für
monoton
fallend für 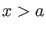 und monoton wachsend für
und monoton wachsend für 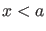 als Funktionen von
als Funktionen von
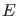 (bzw.
(bzw. 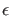 ) sind.
) sind.
Nehmen wir nun an, es sei 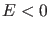 ein Eigenwert im kontinuierlichen Teil
des Eigenwertspektrums. Wir können dann für die Wellenfunktionen
ein Eigenwert im kontinuierlichen Teil
des Eigenwertspektrums. Wir können dann für die Wellenfunktionen
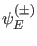 offenbar
offenbar
 wählen. Die
Funktion
wählen. Die
Funktion
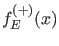 ist also bei festgehaltenem
ist also bei festgehaltenem 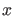 als Funktionen
von
als Funktionen
von 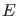 stets monoton wachsend und
stets monoton wachsend und
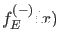 monoton fallend. Wie
wir oben gezeigt haben, müssen die Wellenfunktionen
monoton fallend. Wie
wir oben gezeigt haben, müssen die Wellenfunktionen
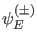 aber (bis auf eine multiplikative Konstante) gleich sein, und das
bedeutet
aber (bis auf eine multiplikative Konstante) gleich sein, und das
bedeutet
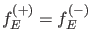 . Dies ist ein Widerspruch, und daher muß
jedes
. Dies ist ein Widerspruch, und daher muß
jedes 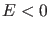 notwendig zum diskreten Spektrum gehören.
notwendig zum diskreten Spektrum gehören.
Hendrik van Hees
2019-11-08
![]() ) und die Zustände zu den einfach
entarteten Energieeigenwerten im Kontinuierlichen Spektrum
) und die Zustände zu den einfach
entarteten Energieeigenwerten im Kontinuierlichen Spektrum
![]() , ergibt sich für
, ergibt sich für
![]() , daß
, daß ![]() sein
muß.
sein
muß.
![]() gilt andererseits im Limes
gilt andererseits im Limes
![]()
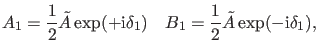
![]() zwei linear unabhängige Lösungen, die sich jeweils so wählen
lassen, daß die eine im positiv Unendlichen, die andere im negativ
Unendlichen exponentiell fällt:
zwei linear unabhängige Lösungen, die sich jeweils so wählen
lassen, daß die eine im positiv Unendlichen, die andere im negativ
Unendlichen exponentiell fällt:
![]() und
und ![]()
![]() für diese Funktionen nach
für diese Funktionen nach
![]() in der Umgebung eines Eigenwertes im kontinuierlichen
Spektrum. Bezeichne dazu
in der Umgebung eines Eigenwertes im kontinuierlichen
Spektrum. Bezeichne dazu ![]() die Variation der jeweiligen Größe
bei einer Änderung von
die Variation der jeweiligen Größe
bei einer Änderung von ![]() zu
zu
![]() bzw.
bzw. ![]() zu
zu
![]() . Dann folgt einerseits aus (28)
. Dann folgt einerseits aus (28)
![]() ein Eigenwert im kontinuierlichen Teil
des Eigenwertspektrums. Wir können dann für die Wellenfunktionen
ein Eigenwert im kontinuierlichen Teil
des Eigenwertspektrums. Wir können dann für die Wellenfunktionen
![]() offenbar
offenbar
![]() wählen. Die
Funktion
wählen. Die
Funktion
![]() ist also bei festgehaltenem
ist also bei festgehaltenem ![]() als Funktionen
von
als Funktionen
von ![]() stets monoton wachsend und
stets monoton wachsend und
![]() monoton fallend. Wie
wir oben gezeigt haben, müssen die Wellenfunktionen
monoton fallend. Wie
wir oben gezeigt haben, müssen die Wellenfunktionen
![]() aber (bis auf eine multiplikative Konstante) gleich sein, und das
bedeutet
aber (bis auf eine multiplikative Konstante) gleich sein, und das
bedeutet
![]() . Dies ist ein Widerspruch, und daher muß
jedes
. Dies ist ein Widerspruch, und daher muß
jedes ![]() notwendig zum diskreten Spektrum gehören.
notwendig zum diskreten Spektrum gehören.