Im folgenden betrachten wir Lösungen der zeitabhängigen
Schrödingergleichung für die eindimensionale Bewegung eines Teilchens
in einem Potential entlang der 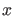 -Achse:
-Achse:
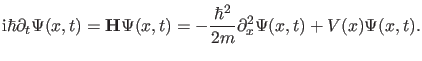 |
(1) |
Wir werden uns auf die grundlegenden physikalischen Argumente
beschränken. Eine ausführlichere Behandlung der mathematischen
Struktur der Schrödingergleichung findet sich in [Mes99].
Wir betrachten Potentiale, die im Unendlichen bestimmten konstanten
Grenzwerten zustreben:
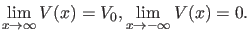 |
(2) |
Dabei muß die Konvergenz gegen diese Werte schneller als mit 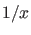 erfolgen, d.h. es soll genauer
erfolgen, d.h. es soll genauer
![$\displaystyle \lim_{x \rightarrow \infty} x[V(x)-V_0]=0, \quad \lim_{x \rightarrow -\infty} x V(x)=0$](img14.png) |
(3) |
gelten. Es ist klar, daß die Wahl 0 des Grenzwertes für
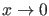 keine Beschränkung der Allgemeinheit bedeutet, da wir in
dem Falle, daß das Potential dort gegen einen anderen Grenzwert strebt,
durch eine einfache Verschiebung des Energienullpunkts die hier
betrachtete Situation herstellen können, ohne daß dies den
physikalischen Gehalt der Betrachtung ändert.
keine Beschränkung der Allgemeinheit bedeutet, da wir in
dem Falle, daß das Potential dort gegen einen anderen Grenzwert strebt,
durch eine einfache Verschiebung des Energienullpunkts die hier
betrachtete Situation herstellen können, ohne daß dies den
physikalischen Gehalt der Betrachtung ändert.
Wir können nun die allgemeine Lösung der zeitabhängigen
Schrödingergleichung (1) nach Energieeigenfunktionen
entwickeln. Die Energieeigenfunktionen sind durch das Eigenwertproblem
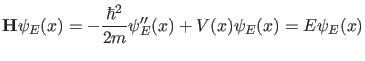 |
(4) |
gegeben. Dabei wird i.a. die Menge der Energieeigenwerte sowohl einen
diskreten als auch einen kontinuierlichen Anteil enthalten. Wie wir
gleich sehen werden, entsprechen die diskreten Energieeigenwerte
gebundenen Zuständen, denn die dazugehörigen Energieeigenfunktionen
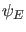 sind quadratintegrabel und können auf
sind quadratintegrabel und können auf 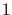 normiert werden. Die
Eigenfunktionen zu kontinuierlichen Eigenwerten besitzen im Unendlichen
asymptotisch den Charakter ebener Wellen und beschreiben dort somit die
ungebundene ,,quasifreie``Bewegung des Teilchens. Diese
Wellenfunktionen werden auf die
normiert werden. Die
Eigenfunktionen zu kontinuierlichen Eigenwerten besitzen im Unendlichen
asymptotisch den Charakter ebener Wellen und beschreiben dort somit die
ungebundene ,,quasifreie``Bewegung des Teilchens. Diese
Wellenfunktionen werden auf die 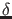 -Distribution in der Energie
normiert.
-Distribution in der Energie
normiert.
Numerieren wir die diskreten Energieeigenwerte und -eigenfunktionen mit
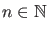 durch (dabei können je nach der konkreten Form des
Potentials i.a. sowohl endlich oder unendlich viele als auch gar keine
diskreten Energieeigenwerte existieren) und bezeichnen die Menge der
kontinuierlichen Eigenwerte mit
durch (dabei können je nach der konkreten Form des
Potentials i.a. sowohl endlich oder unendlich viele als auch gar keine
diskreten Energieeigenwerte existieren) und bezeichnen die Menge der
kontinuierlichen Eigenwerte mit
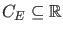 , so verlangen wir
also
, so verlangen wir
also
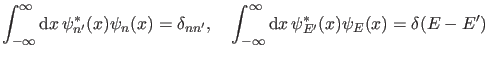 für für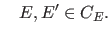 |
(5) |
Daß die Eigenfunktionen zu verschiedenen Energieeigenwerten orthogonal
zueinander sind, folgt allgemein aus der Hermitezität des
Hamiltonoperators (s. Vorlesung).
Es ist dann leicht zu zeigen, daß in der Tat jede Funktion
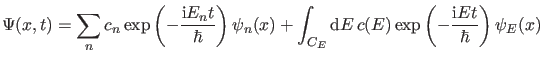 |
(6) |
die zeitabhängige Schrödingergleichung (1) löst.
Wie man leicht mit Hilfe der Orthonormierungsbedingungen
(5) nachweist (vgl. Präsenzübung 6 c), hängt die
Normierung von 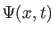 mit der Normierung der
mit der Normierung der 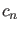 und
und
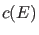 zusammen vermöge
zusammen vermöge
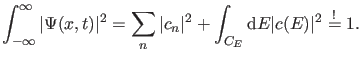 |
(7) |
Bei vorgegebener Anfangswellenfunktion
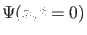 sind die
Koeffizienten
sind die
Koeffizienten 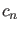 und
und 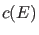 in (6) durch
in (6) durch
 |
(8) |
bestimmt (man rechne das nach!). Haben wir uns die Energieeigenwerte und
Energieeigenfunktionen beschafft, können wir also die
Schrödingergleichung bei irgendeiner vorgegebenen Anfangsbedingung
lösen, wobei i.a. die Entwicklung (6) i.a. nur numerisch
konkret ausgewertet werden kann.
Hendrik van Hees
2019-11-08
![]() -Achse:
-Achse:
![]() durch (dabei können je nach der konkreten Form des
Potentials i.a. sowohl endlich oder unendlich viele als auch gar keine
diskreten Energieeigenwerte existieren) und bezeichnen die Menge der
kontinuierlichen Eigenwerte mit
durch (dabei können je nach der konkreten Form des
Potentials i.a. sowohl endlich oder unendlich viele als auch gar keine
diskreten Energieeigenwerte existieren) und bezeichnen die Menge der
kontinuierlichen Eigenwerte mit
![]() , so verlangen wir
also
, so verlangen wir
also
![]() mit der Normierung der
mit der Normierung der ![]() und
und
![]() zusammen vermöge
zusammen vermöge