Streuzustände

In der Streutheorie betrachtet man i.a. die Frage, mit welcher Wahrscheinlichkeit ein Teilchen in eine gegebene Richtung gestreut wird. Diese Information wird im sog. Streuquerschnitt angegeben. Darauf wollen wir in diesem Artikel nicht näher eingehen.

In unserem eindimensionalen Fall entsprechen diesen Wahrscheinlichkeiten die Transmissions- und Emissionskoeffizienten, die das Verhältnis der Größe des reflektierten bzw. durch die Schwelle hindurchgehenden Stromes von Teilchen angeben. Die Zustände, die wir dabei betrachtet haben, sind die stationären Energieeigenzustände. Praktisch meßbar ist so ein Strom, indem man sehr viele voneinander unabhängige Experimente mit jeweils einem Teilchen durchführt und dann die Wahrscheinlichkeitsströme als relative Häufigkeiten mißt. Dabei schickt man ein Teilchen mit recht genau bestimmter Energie, weit weg von der Potentialschwelle los und zählt nach sehr langer Zeit, wieviele Teilchen weit weg von der Schwelle reflektiert bzw. wieviele durch die Schwelle hindurchgelangt sind.

Wellenmechanisch wird diese Situation durch einen halbseitig unendlichen Wellenzug bestimmter Frequenz beschrieben, dessen Kopf sich zur Zeit $t=0$ weit weg von der Potentialschwelle befindet und auf die Schwelle zuläuft. Dies bezeichnet man in der Streutheorie als einen asymptotisch freien einlaufenden Zustand bzw. kurz als ,,in-Zustand``. Danach betrachtet man die Situation wieder sehr lange nachdem der Wellenkopf auf die Potentialschwelle getroffen ist. Für asymptotisch große Zeiten hat man dann den stationären Endzustand (out-Zustand) erreicht.

Auch diese Situation läßt sich numerisch simulieren. Wir müssen uns nur passenden in-Zustand (d.h. die Wellenfunktion zur Zeit $t=0$) verschaffen. Im Impulsraum ist dieser Zustand durch

$$\phi_0(k)=\frac{\ii}{\sqrt{2 \pi}} \frac{\exp(-\ii k x_0)}{k-k_0+\ii 0^+}$$ (53)

gegeben. In der Ortsdarstellung erhalten wir

$$\phi_0(x)=\int_{-\infty}^{\infty} \frac{\dd k}{2 \pi} \phi_0(k) \exp(\ii k x).$$ (54)

Setzen wir für $\phi_0(k)$ (53) ein, sehen wir, daß wir das Integral über den Residuensatz berechnen können, indem wir den Integrationsweg in der oberen bzw. unteren Halbebene durch einen beliebig großen Halbkreis schließen. Damit dieser Halbkreis keinen divergenten Beitrag zum Integral liefert müssen wir wegen der Exponentialfunktion für $x>x_0$ den oberen und für $x<x_0$ den unteren Halbkreis wählen. Da nur in der unteren Halbebene bei $k=k_0-\ii 0^+$ ein Pol liegt, haben wir nach dem Residuensatz

$$\phi_0(x)=\frac{\Theta(x_0-x)}{\sqrt{2 \pi}} \exp[\ii k_0 (x-x_0)].$$ (55)

Diese Wellenfunktion besitzt für $x_0 \rightarrow \infty$ die korrekte Normierung einer ebenen Welle auf die $\delta$-Funktion bzgl. $k$. Es handelt sich jedenfalls um einen Wellenzug, der für $x<x_0$ einer ebenen Welle für ein nach rechts laufendes Teilchen mit Impuls $k_0$.

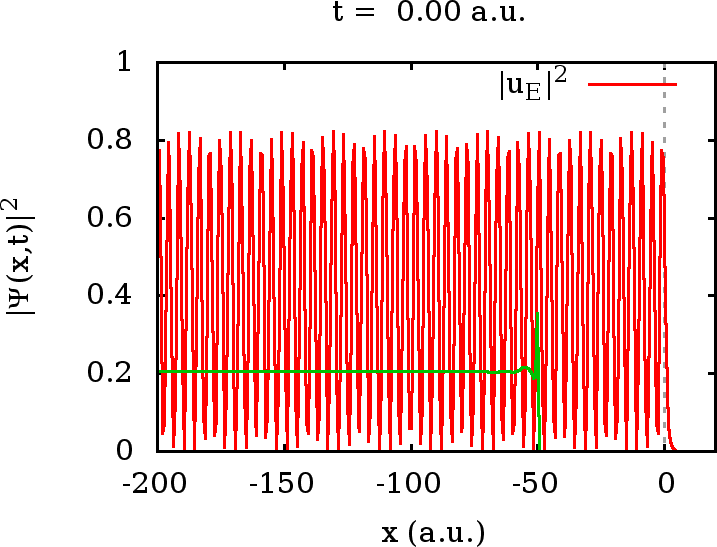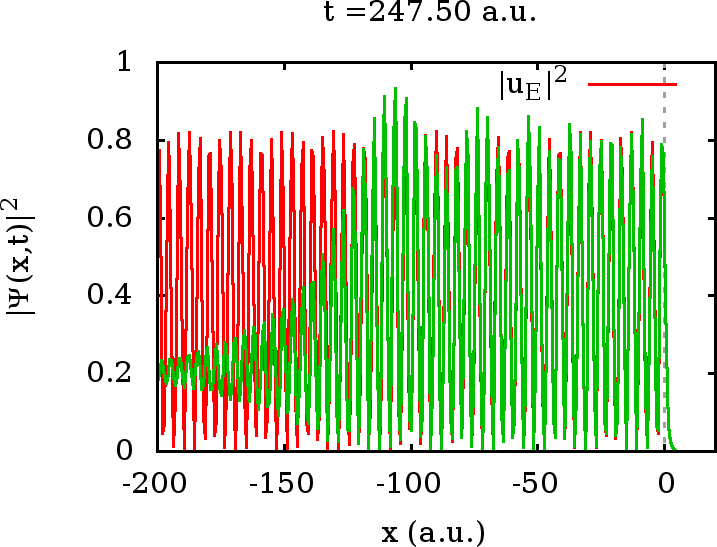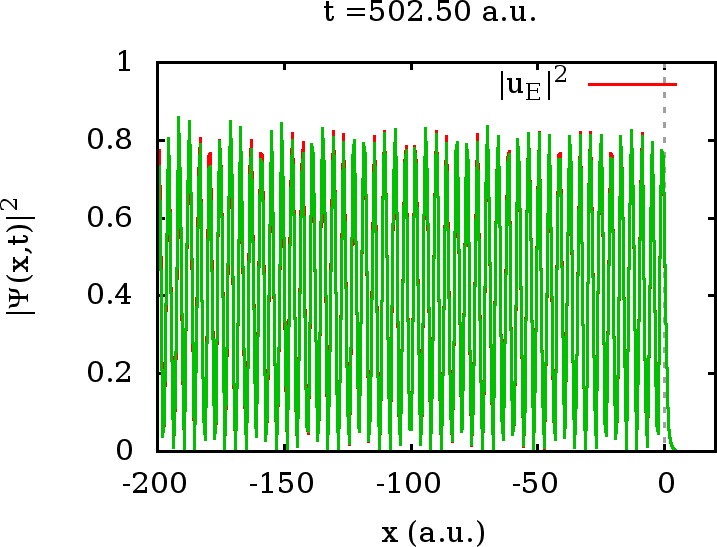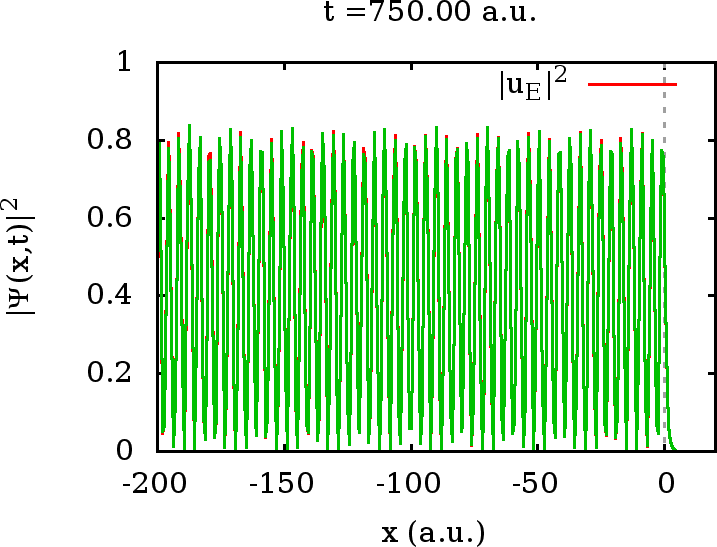
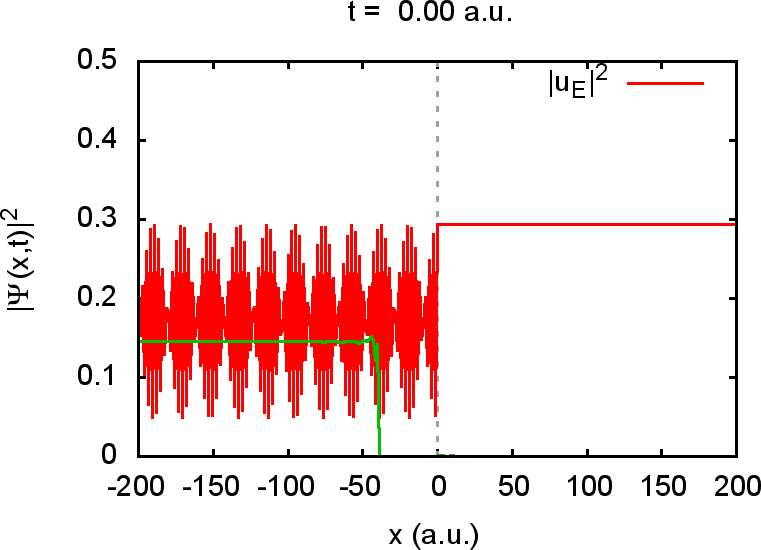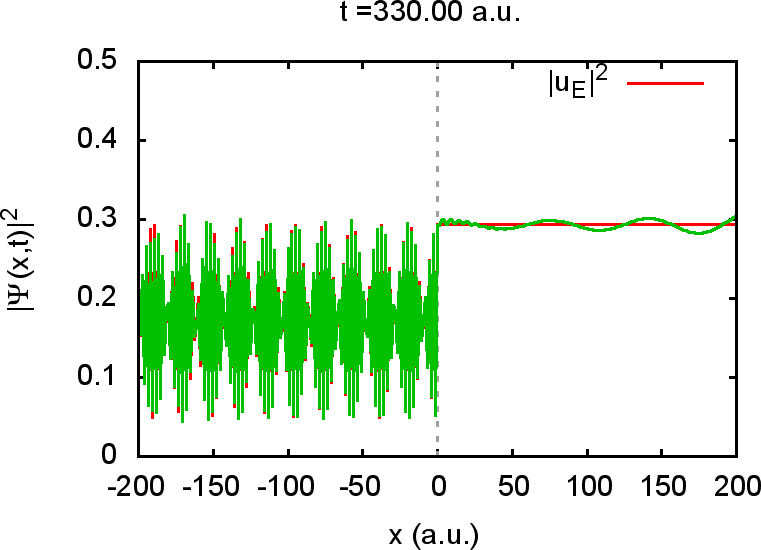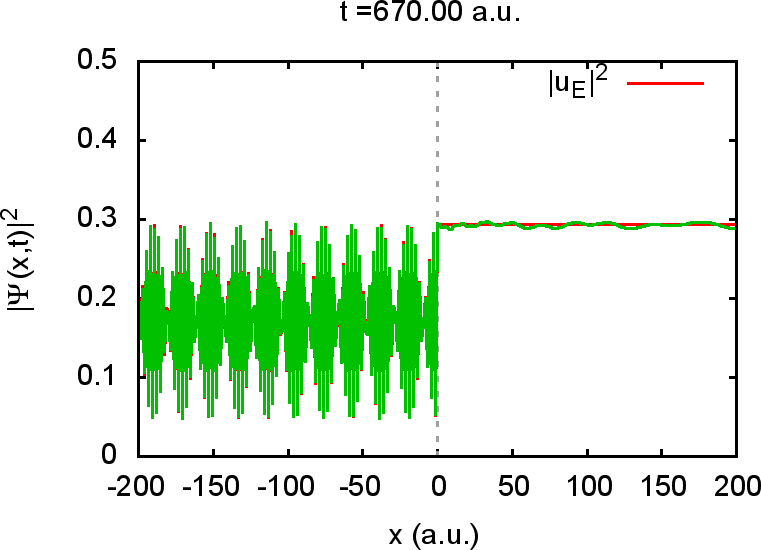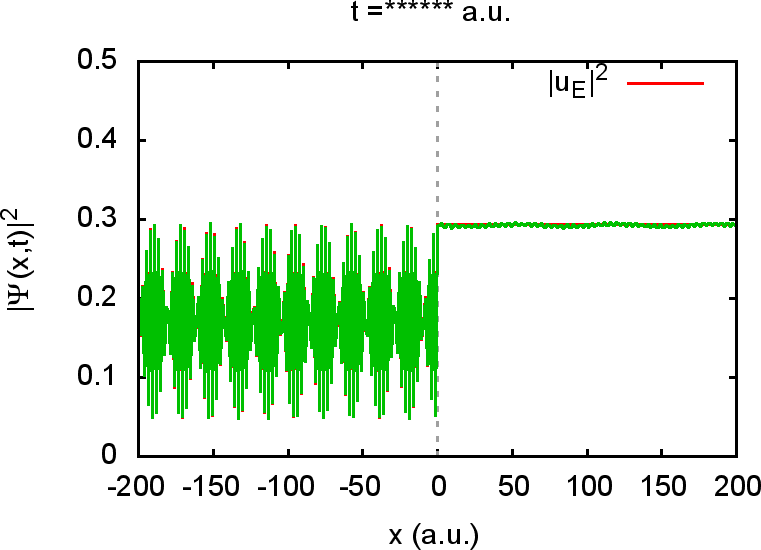
Die Wellenfunktion für beliebige Zeiten erhalten wir wieder, indem wir wie oben erläutert, mittels Energieeigenfunktionen die Zeitentwicklung berechnen. Die numerische Auswertung wird in den folgenden beiden Movies gezeigt.

Im ersten Movie ist $E_0=\hbar^2 k_0^2/(2m)=0.6 V_0$ gesetzt. In diesem Fall haben wir Totalreflexion, und die Welle dringt nur mit einem exponentiell fallenden Anteil in den Bereich $x>0$ vor. Für $x \rightarrow \infty$ ist also der nach rechts gerichtete Strom 0, wie aufgrund des Transmissionskoeffizienten in (49) zu erwarten. Für große Zeiten wird der Wellenzug (in grün eingezeichnet) in dem gezeigten $x$-Ausschnitt stationär und identisch mit der rot eingezeichneten Energieeigenfunktion zu der gegebenen Energie $E_0$:

Im zweiten Beispiel ist $E=1.2 V_0$ gesetzt, d.h. wir haben gemäß (49) sowohl einen reflektierten als auch einen durchlaufenden Anteil. Für große Zeiten nähert sich der als asymptisch freier Anfangszustand gestartete Wellenzug (grün) wieder der stationären Lösung (rot) beliebig genau an: