Next: Kleiner durchlaufender Anteil () Up: Potentialschwelle Previous: Potentialschwelle
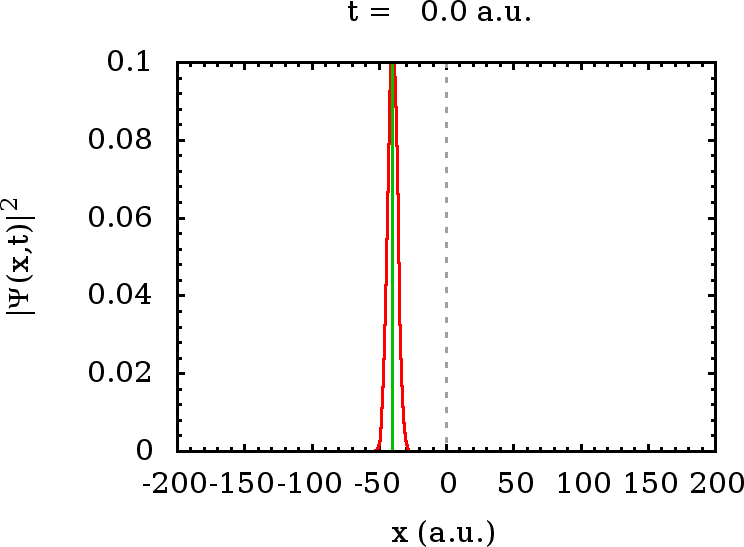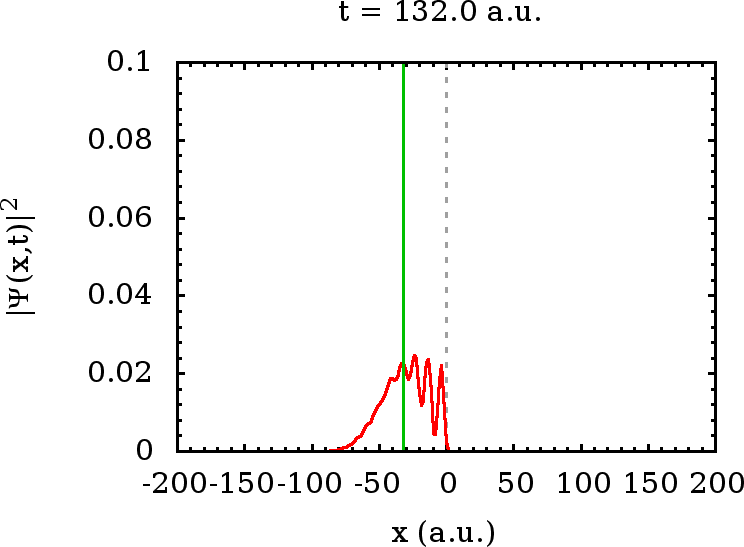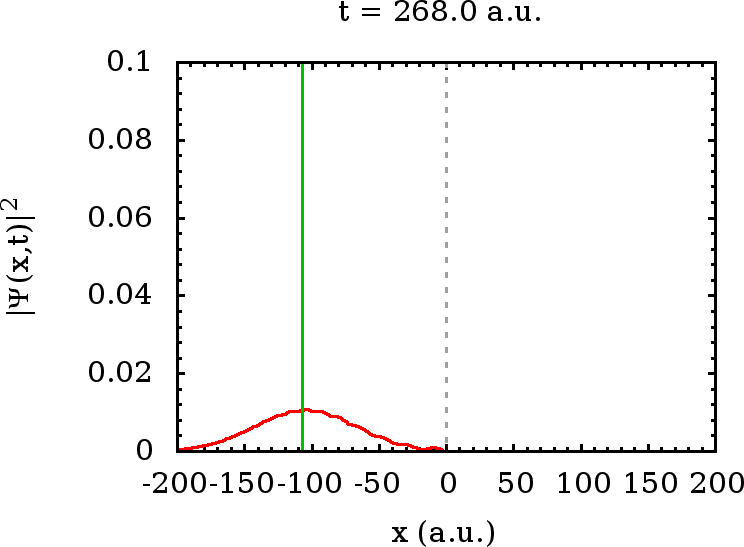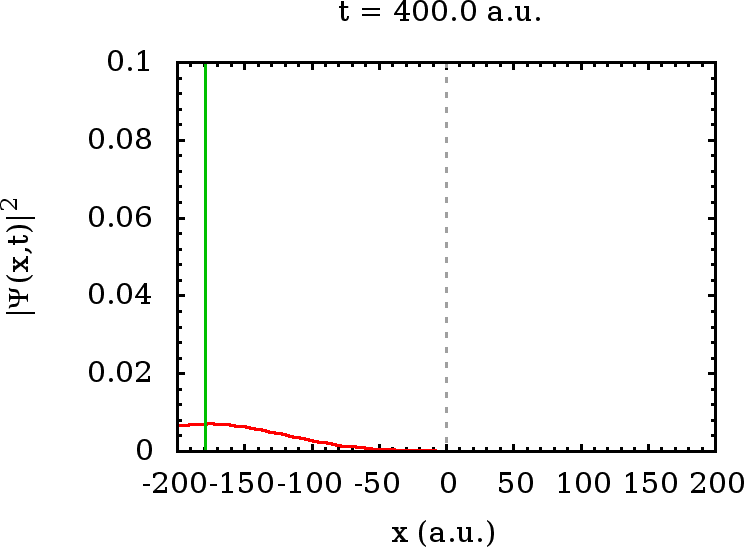
Eine weitere interessante Eigenschaft ergibt sich noch aus dem Vergleich
des Wellenpakets zum Verhalten eines klassischen Teilchens, das mit der
mittleren Energie ![]() auf die Schwelle zuläuft. In der klassischen
Mechanik wird das Teilchen in der hier simulierten Situation einfach
instantan reflektiert. Die Position dieses klassischen Teilchens wird im
Movie durch die vertikal eingezeichnete grüne Linie dargestellt. Wir
sehen, daß sich zu Zeiten nicht zu lange, nachdem die ersten Teile der
Wellenfront auf die Schwelle getroffen sind, der Schwerpunkt des
reflektierten Anteils des Wellenpaketes gegenüber dem reflektierten
klassischen Teilchen verzögert bewegt. Auch dies ist ein spezifisch
quantenmechanischer Effekt, der durch die Phasenverschiebung der
Teilwellen bei der Reflexion entsteht. Diese Phasenverschiebung läßt
sich übrigens analysieren, indem man die Koeffizienten der
Energieeigenmoden (46) analysiert.
auf die Schwelle zuläuft. In der klassischen
Mechanik wird das Teilchen in der hier simulierten Situation einfach
instantan reflektiert. Die Position dieses klassischen Teilchens wird im
Movie durch die vertikal eingezeichnete grüne Linie dargestellt. Wir
sehen, daß sich zu Zeiten nicht zu lange, nachdem die ersten Teile der
Wellenfront auf die Schwelle getroffen sind, der Schwerpunkt des
reflektierten Anteils des Wellenpaketes gegenüber dem reflektierten
klassischen Teilchen verzögert bewegt. Auch dies ist ein spezifisch
quantenmechanischer Effekt, der durch die Phasenverschiebung der
Teilwellen bei der Reflexion entsteht. Diese Phasenverschiebung läßt
sich übrigens analysieren, indem man die Koeffizienten der
Energieeigenmoden (46) analysiert.
Hendrik van Hees