Aufgaben - Kapitel 3
- Diskutieren Sie die allgemeine Lösung
des harmonischen Oszillators
- a)
- Zu welcher Zeit
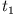 erreicht der Oszillator seinen Maximalausschlag
erreicht der Oszillator seinen Maximalausschlag 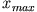 ? Wie groß ist
? Wie groß ist 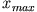 ? Welchen
Wert hat die Beschleunigung zur Zeit
? Welchen
Wert hat die Beschleunigung zur Zeit 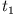 ?
?
Hinweis :
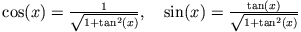
- b)
- Zu welcher Zeit
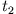 erreicht der Oszillator seine Maximalgeschwindigkeit
erreicht der Oszillator seine Maximalgeschwindigkeit
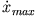 ? Wie groß ist
? Wie groß ist
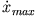 ? Wie groß ist die Auslenkung zur Zeit
? Wie groß ist die Auslenkung zur Zeit 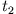 ? Welche einfache Beziehung besteht zwischen
? Welche einfache Beziehung besteht zwischen 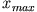 und
und
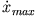 ?
?
- c)
- Zu welcher Zeit
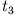 erfährt der Oszillator die maximale Beschleunigung
erfährt der Oszillator die maximale Beschleunigung
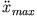 ? Wie groß ist
diese? Welche Werte haben Auslenkung und Geschwindigkeit zur Zeit
? Wie groß ist
diese? Welche Werte haben Auslenkung und Geschwindigkeit zur Zeit 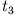 ?
?

- Machen Sie sich die Analogie zwischen einem gedämpften harmonischen Oszillator mit äußerer Kraft und einem
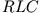 -Kreis
(Widerstand R, Induktivität L, Kapazität C) mit elektromotorischer Kraft (EMK) klar. Schreiben
Sie sich dazu sowohl die Differentialgleichung des mechanischen Oszillators als auch die Ladungsdifferentialgleichung,
Spannungsdifferentialgleichung und Stromdifferentialgleichung des
-Kreis
(Widerstand R, Induktivität L, Kapazität C) mit elektromotorischer Kraft (EMK) klar. Schreiben
Sie sich dazu sowohl die Differentialgleichung des mechanischen Oszillators als auch die Ladungsdifferentialgleichung,
Spannungsdifferentialgleichung und Stromdifferentialgleichung des 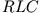 -Kreises auf. Benutzen Sie zur 'Herleitung' der
Stromdifferentialgleichung den Kirchhoffschen Spannungssatz
-Kreises auf. Benutzen Sie zur 'Herleitung' der
Stromdifferentialgleichung den Kirchhoffschen Spannungssatz
Die Ladungsdifferentialgleichung erhalten Sie aus dem Kirchhoffschen Spannungssatz mit Hilfe der Beziehung
Aus der Ladungsdifferentialgleichung gewinnen Sie mit
die Spannungsdifferentialgleichung.
Lösen Sie die Stromdifferentialgleichung für den Fall schwacher Dämpfung
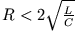 und einer
konstanten EMK (homogene Differentialgleichung!) Es gelte
und einer
konstanten EMK (homogene Differentialgleichung!) Es gelte 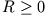 sowie
sowie 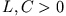 .
.

- Betrachten Sie einen ungestörten und ungedämpften harmonischen Oszillator: eine Masse m, die an einer Feder
mit der Steifigkeit
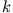 befestigt ist. Zur Zeit
befestigt ist. Zur Zeit 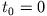 wird der in ihrer Gleichgewichtslage ruhenden Masse eine
Anfangsgeschwindigkeit
wird der in ihrer Gleichgewichtslage ruhenden Masse eine
Anfangsgeschwindigkeit 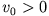 erteilt, so dass der Oszillator zu schwingen beginnt. Stellen Sie die Differentialgleichung
auf und lösen Sie diese. In welchem Verhältnis muss m zu k stehen, damit die Masse sich 1 Sekunde nach Beginn der Bewegung
wieder in der Gleichgewichtslage befindet? Wie lautet in diesem Fall das Bewegungsgesetz des Oszillators?
erteilt, so dass der Oszillator zu schwingen beginnt. Stellen Sie die Differentialgleichung
auf und lösen Sie diese. In welchem Verhältnis muss m zu k stehen, damit die Masse sich 1 Sekunde nach Beginn der Bewegung
wieder in der Gleichgewichtslage befindet? Wie lautet in diesem Fall das Bewegungsgesetz des Oszillators?

- Diskutieren Sie die allgemeine Lösung des harmonischen Oszillators aus der Sicht des Energieerhaltungssatzes.
- a)
- Warum gilt dieser?
- b)
- Benutzen Sie den Energieerhaltungssatz zur Berechnung von
 . Die unabhängigen Parameter sollen dabei die
Gesamtenergie E und die Zeit
. Die unabhängigen Parameter sollen dabei die
Gesamtenergie E und die Zeit 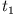 sein, zu der der Oszillator seinen Maximalausschlag erreicht.
sein, zu der der Oszillator seinen Maximalausschlag erreicht.
- c)
- Wählen Sie die Lösung nun so, dass E und
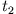 die unabhängigen Parameter sind,
wobei
die unabhängigen Parameter sind,
wobei 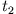 die Zeit ist, zu der der Oszillator seine maximale Geschwindigkeit annimmt.
die Zeit ist, zu der der Oszillator seine maximale Geschwindigkeit annimmt.

 Druckversion der Aufgaben
Druckversion der Aufgaben
 Druckversion der Lösungen
Druckversion der Lösungen
H.J. Lüdde, M. Keim
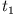 erreicht der Oszillator seinen Maximalausschlag
erreicht der Oszillator seinen Maximalausschlag 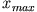 ? Wie groß ist
? Wie groß ist 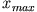 ? Welchen
Wert hat die Beschleunigung zur Zeit
? Welchen
Wert hat die Beschleunigung zur Zeit 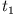 ?
?
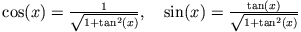
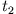 erreicht der Oszillator seine Maximalgeschwindigkeit
erreicht der Oszillator seine Maximalgeschwindigkeit
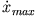 ? Wie groß ist
? Wie groß ist
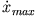 ? Wie groß ist die Auslenkung zur Zeit
? Wie groß ist die Auslenkung zur Zeit 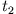 ? Welche einfache Beziehung besteht zwischen
? Welche einfache Beziehung besteht zwischen 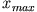 und
und
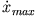 ?
?
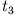 erfährt der Oszillator die maximale Beschleunigung
erfährt der Oszillator die maximale Beschleunigung
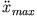 ? Wie groß ist
diese? Welche Werte haben Auslenkung und Geschwindigkeit zur Zeit
? Wie groß ist
diese? Welche Werte haben Auslenkung und Geschwindigkeit zur Zeit 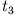 ?
?

 . Die unabhängigen Parameter sollen dabei die
Gesamtenergie E und die Zeit
. Die unabhängigen Parameter sollen dabei die
Gesamtenergie E und die Zeit 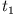 sein, zu der der Oszillator seinen Maximalausschlag erreicht.
sein, zu der der Oszillator seinen Maximalausschlag erreicht.
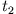 die unabhängigen Parameter sind,
wobei
die unabhängigen Parameter sind,
wobei 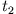 die Zeit ist, zu der der Oszillator seine maximale Geschwindigkeit annimmt.
die Zeit ist, zu der der Oszillator seine maximale Geschwindigkeit annimmt.