C++ Container und die vector Klasse der Standardbibliothek
Einführung
In der vorigen Vorlesung hatten wir in das C++ Klassenkonzept eingeführt, mit welchem der Programmierer einen eigenen benutzerdefinierten Typ erstellen kann. Bei vielen Programmier-Teilaufgaben innerhalb eines Programms ist es jedoch oft nicht nötig seine eigene Programmierstruktur zu entwerfen, da es in der C++ Standardbibliothek (STL: Standard Template Library) schon viele zusammengesetzte Strukturen gibt, die man einfach übernehmen kann. So ist es z.B. beim Rechnen mit komplexwertigen Zahlen nicht nötig seine eigene Klasse der komplexwertigen Zahlenmenge zu entwerfen, sondern man kann einfach mittels '#include <complex>' die Klasse der komplexwertigen Zahlen aus der C++ Standardbibliothek verwenden (siehe std::complex und weiter unten).
Die C++ Standardbibliothek verfügt über eine Vielzahl nützlicher Programmierkonstrukte und ein oft verwendetes Klassenkonzept sind die sogenannten C++ Container. Ein Container ist ein Objekt, das eine Sammlung von Elementen aufnimmt. Die verfügbaren STL-Container gliedern sich in sequentielle Container (wie z.B. '<vector>' und '<list>') und ungeordnete/geordnete assoziative Container (wie z.B. '<map>' und '<unordered_map>'). Wir werden nicht näher auf die feinen Unterschiede dieser unterschiedlichen Containervarianten eingehen und uns im Folgenden mit dem wohl wichtigsten Container <vector> näher befassen.
#include <iostream> // Ein- und Ausgabebibliothek // Beispiel fuer die Struktur der vector-Klasse der Standardbibliothek class Vektor { // Private Instanzvariablen (Daten-Member) private: double* elem; // Zeiger auf das eindimensionale Array von 'anz' double Elementen int anz; // Anzahl der Elemente des vector-Objektes // Oeffentliche Bereiche der Klasse public: // Ueberladene Konstruktoren der Klasse Vektor // Konstruktor mit einem Argument Vektor(int set_anz) : elem { new double[set_anz] }, anz{set_anz} { printf("Konstruktor(anz) erzeugt einen Vektor-Container mit %i Elementen \n", set_anz); for(int i = 0; i!=set_anz; ++i){ elem[i] = 0; } } //... // Destruktor der Klasse Vektor ~Vektor() { printf("Destruktor loescht den Vektor-Container \n"); delete[] elem; } // Oeffentliche Member-Funktionen der Klasse //... }; int main(){ // Hauptfunktion Vektor w = Vektor(3); // Deklaration eines Objektes der Vektor-Klasse mit drei Elementen }

Die Klassenstruktur des standard Containers <vector>
Der STL-Container <vector> der C++ Standardbibliothek stellt einen sequenziellen Typ von Objekten dar und ist somit eine Sequenz von Elementen eines bestimmten Typs. Bei der Definition eines vector-Objektes werden die einzelnen Elemente des Vektors, im Hauptspeicher aufeinanderfolgend abgelegt. Man kann sich die Struktur eines vector-Objektes als ein eindimensionales Array vorstellen, bei welchem man zusätzlich noch die Anzahl der Elemente im Programmverlauf verändern kann. Außerdem stellt die vector-Klasse mehrere Memberfunktionen bereit, die einem bei der Konstruktion des Vektors helfen. Die Vektorklasse ist als eine Template-Klasse formuliert, was bedeutet, dass der Typ T der Objekte veränderbar ist, die einzelnen Objekte jedoch von gleichem Typ sein müssen. Man erzeugt ein vector-Objekt, indem man einen der vector-Konstruktoren im Hauptprogramm aufruft (z.B. ' vector<T> v;').
Der grundlegende Aufbau der STL-vector-Klasse ähnelt der Vektor Klasse, die im nebenstehenden C++ Programm beispielhaft erstellt wurde. Der Konstruktor von Vektor alloziert mithilfe des Operators 'new double[set_anz]' Speicher im dynamischen Speicherbereich des Computers (Freispeicher, Heap). Am Ende, wenn das Objekt nicht mehr benötigt wird, gibt der Destruktor '~Vektor() { ... }' dann den benutzten Speicher wieder frei. Beim Aufruf des Konstruktors werden die privaten Instanzvariablen ( 'double* elem;' und 'int anz;') initialisiert und ein 'printf(...)' Befehl gibt im Terminal aus, dass der Konstruktor aufgerufen wurde. Im Hauptprogramm wird lediglich ein Objekt der vector-Klasse mit drei Elementen deklariert. Führt man das Programm aus, so erhält man die nebenstehende Terminalausgabe.
Im Folgenden werden wir den STL-vector-Container vorstellen und seine Verwendung erklären. Man kann diesen immer dann verwenden, wenn man ein eindimensionales Array im Programm deklarieren möchte, bei dem man die Dimension im Laufe des Programmes noch verändern kann. Der vector-Container hat gegenüber den integrierten Arrays (siehe C++ Arrays, Zeiger und Referenzen) noch weitere Vorteile und seine Verwendung in Funktionen ist, im Vergleich zu integrierten Arrays, ebenfalls einfacher.
Die Klasse <vector> am Beispiel eines Integer Vektors
In diesem Unterpunkt werden wir lernen, wie man einen vector-Container erstellt und ihn mit Elementen füllt. Dies werden wir am Beispiel eines Vektors, bestehend aus Integer-Zahlen machen. Im folgenden C++ Programm wird ein Integer vector-Objekt mittels der Anweisung 'vector<int> w = {1,4,6,8,9,5,3};' deklariert und gleichzeitig mit sieben Integer Zahlen initialisiert.
#include <iostream> // Ein- und Ausgabebibliothek #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek using namespace std; // Benutze den Namensraum std int main(){ // Hauptfunktion vector<int> w = {1,4,6,8,9,5,3}; // Deklaration und Initialisierung eines Integer-vector-Containers mit sieben Einträgen vector<int>::iterator Iter; // nur fuer Schleifen mit ::iterator noetig w.push_back(10); // Einfuegen eines neuen Elementes am Ende des Vektors printf("w = ("); for (auto& n : w){ // Bereichsbasierte for-Schleife zum Ausgeben der einzelnen Elemente des Vektors printf("%3i ", n); } printf(") \n \n"); w.insert(w.begin()+3,99); // Einfuegen eines neuen Elementes an der vierten Position des Vektors printf("w = ("); for ( Iter = w.begin() ; Iter != w.end() ; Iter++ ){ // for-Schleife zum Ausgeben der einzelnen Elemente des Vektors (mittels ::iterator) printf("%3i ", *Iter); } printf(") \n \n"); w[5] = 77; // Neue Wert-Zuweisung fuer das 6. Elementes des Vektors printf("w = ("); for(size_t i=0; i<w.size(); ++i){ // Normale for-Schleife zum Ausgeben der einzelnen Elemente des Vektors printf("%3i ", w[i]); } printf(") \n"); }

| Anweisung | Bedeutung |
|---|---|
| v.push_back(val); | Fügt die Daten aus val an das Ende des Vektors v an. |
| v.pop_back(); | Entfernt das letzte Element des Vektors v. |
| v.insert(pos,val); | Fügt die Daten aus val an die Position pos des Vektors v ein. |
| v.size(); | Gibt die Anzahl aller Elemente im Vektors v zurück. |
| v.resize(n); | Setzt die Anzahl der Elemente im Vektors auf n. |
| v.clear();. | Entfernt alle Elemente des Vektors v. |
| v.front(); | Gibt die Referenz auf das erste Element von v zurück. |
| v.back(); | Gibt die Referenz auf das letzte Element von v zurück. |
| v.capacity(); | Die Anzahl der Elemente die in v gespeichert werden können. |
| v.at(n); | Repräsentiert das n. Element des Vektors v (prüft zuvor, ob n im erlaubten Bereich liegt). |
| v[n]; | Repräsentiert das n. Element des Vektors v (prüft nicht, ob n im erlaubten Bereich liegt). |
Es werden danach verschiedene Operationen (Methoden, Member-Funktionen der Klasse vector) angewandt, um den definierten Vektor zu verändern. Der Vektor wird mittels drei unterschiedlicher Schleifenvarianten im Terminal ausgegeben, wobei eine dieser Varianten den speziellen vector-'::iterator' benutzt, der im Programm am Anfang schon deklariert wurde. Iteratoren stellen in C++ die idiomatische Art dar, um Positionen in Containern zu adressieren und sind besonders bei nicht-indexbasierten Containern (z.B. <list>) gebräuchlich. Die nebenstehende Abbildung zeigt die gesamte Terminalausgabe des Programms. Nach der Erzeugung des Vektors $w$ wird diesem ein zusätzliches Element (die Integer Zahl '10') hinzugefügt. Dieses Einfügen am Ende des Vektors wird mittels der Anweisung 'w.push_back(10);' gemacht. Der Vektor wird dann mittels einer bereichsbasierten for-Schleife im Terminal ausgegeben. Es wird dann, mittels der Anweisung 'w.insert(w.begin()+3,99);', nach dem dritten Element die Zahl '99' dem Vektor hinzugefügt. Der Vektor wird dann mittels einer for-Schleife im Terminal ausgegeben, die den Iterator vector-'::iterator' benutzt. Danach wird der Wert des sechsten Elementes des Vektors auf '77' abgeändert (w[5] = 77;) und der Vektor mittels einer 'normalen' for-Schleife ausgegeben. Der hierbei verwendete Index-Typ 'size_t' ist ein vorzeichenloser Ganzzahltyp, der für Container-Größen und Indizes in der Standardbibliothek verwendet wird.

Die nebenstehende Tabelle listet einige der verfügbaren Vektoroperatoren auf. Die Methode 'v.resize(n);' wird in dem unteren Quelltext des C++ Programms Vector_2.cpp benutzt. In dem Programm wurde zunächst ein Integer-Vektor $w$ mit fünf Elementen deklariert (vector<int> w(5);). Die fünf Elemente des Vektors erhalten dann, innerhalb einer for-Schleife, ihre entsprechenden Werte und der Vektor wird im Terminal ausgegeben. Dann wird der Vektor mittels 'w.resize(7);' auf eine Kapazität von sieben erhöht und die Wertzuweisungen an die neuen Elemente gemacht. Die Terminalausgabe des Programms (siehe rechte kleine Abbildung) zeigt die Erhöhung der Kapazität des Vektors.
#include <iostream> // Ein- und Ausgabebibliothek #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek using namespace std; // Benutze den Namensraum std int main(){ // Hauptfunktion vector<int> w(5); // Deklaration eines Integer-vector-Containers mit fuenf Einträgen for(size_t i = 0; i < w.size(); ++i){ // Normale for-Schleife zum Ausgeben der einzelnen Elemente des Vektors w[i] = i*i; // Wert-Zuweisung an das t-te Elementes des Vektors } printf("w = ("); for (auto& n : w){ // Bereichsbasierte for-Schleife zum Ausgeben der einzelnen Elemente des Vektors printf("%3i ", n); } printf(") \n"); w.resize(7); // Die Anzahl der Eintraege im Vektor w wird auf 7 erhoeht w[5] = 5*5; // Wert-Zuweisung an das 5-te Elementes des Vektors w[6] = 6*6; // Wert-Zuweisung an das 6-te Elementes des Vektors printf("w = ("); for (auto& n : w){ // Bereichsbasierte for-Schleife zum Ausgeben der einzelnen Elemente des Vektors printf("%3i ", n); } printf(") \n"); }
In gleicher Weise, wie man den vector-Container aus Integer-Zahlen erzeugt, kann man auch einen STL-vector aus Gleitkommazahlen erstellen (z.B. 'vector<double> w(5);'). Auch ist es möglich mehrdimensionale Matrix-ähnliche Konstrukte mittels einer geschachtelten vector-Container-Struktur zu deklarieren (siehe das C++ Programm Array_mehrdim_funktion_stdvector.cpp, welches bereits im Unterpunkt Mehrdimensionalen C++ Arrays in Vorlesung 6 besprochen wurde). In ähnlicher Weise wie bei den integrierten mehrdimensionalen C++ Arrays (siehe Vorlesung 6) ist dann auch ein Zugriff auf die Elemente des Arrays mittels einer, in der Physik gebräuchlichen Index-Schreibweise möglich.
Ein wichtiger Vorteil des vector-Containers gegenüber integrierten C++ Arrays besteht auch in seiner einfachen Verwendung im Kontext von Funktionen. STL-vector-Container können in einfacher Weise in der Argumentenliste von Funktionen verwendet werden und es ist ebenfalls möglich, sie als Rückgabetyp der Funktion zu verwenden. Im folgenden C++ Programm wurde z.B. eine Funktion definiert (vector<double> erzeugeEinheitsvektor(const vector<double>& v) {...}), die einen Einheitsvektor $e_v$ aus einem gegebenen Vektor $v$ berechnet. Der Typ des vector-Containers wird dabei sowohl in der Argumentenliste, als auch bei der Rückgabe verwendet. In der Hauptfunktion wird dann diese Funktion bei der Initialisierung eines vector-Containers benutzt: 'vector<double> e_w = erzeugeEinheitsvektor(w);'
#include <iostream> // Ein- und Ausgabebibliothek #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) using namespace std; // Benutze den Namensraum std // Funktion zur Berechnung des Einheitsvektors vector<double> erzeugeEinheitsvektor(const vector<double>& v) { // Berechnung des Betrages (Länge) des Vektors double laenge = 0.0; for (double vi : v) { laenge += vi * vi; } laenge = sqrt(laenge); // Erstelle Einheitsvektor mittels Division jeder Komponente durch die Länge vector<double> e_v(v.size(),0); if (laenge != 0.0) { // Nur möglich falls v kein Nullvektor ist for (size_t i = 0; i < v.size(); ++i) { e_v[i] = v[i]/laenge; } } return e_v; } // Hauptfunktion int main(){ // Deklaration und Initialisierung eines double-vector-Containers mit drei Einträgen vector<double> w = {3.2,4.0,-5.1}; // Deklaration des Einheitsvektors und Initialisierung mittels des Rückgabewertes der <vector>-Funktion erzeugeEinheitsvektor(w) vector<double> e_w = erzeugeEinheitsvektor(w); // Bereichsbasierte for-Schleife zum Ausgeben der einzelnen Elemente des Vektors printf("w = ("); for (auto& n : w){ printf("%6.3f ", n); } printf(") \n"); // Bereichsbasierte for-Schleife zum Ausgeben der einzelnen Elemente des Einheitsvektors printf("e_w = ("); for (auto& n : e_w){ printf("%6.3f ", n); } printf(") \n"); }
Beispiel: Die Mandelbrot-Menge (komplexwertige Vektoren und Vektor-Matrizen)
In diesem Unterpunkt werden wir einerseits die Klasse der komplexen Zahlen der C++ Standardbibliothek kennenlernen und andererseits sehen, wie man einen vector-Container bestehend aus komplexwertigen Zahlen erstellt. Am Ende betrachten wir die Mandelbrot-Menge und lernen das Konstrukt der Vektor-Matrizen der C++ Standardbibliothek kennen.
Die Mandelbrot-Menge gründet auf der folgenden, rekursiv definierten komplexwertigen Folge: \[ \begin{equation} z_{n+1} \,=\, (z_n)^2 + c \quad \forall \,\, c, z_n \in ℂ \, , \,\, n \in ℕ \quad , \end{equation} \] wobei der Anfangswert der Folge stets $z_0=0$ ist und $c \in ℂ$ eine beliebige komplexe Zahl darstellt. Betrachtet man sich die Folgenglieder $z_0, z_1, z_2, z_3, ...$, so divergieren diese für manche $c \in ℂ$, für andere $c$ bleibt die Folge jedoch auch für sehr große $n \in ℕ$ beschränkt. Wir wollen dies nun für zwei Beispiele explizit zeigen.
Das folgende C++ Programm berechnet z.B. die ersten 500 Folgenglieder bei einer Wahl von $c = 0.1 +i \cdot 0.1 \in ℂ$ und speichert diese in einem komplexwertigen vector-Container (vector<complex<double>> f;). Es werden dann die ersten 20 Folgenglieder und das letzte Folgenglied im Terminal ausgegeben (und zusätzlich ebenfalls die Größen $(z_n)^2$ und $|z_n|$).
#include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <complex> // Standardbibliothek fuer komplexwertige Zahlen using namespace std; // Benutze den Namensraum std int main() { vector<complex<double>> f; // Deklaration eines vector-Containers fuer komplexe Zahlen complex<double> c(0.1, 0.1); // Definition der komplexen Zahl c = 0.1 +i*0.1 (c(0.5, 0.1)) complex<double> z(0, 0); // Definition des Anfangswertes der komplexwertigen Folge const int iter_max = 500; // Maximal Wert der Iterationen for (int i = 0; i <= iter_max; ++i){ // for-Schleife ueber die ersten iter_max=500 Folgenwerte f.push_back(z); // Anfuegen eines neuen Folgenwertes an den komplexwertigen vector-Container z = z * z + c; // Bildungsgesetz der komplexwertigen Folge } // Ende for-Schleife // for-Schleife der Ausgabe ueber die ersten 20 Folgenwerte cout << "Iteration i " << "Folgenwert z[i] " << " z[i]*z[i] " << " |z[i]| " << endl; for (int i = 0; i < 20; ++i){ cout << i << " " << f[i] << " " << f[i]*f[i] << " " << abs(f[i]) << endl; } // und Ausgabe des letzten Folgenwertes cout << iter_max << " " << f[iter_max] << " " << f[iter_max]*f[iter_max] << " " << abs(f[iter_max]) << endl; }
Die Terminalausgabe des Programms für $c = 0.1 +i \cdot 0.1$ ist unten links und für $c = 0.5 +i \cdot 0.1$ unten rechts veranschaulicht.
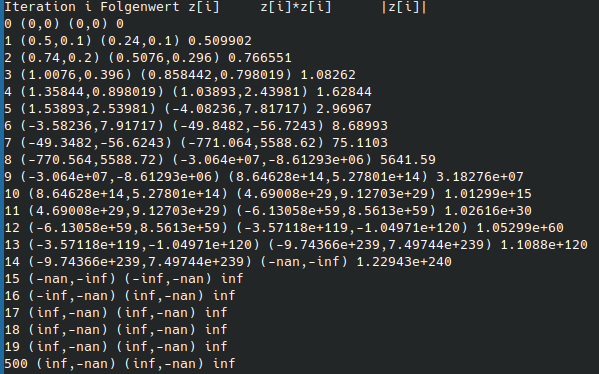
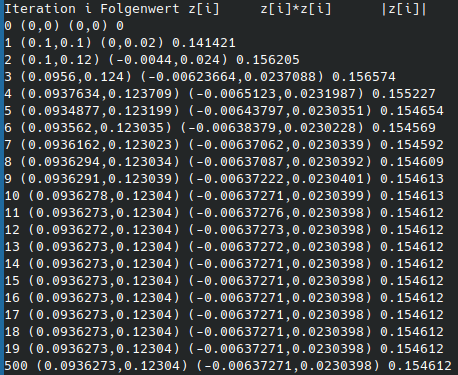
Man erkennt, dass die Folge mit $c = 0.1 +i \cdot 0.1$ einem komplexwertigen Fixpunkt zustrebt, wohingegen Folge mit $c = 0.5 +i \cdot 0.1$ divergiert. Es lässt sich nun mathematisch zeigen, dass falls der Betrag eines Folgengliedes größer als 2 ist ($|z_n| > 2$), die Folge dann nach kurzer Zeit divergieren muss. In der obigen Ausgabe sehen wir diese Eigenschaft ebenfalls.
Die Mandelbrot-Menge sind nun alle komplexen Zahlen $c \in ℂ$, für welche die oben definierte Folge beschränkt bleibt und nicht divergiert. Bei der Berechnung und Visualisierung der Mandelbrot-Menge teilt man den komplexwertigen Zahlenraum $ℂ$ in ein feinmaschiges Gitter auf und prüft für jede einzelne komplexwertige Zahl $c \in ℂ$, ob die Folge $z_n$ beschränkt bleibt, und falls nicht, merkt man sich den Wert der Iteration ab welchem die Folge divergiert (bzw. gleichbedeutend ab wann $|z_n| > 2$ auftritt). Die so berechnete Integer-Zahlenmatrix des komplexen Zahlenraumes stellt man sich dann grafisch dar, wobei die Größe der Divergenz-Iteration die jeweilige Farbe des komplexen Zahlenpunktes $c$ bestimmt.
Das folgende C++ Programm berechnet die Mandelbrot-Menge, indem sie den Raum der komplexen Zahlen $c = x +i \cdot y \in ℂ$ in $N \cdot N = 1000 \cdot 1000$ Gitterpunkte untergliedert und für jeden dieser Punkte prüft, ob die Folge divergiert. Damit das Programm nicht zu viel Zeit benötigt, wurde ein Maximalwert des Folgenindex definiert (const int iter_max = 100;) und die Abbruchbedingung der Folgenberechnung wurde mittels einer while-Schleife realisiert (while ( abs(z) <= 2.0 && iter < iter_max ) { ... }). Die gesamten Iterationswerte, ab welchen eine Divergenz der Folge auftrat, wurden in der Integer-Vektor-Matrix 'vector<vector<int>> output; ' gespeichert. Die berechneten Werte wurden am Ende im Terminal mittels einer bereichsbasierten for-Schleife ausgegeben.
/* Berechnung des Apfelmaenchens der Mandelbrot-Menge * Ausgabe zum Plotten mit Python mittels: "./a.out > Mandelbrot.dat" */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <complex> // Standardbibliothek fuer komplexwertige Zahlen using namespace std; // Benutze den Namensraum std int main() { const int iter_max = 100; // Maximal Wert der Iterationen // Bereich der komplexen Zahlen der Mandelbrotmenge const double x_min = -1.9; // Realteil Minumum const double x_max = 0.5; // Realteil Maximum const double y_min = -1.2; // Imaginaerteil Minumum const double y_max = 1.2; // Imaginaerteil Maximum const int N = 1000; // Anzahl der Punkte in die das xy-Intervall aufgeteilt wird const double h_x = (x_max - x_min)/N; // Abstand zwischen den aequidistanten Punkten des x-Intervalls const double h_y = (y_max - y_min)/N; // Abstand zwischen den aequidistanten Punkten des y-Intervalls vector<vector<int>> output; // Deklaration eine int Vektor-Matrix zum speichern der Loesungen for (int k = 0; k < N; ++k) { // for-Schleife ueber die Punkte des x-Intervalls vector<int> output_k; // Lokaler int Vektor fuer jeden k-Wert for (int l = 0; l < N; ++l) { // for-Schleife ueber die Punkte des y-Intervalls complex<double> c( x_min + k*h_x , y_min + l*h_y); // Definition der komplexen Zahl c = x +i*y complex<double> z(0, 0); // Definition des Anfangswertes der komplexwertigen Folge // Iteration fuer die Mandelbrotmenge int iter = 0; // Iterationen, die benoetigt werden bis |z|>2 while ( abs(z) <= 2.0 && iter < iter_max ) { // while-Schleife ueber die einzelnen Folgenwerte z = z * z + c; // Bildungsgesetz der komplexwertigen Folge iter++; // Benoetigte Iteration + 1 } // Ende while-Schleife output_k.push_back(iter); // Anfuegen eines neuen Iterationswertes an den lokalen int vector-Container } // Ende for-Schleife y-Intervalls output.push_back(output_k); // Anfuegen eines neuen lokalen int vector-Containers an die int Vektor-Matrix } // Ende for-Schleife x-Intervalls // Ausgabe der Loesungswerte mittels einer bereichsbasierten for-Schleife for (const auto& output_k : output) { for (const int wert : output_k) { cout << wert << " "; } cout << endl; } }
Mit dem folgenden Python-Skript wurden dann die berechneten Daten geplottet.
# Python Programm zum Plotten der berechneten Daten von (Mandelbrot.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import matplotlib import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) # Festlegung einiger Bildparameter params = { 'figure.figsize' : [12,8], 'axes.titlesize' : 14, 'axes.labelsize' : 16, 'xtick.labelsize' : 14 , 'ytick.labelsize' : 14 } matplotlib.rcParams.update(params) data = np.genfromtxt("./Mandelbrot.dat") # Einlesen der berechneten Daten von Mandelbrot.cpp # Bereich der komplexen Zahlen der Mandelbrotmenge x_min = -1.9; x_max = 0.5; y_min = -1.2; y_max = 1.2; plt.imshow(data, extent=[y_min, y_max, x_max, x_min], cmap=plt.cm.nipy_spectral_r) # Plotten der Daten # Farbskala, Titel und Labels plt.colorbar(label='Iterationen') plt.title('Mandelbrotmenge') plt.ylabel('x=Re(c)') plt.xlabel('y=Im(c)') # Speichern der Abbildung als Bild plt.savefig("Mandelbrot.png", dpi=200,bbox_inches="tight",pad_inches=0.05,format="png") plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
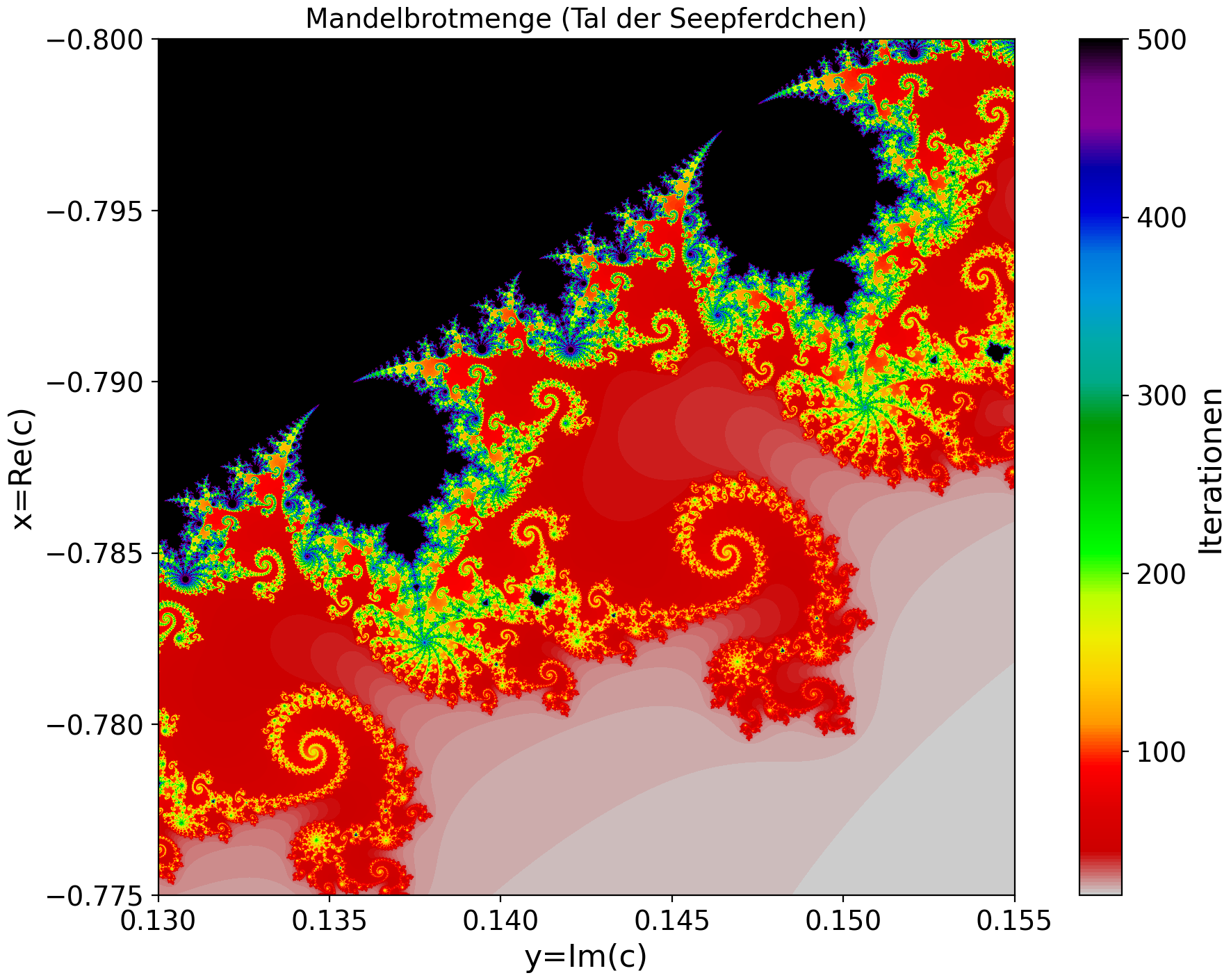

Die Abbildung oben links zeigt den gesamten Bereich der Mandelbrot-Menge (Re(c)$=x \in [-1.9,0.5]$ und Im(c)$=y \in [-1.2,1.2]$) und stellt das sogenannte Mandelbrot-Apfelmännchen dar. Die Abbildung oben rechts hingegen zeigt einen Zoom der Mandelbrot-Menge in den Bereich des sogenannten Tals der Seepferdchen (Re(c)$=x \in [-0.8,-0.775]$ und Im(c)$=y \in [0.13,0.155]$) und wurde mit 'const int iter_max = 500;' erstellt, um die feineren Strukturen genau abbilden zu können.
Die Klasse <vector> als ein Container von Objekten
Wie wir in den vorigen Unterpunkten gesehen haben, kann man die Klasse <vector> benutzen, um eindimensionale bzw. mehrdimensionale Arrays in Form von Standardvektoren darzustellen. Die Verwendung von einem vector-Objekt anstelle von einem integrierten Array hat den Vorteil, dass man die Kapazität des Vektors im Laufe des Programms einfach verändern kann. In diesem Unterpunkt wollen wir einen weiteren Anwendungsfall der Klasse <vector> betrachten, bei dem die Elemente des Containers selbst Objekte von Klassen sind. Betrachten wir z.B. die in der vorigen Vorlesung entworfene Klasse 'Ding' und stellen uns vor, dass wir eine bestimmte Anzahl von Dingen in eine Kiste einsperren möchten. Im folgenden Programm werden wir dies realisieren, indem wir einen Container, bestehend aus Objekten der Klasse 'Ding' erstellen (siehe Vorlesung 7, Unterpunkt Objekt-orientierte Programmierung und C++ Klassen).
Wir möchten im Folgenden eine gewisse Anzahl von Teilchen (z.B. unsigned int Anz_Teilchen = 10;) in eine zweidimensionale Kiste einsperren (Abmessung der Kiste z.B. double kiste_x = 40; und double kiste_y = 40; ). Die 10 Teilchen sollen im Hauptprogramm als Instanzen der Klasse Ding erzeugt werden, wobei wir uns hierbei an der in der Vorlesung 7 dargestellten Ding-Klasse orientieren. Im Gegensatz zu der im Programm Klasse_1a.cpp konstruierten Klasse, werden wir jedoch alle Merkmale der Klasse als öffentlich kennzeichnen und neben den Ortskoordinaten werden wir auch die Teilchengeschwindigkeiten als Daten-Member deklarieren. Mittels des Konstruktors kann der Benutzer die Nummer, die Anfangsorte und Anfangsgeschwindigkeiten der einzelnen Teilchen festlegen, wobei die Standardinitialisierungen zunächst auf null initialisiert werden. Da alle Instanzvariablen öffentlich zugänglich sind, werden die im Programm Klasse_1a.cpp verwendeten Member-Funktionen des 'Geheimnisprinzip' (z.B. 'double get_Ort() const {return x;}') nicht mehr benötigt.
Nun wird zusätzlich noch das zeitliche Verhalten der Dinge als eine inline Funktion definiert. Die Teilchen sollen hierbei zunächst nicht miteinander wechselwirken. Die Begrenzungen der Kiste bilden jedoch nicht überwindbare Barrieren für die klassischen Teilchen und es soll eine vollständige Reflexion an den Kistenbegrenzungen stattfinden. Wir implementieren dieses zeitliche Verhalten der Teilchen als eine inline-Methode der Klasse 'Ding' und benennen sie 'Gehe_Zeitschritt': inline void Ding::Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z){ ... } . Die Funktion beschreibt die Veränderung der Ortskoordinaten $(x,y,z)$ bei einem Zeitschritt $dt$, wobei die speziellen Randbedingungen an die Bewegung der Teilchen (Reflexion an den Rändern der Kiste) mittels der Argumente double max_x, double max_y, double max_z spezifiziert werden.
Im Hauptprogramm wird dann ein vector-Container bestehend aus Objekten des benutzerdefinierten Typs '<Ding>' deklariert ( vector<Ding> Kiste_Teilchen; ) und dieser wird mittels der Anweisung 'Kiste_Teilchen.push_back( Ding {...} );' aufgefüllt. Nach diesem Initialisierungsprozess wird die zeitliche Entwicklung der Teilchen für z.B. 100 Zeitschritte (double Anz_tSchritte = 100; mit double dt = 0.05;) im Terminal ausgegeben. Das folgende C++ Programm stellt eine Realisierung des vector-Containers bestehend aus 10 Dingen mit zeitlicher Entwicklung der Ortskoordinaten dar.
/* Beispiel fuer einen Vector-Container bestehend aus mehreren Elementen des Typs Ding * Ding ist eine Klasse die ausschliesslich aus oeffentlichen Merkmalen besteht * sieben Instanzvariablen (Nummer, Ort und Geschwindigkeit des Dings in 3D) * ein Konstruktor mit sieben Argumenten * eine Member-Funktionen Member-Funktionen 'Gehe_Zeitschritt', * die eine zeitliche Entwicklung im Programm implementiert * Ausgabe zum Plotten (Python) mittels: "./a.out > Vector_Dinge.dat" * python3 PythonPlot_Vector_Dinge.py */ #include <iostream> // Ein- und Ausgabebibliothek #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek using namespace std; // Benutze den Namensraum std //Definition der Klasse 'Ding' class Ding{ // Oeffentliche Klasse public: // Instanzvariablen (Daten-Member) der Klasse unsigned int n; // Nummer des Dinges double x, y, z; // Ort des Dinges double v_x, v_y, v_z; // Geschwindigkeit des Dinges // Konstruktor mit sieben Argumenten und Standardinitialisierungen Ding(unsigned int set_n = 0, double set_x = 0.0, double set_y = 0.0, double set_z = 0.0, double set_v_x = 0.0, double set_v_y = 0.0, double set_v_z = 0.0) : n{set_n}, x{set_x}, y{set_y}, z{set_z}, v_x{set_v_x}, v_y{set_v_y}, v_z{set_v_z} {} // Member-Funktionen der Klasse void Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z); // Deklaration einer Member-Funktion (Definition findet ausserhalb der Klasse statt) }; /* Definition der Funktion Gehe_Zeitschritt(...) als inline-Methode der Klasse Ding * Die Funktion beschreibt die Veränderung der Ortskoordinaten (x,y,z) bei einem Zeitschritt dt * Es sind zusaetzlich spezielle Randbedingungen an die Bewegung formuliert, so dass sich die * Dinge nur in einem Bereich von [0,max_x], [0,max_y] und [0,max_z] bewegen koennen */ inline void Ding::Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z){ x += v_x * dt; y += v_y * dt; z += v_z * dt; if (x >= max_x || x <= 0){v_x = - v_x;} if (y >= max_y || y <= 0){v_y = - v_y;} if (z >= max_z || z <= 0){v_z = - v_z;} } int main(){ // Hauptfunktion double kiste_x = 40; // Laenge der Kiste double kiste_y = 40; // Breite der Kiste unsigned int Anz_Teilchen = 10; // Definition der Anzahl der zu erzeugenden Dinge double t; // Deklaration des Zeitparameters double dt = 0.05; // Definition der Laenge des Zeitschrittes double Anz_tSchritte = 100; // Anzahl der Zeitschritte vector<Ding> Kiste_Teilchen; // Deklaration eines vector-Containers for (unsigned int n = 0; n < Anz_Teilchen; ++n){ // for-Schleife zum Auffuellen des Containers mit Elementen vom Typ 'Ding' Kiste_Teilchen.push_back( Ding {n, 1, (n+1)*kiste_y/Anz_Teilchen, 0, (n+1.0), 0, 0} ); // Initialisierung: Nur in x-y-Ebene, Geschwindigkeit nur in x-Richtung } printf("# 0: Index i \n# 1: Zeit t \n# 2: Nummer des Teilchens 1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: x-Position des Teilchens 1 \n# 4: y-Position des Teilchens 1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 5: Nummer des Teilchens 2 \n# 6: .... bis Anzahl der Teichen \n"); // Beschreibung der ausgegebenen Groessen for (int i = 0; i < Anz_tSchritte; ++i){ // for-Schleife fuer die zeitliche Entwicklung der Dinge in der Kiste t = i * dt; // Zeit geht in dt-Schritten voran printf("%3i %10.6f ", i, t); // Ausgabe Index i und Zeit t for (auto& j : Kiste_Teilchen){ // Bereichsbasierte for-Schleife zum Ausgeben der x-y-Orte der Dinge printf("%3i %10.6f %10.6f ", j.n, j.x, j.y); // Ausgabe Teilchenorte j.Gehe_Zeitschritt(dt,kiste_x, kiste_y, 0.0); // Aufruf der inline Funktion Gehe_Zeitschritt(...) } printf("\n"); } }
Die nebenstehende Animation visualisiert die produzierten Daten des C++ Programmes und wurde mittels eines Jupyter Notebooks erstellt (näheres siehe weiter unten). Nachdem der vector-Container mit dem Namen 'Kiste_Teilchen' mittels 'vector<Ding> Kiste_Teilchen;' deklariert ist, wird er in der folgenden for-Schleife mit 10 Ding-Objekten aufgefüllt.
for (unsigned int n = 0; n < Anz_Teilchen; ++n){
Kiste_Teilchen.push_back( Ding {n, 1, (n+1)*kiste_x/Anz_Teilchen, 0, (n+1.0), 0, 0} );
}
Die eigentliche Instanzbildung der Dinge wird mittels des Konstruktors realisiert: 'Ding { Argumentenliste des aufgerufenen Konstruktors }'. Hier wurde der Konstruktor mit allen sieben Argumenten gewählt ( Ding(Nummer,x,y,z,vx,vy,vz) ), bei dem die Teilchennummer, der Ort und die Geschwindigkeit des Teilchens individuell initialisiert wird. Die gewählte Anfangskonfiguration der Teilchen entspricht einer Teilchenbewegung in x-Richtung, wobei alle Teilchen bei x=1 und z=0 starten und ihre y-Postion äquidistant variiert. Die Teilchen mit einer hohen Teilchennummer n bewegen sich schneller als die Teilchen mit niedriger Nummer.
Die zeitliche Entwicklung des Systems wird durch die for-Schleife
'for (int i = 0; i < Anz_tSchritte; ++i){ ... }'
eingeleitet. In dieser Schleife wird die Zeitvariable t in äquidistanten Zeitschritten dt iterativ erhöht (t = i * dt;). Zu jedem Zeitschritt wird jedes Teilchen einzeln zeitlich entwickelt, indem die Member-Funktion 'Gehe_Zeitschritt' aufgerufen wird:
j.Gehe_Zeitschritt(dt,kiste_x, kiste_y, 0.0);
Zusätzlich werden für jedes Teilchen, seine Nummer und seine aktuelle x- und y-Position ausgegeben. Leitet man die Terminalausgabe in die externe Datei 'Vector_Dinge.dat' um und benutzt das unten abgebildete Python Skript PythonPlot_Vector_Dinge.py, so kann man sich die Bewegung der Teilchen als eine Abfolge von Bildern visualisieren und diese Bilder bilden die Grundlage des oben abgebildeten Videos. Beachten Sie, dass man bevor man das Python-Programm startet, einen Unterordner 'Bilder' erstellt haben muss, indem die einzelnen Bilder gespeichert werden.
# Python Programm zum Plotten der Daten des Vector-Containers mit 10 Dingen (Vector_Dinge.cpp) # Es werden hier mehrere Bilder der zeitlichen Entwicklung des Systems in einem Ordner 'Bilder' gespeichert # !!!! Sie muessen vor der Ausfuehrung des Programms den Ordner Bilder erstellen !!!! # Die einzelnen Bilder kann mann dann mittels des folgenden Terminalbefehls zu einem Video binden: # ffmpeg -framerate 5 -i './Vector_Dinge_%03d.png' -c:v libx264 Vector_Dinge.mp4 import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./Vector_Dinge.dat") # Einlesen der berechneten Daten von Vector_Dinge.cpp plt.title(r'Container mit Teilchen') # Titel der Abbildung plt.ylabel('y') # Beschriftung y-Achse plt.xlabel('x') # Beschriftung x-Achse r = 200 # Radius eines Dings plot_min=0 # Festlegung der x-Untergrenze (Abmessung Kiste) plot_max=40 # Festlegung der x-Obergrenze (Abmessung Kiste) anz_teilchen = 10 # Definition der Anzahl der Dinge cmap = plt.cm.Blues # Definition der Farbschattierung der Dinge line_colors = cmap (np.linspace(0.2,1,anz_teilchen)) # Definition der Farbschattierung der Dinge for it in range(len(data[:,0])): # for-Schleife fuer die zeitliche Entwicklung der Dinge in der Kiste print(it) # Terminalausgabe der Erstellung des i-ten Bildes plt.cla() for i in range(anz_teilchen): # for-Schleife ueber die Teilchen in der Kiste plt.scatter(data[it,3*i+3],data[it,3*i+4], marker='o', color=line_colors[i], s=r) # Kennzeichnung der Position des Dinges durch einen blauen Kreis plt.text(data[it,3*i+3],data[it,3*i+4], str(int(data[it,3*i+2])), fontsize=10, verticalalignment='center', horizontalalignment='center', color="red") # Ding Nr. plt.xlim(-1,45) # Plot-Limit x-Achse plt.ylim(-1,45) # Plot-Limit y-Achse # Bild-Ausgabe mit Speicherung eines individuellen Iteration-Namens pic_name = "./Bilder/" + "Vector_Dinge_" + "{:0>3d}".format(it) + ".png" plt.savefig(pic_name, dpi=100,bbox_inches="tight",pad_inches=0.05,format="png") plt.close()
Wir möchten nun kleine Abänderungen in den Anfangsbedingungen der Teilchen machen. Die Größe der Kiste soll jetzt den Abmessungen des Leitbildes der Vorlesung illustration_DeborahMoldawski.jpg entsprechen und es werden 30 Teilchen in diese Kiste eingesperrt. Die Teilchen sollen am Anfang auf der linken Seite auf mittlerer Höhe starten und sich dann in unterschiedlicher Weise nach rechts bewegen. Das folgende C++ Programm stellt eine solche Teilchenentwicklung dar.
/* Beispiel fuer einen Vector-Container bestehend aus mehreren Elementen des Typs Ding * Ding ist eine Klasse die ausschliesslich aus oeffentlichen Merkmalen besteht * sieben Instanzvariablen (Nummer, Ort und Geschwindigkeit des Dings in 3D) * ein Konstruktor mit sieben Argumenten * eine Member-Funktionen Member-Funktionen 'Gehe_Zeitschritt', * die eine zeitliche Entwicklung im Programm implementiert * Initialisierung der Dinge und Abmessung der Kiste wurden an die * Einbindung eines Hintergrundbildes angepasst * Ausgabe zum Plotten (Python) mittels: "./a.out > Vector_Dingea.dat" * python3 PythonPlot_Vector_Dingea.py */ #include <iostream> // Ein- und Ausgabebibliothek #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) using namespace std; // Benutze den Namensraum std //Definition der Klasse 'Ding' class Ding{ // Oeffentliche Klasse public: // Instanzvariablen (Daten-Member) der Klasse unsigned int n; // Nummer des Dinges double x, y, z; // Ort des Dinges double v_x, v_y, v_z; // Geschwindigkeit des Dinges // Konstruktor mit sieben Argumenten und Standardinitialisierungen Ding(unsigned int set_n = 0, double set_x = 0.0, double set_y = 0.0, double set_z = 0.0, double set_v_x = 0.0, double set_v_y = 0.0, double set_v_z = 0.0) : n{set_n}, x{set_x}, y{set_y}, z{set_z}, v_x{set_v_x}, v_y{set_v_y}, v_z{set_v_z} {} // Member-Funktionen der Klasse void Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z); // Deklaration einer Member-Funktion (Definition findet ausserhalb der Klasse statt) }; /* Definition der Funktion Gehe_Zeitschritt(...) als inline-Methode der Klasse Ding * Die Funktion beschreibt die Veränderung der Ortskoordinaten (x,y,z) bei einem Zeitschritt dt * Es sind zusaetzlich spezielle Randbedingungen an die Bewegung formuliert, so dass sich die * Dinge nur in einem Bereich von [90,max_x], [90,max_y] und [90,max_z] bewegen koennen */ inline void Ding::Gehe_Zeitschritt(double dt, double max_x, double max_y, double max_z){ x += v_x * dt; y += v_y * dt; z += v_z * dt; if (x >= max_x || x <= 90){v_x = - v_x;} if (y >= max_y || y <= 90){v_y = - v_y;} if (z >= max_z || z <= 90){v_z = - v_z;} } int main(){ // Hauptfunktion double kiste_x = 5334 - 200; // Laenge der Kiste (ein wenig kuerzer als die Abmessung des Bildes) double kiste_y = 4000 - 200; // Breite der Kiste (ein wenig kuerzer als die Abmessung des Bildes) unsigned int Anz_Teilchen = 30; // Definition der Anzahl der zu erzeugenden Dinge double t; // Deklaration des Zeitparameters double dt = 0.01; // Definition der Laenge des Zeitschrittes double Anz_tSchritte = 200; // Anzahl der Zeitschritte vector<Ding> Kiste_Teilchen; // Deklaration eines vector-Containers for (unsigned int n = 0; n < Anz_Teilchen; ++n){ // for-Schleife zum Auffuellen des Containers mit Elementen vom Typ 'Ding' Kiste_Teilchen.push_back( Ding {n, 100, kiste_y/2, 0, kiste_x/2 + kiste_x*pow(sin(n),2), kiste_y*sin(2*M_PI*n/Anz_Teilchen)/2 , 0} ); } printf("# 0: Index i \n# 1: Zeit t \n# 2: Nummer des Teilchens 1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: x-Position des Teilchens 1 \n# 4: y-Position des Teilchens 1 \n"); // Beschreibung der ausgegebenen Groessen printf("# 5: Nummer des Teilchens 2 \n# 6: .... bis Anzahl der Teichen \n"); // Beschreibung der ausgegebenen Groessen for (int i = 0; i < Anz_tSchritte; ++i){ // for-Schleife fuer die zeitliche Entwicklung der Dinge in der Kiste t = i * dt; // Zeit geht in dt-Schritten voran printf("%3i %10.6f ", i, t); // Ausgabe Index i und Zeit t for (auto& j : Kiste_Teilchen){ // Bereichsbasierte for-Schleife zum Ausgeben der x-y-Orte der Dinge printf("%3i %10.6f %10.6f ", j.n, j.x, j.y); // Ausgabe Teilchenorte j.Gehe_Zeitschritt(dt,kiste_x, kiste_y, 0.0); // Aufruf der inline Funktion Gehe_Zeitschritt(...) } printf("\n"); } }
Man kann sich die Entwicklung nun wieder grafisch mittels des Python-Skriptes PythonPlot_Vector_Dingea.py veranschaulichen. Das unten abgebildete Video wurde mittels des Jupyter Notebooks Vector_Dinge.ipynb erstellt (siehe Vector_Dinge.html für den HTML-Export des Notebooks).