Objekt-orientierte Programmierung und C++ Klassen
Einführung
Die C++ Typen, die wir bisher kennengelernt hatten (z.B. int i, double a, int v[3], double A[4][5]), die sogenannten integrierten Typen, werden wir nun mittels eines Abstraktionsmechanismus erweitern, um eigenen, benutzerdefinierte Typen zu erstellen. Ein benutzerdefinierter Typ, wie z.B. die C++ Struktur 'struct' oder die C++ Klasse 'class', ist ein Abstraktionskonzept, das den Quelltext eines C+ Programms übersichtlicher macht, indem es das Programm in voneinander separierbare Teilbereiche aufteilt. Große Programme bestehen oft aus einzelnen Teilaufgaben, die man mittels einer sinnvollen Klassenstruktur voneinander trennen und ordnen kann. Eine C++ Klasse ist ein benutzerdefinierter neuer Datentyp, der durch das Schlüsselwort 'class' gekennzeichnet wird und die gesamte Idee der objektorientierten Programmierung beruht gänzlich auf diesem Konzept der Klasse.
Benutzerdefinierte Typen und Abstraktionsmechanismen in C++
Das Konzept der objektorientierten Programmierung beruht auf der alltäglichen Erfahrung, dass man Objekte nach zwei Maßstäben beurteilt: Ein Objekt besitzt einerseits messbare Eigenschaften (z.B. Farbe, Gewicht, ...) und ist aber auch andererseits über seine Verhaltensweisen (z.B. zeitliches Verhalten, Interaktionsverhalten, Bewegungsverhalten, ...) definiert. Eine Klasse ist ein abstrakter Oberbegriff für die Beschreibung der gemeinsamen Struktur und des gemeinsamen Verhaltens von realen/fiktiven Objekten (Klassifizierung). Mittels des Konzeptes der Klasse lassen sich solche Objekte im Programm realisieren. Eine Klasse stellt dabei den Bauplan für das zu beschreibende Objekt bereit und die wirkliche Realisierung des Objektes (die Instanzbildung) findet dann im Hauptprogramm zur Laufzeit statt. Eine Klasse stellt somit eine formale Beschreibung dar, wie das Objekt beschaffen ist, d.h. welche Merkmale (Instanzvariablen bzw. Daten-Member der Klasse) und Verhaltensweisen (Methoden der Klasse bzw. Member-Funktionen) das zu beschreibende Objekt hat. Eine Klasse ist also eine Vorlage, eine abstrakte Idee, die ein Grundgerüst von Eigenschaften und Methoden vorgibt. Die Erzeugung eines Objektes dieser Klasse entspricht der Materialisierung dieser Idee im Programm. Bei der Erzeugung des Objektes wird der sogenannte Konstruktor der Klasse aufgerufen, und verlässt das Objekt den Gültigkeitsbereich seines Teilbereiches des Programms, wird es durch den sogenannten Destruktor wieder zerstört. Das Grundgerüst einer Klasse besitzt die folgende Form, wobei im Anweisungsblock der Klasse nicht alle der aufgezählten Größen definiert werden müssen.
C++ Klassen: Zugriffskontrolle und die öffentlich zugänglichen Bereichen eines Objektes
class Klassenname {
// Private Instanzvariablen (Daten-Member) der Klasse
...
// Oeffentliche Konstruktoren und Member-Funktionen der Klasse
public:
// Standard-Konstruktor und überladene Konstruktoren der Klasse
...
// Member-Funktionen der Klasse
...
};
Eine weitere wichtige Klassen-Terminologie ist die Kennzeichnung von privaten und öffentlich zugänglichen Bereichen des Objektes. In einer Klasse werden die Daten-Member und Member-Funktionen nach außen gekapselt, sodass der Benutzer der Klasse sie nicht manipulieren kann (private-Bereiche der Klasse). Kennzeichnet man einen Bereich der Klasse jedoch als public, so kann man von außen auf die Daten und Methoden zugreifen und sie auch verändern. Neben diesen beiden Klassifizierungsbegriffen gibt es zusätzlich die Kennzeichnung protected. Besitzt eine Klasse keine explizite Kennzeichnung von privaten und öffentlich zugänglichen Bereichen, so sind alle Merkmale der Klasse privat. Bei der Verwendung der C++ Struktur 'struct' sind hingegen alle Merkmale öffentlich und man kann 'struct' somit als eine öffentliche 'class' ansehen. Die nebenstehende Abbildung veranschaulicht die Schreibweise einer C++ Klasse im Quellcode, wobei gewöhnlicherweise zunächst die privaten und dann die als öffentlich gekennzeichneten Definitionen und Anweisungen folgen.
Merkmale von C++ Klassen: Daten-Member und Member-Funktionen
Daten und Funktionen, die in einer Klassendefinition deklariert werden, bezeichnet man als Daten-Member (Instanzvariablen) und Member-Funktionen (Klassen-interne Funktionen). Durch die Bezeichner private, protected und public findet eine Kapselung der Klassen-internen Merkmale von den anderen Bereichen des C++ Programmes statt. Der Zugriff auf die privaten Eigenschaften des Objektes kann jedoch mittels konstanter, öffentlicher Zugriffsmethoden (Member-Funktionen) erfolgen. Durch diese Kapselung findet eine Art 'Information Hiding' statt ('Geheimnisprinzip' der Klasse).
Konstruktoren und Destruktoren
Möchte man ein Objekt der Klasse im Hauptprogramm erzeugen, so deklariert man es mit dem Klassennamen, gibt dem Objekt einen eigenen Namen und initialisiert am besten gleichzeitig die Instanzvariablen des Objektes. In einer Klasse gibt es dafür eine besondere Member-Funktion, der sogenannte Konstruktor. In einer Klasse kann es mehrere überladene Konstruktoren geben, die z.B. unterschiedliche Initialisierungsvarianten beschreiben. Ein Konstruktor ist eine öffentlich zugängliche Member-Funktion der Klasse, die im Gegensatz zu den anderen Klassen-Funktionen keinen Rückgabetyp besitzt und der Funktionsname des Konstruktors ist identisch mit dem Namen der Klasse. Verlässt das Objekt den Gültigkeitsbereich seiner Deklaration, bzw. spätestens bei Beendigung der main()-Funktion, wird das Objekt mittels des Destruktors zerstört. Manche Klassen benötigen die explizite Angabe eines Destruktors, um z.B. reservierte und benötigte Speicherbereiche freizugeben. Der Name des Destruktors besteht aus einer 'Tilde' ($\sim$) gefolgt von seinem Klassennamen.
Arten von Klassen: Konkrete und abstrakte Klassen
Allgemein ist eine Klasse ein benutzerdefinierter Typ mit der Aufgabe, ein Konzept im Code eines Programms darzustellen. Ein auf objektorientierten Prinzipien aufgebauter Quelltext, in welchem die wesentlichen Kernkonzepte und Ideen des Programms durch einen gut ausgewählten Satz von Klassen formuliert sind, ist wesentlich einfacher zu verstehen. Man unterscheidet hierbei grob die folgenden Arten von Klassen: die konkreten und abstrakte Klassen. Konkrete Klassen sind Klassen, die eine spezielle, konkrete Idee des Programms bzw. eine getrennt beschreibbare Teil-Entität des Quelltextes in einer Klasse zusammenfassend definiert. Bei konkrete Klassen ist die Darstellung der Kernidee in Form von C++ Anweisungen Teil der Klasse selbst und die Objekte der Klasse können sofort und vollständig von der Klasse initialisiert werden. Abstrakte Klassen hingegen stellen eine Art von Schnittstelle dar und sie entkoppeln die eigentliche Darstellung der konkreten Umsetzung der Idee von der Klasse. Oft werden abstrakte Klassen benutzt, um eine generelle Überstruktur des Programms zu definieren und mehrere Klassen miteinander in Verbindung zu bringen. Der Begriff der virtuellen Funktion hat bei der Formulierung von abstrakten Klassen einen wichtigen Stellenwert und solche Funktionen werden mit dem Zusatz 'virtual' gekennzeichnet; was besagt, dass sie in einer von dieser abstrakten Klasse abgeleiteten Unterklasse redefiniert werden.
Klassenhierarchien und die Vererbung von Klassenmerkmalen
C++ Klassen stehen häufig in Beziehung zueinander. Man hat beispielsweise eine Oberklasse (z.B. Kuchen), und aus dieser leitet sich eine andere Klasse (z.B. Brombeerkuchen) ab. Diese abgeleitete Klasse erbt dann bestimmte Eigenschaften der Daten-Member und Member-Funktionen der Oberklasse. In umfangreichen C++ Programmen baut sich somit eine Art von Klassenhierarchie auf und oft werden dabei auch sogenannte Templates eingesetzt, auf die wir erst in einer späteren Vorlesung eingehen werden.
Ein einfaches Beispiel für eine konkrete Klasse
Wir möchten nun eine einfache Klasse von Objekten/Dingen erstellen, wobei jedes Objekt eine ganzzahlige positive Nummer $n$ und eine Positionsangabe im Raum (eindimensionaler Raum mit Koordinate $x$) erhält. Diese Merkmale stellen die Instanzvariablen (Daten-Member) der Klasse dar und wir werden diese als private Daten deklarieren. Wir wählen als Klassenname 'Ding' und die Erzeugung der Objekte erfolgt mittels eines der drei überladenen Konstruktoren der Klasse:
Ding(unsigned int set_n) : n{set_n}, x{0} { ... }
Ding() : n{0}, x{0} { ... }
Die einzelnen Konstruktoren folgen der Schreibweise " 'Name der Klasse' ( 'Argumentenliste' ) : 'Initialisierung der Instanzvariablen mittels der Argumentenliste' { 'Anweisungsblock' } und unterscheiden sich lediglich in der 'Argumentenliste'. Die Auswahl, welcher der Konstruktoren bei der Erzeugung des Objektes benutzt wird, ist dem Benutzer überlassen. Das folgende Programm zeigt die Implementierung der Klasse und ihre Anwendung in der main()-Funktion des Programms:
/* Beispiel einer einfachen Klasse * Zwei private Instanzvariablen, * drei ueberladene Konstruktoren * Zwei oeffentliche Member-Funktionen */ #include <iostream> // Ein- und Ausgabebibliothek //Definition der Klasse 'Ding' class Ding{ // Private Instanzvariablen (Daten-Member) der Klasse unsigned int n; double x; // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Drei ueberladene Konstruktoren der Klasse // Konstruktor mit zwei Argumenten Ding(unsigned int set_n, double set_x) : n{set_n}, x{set_x} { printf("Konstruktor(n,x) erzeugt ein neues Ding \n"); } // Konstruktor mit einem Argument Ding(unsigned int set_n) : n{set_n}, x{0} { printf("Konstruktor(n) erzeugt ein neues Ding \n"); } // Konstruktor ohne Argument (Standard-Konstruktor) Ding() : n{0}, x{0} { printf("Konstruktor() erzeugt ein neues Ding \n"); } // Member-Funktionen der Klasse // als const deklariert, da sie die privaten Instanzvariablen nicht veraendern unsigned int get_Nummer() const {return n;} double get_Ort() const {return x;} // Destruktor der Klasse ~Ding(){ printf("Destruktor, zerstört ein Ding \n"); } }; int main(){ // Hauptfunktion Ding Teilchen_A = Ding(); // Benutzt Konstruktor Ding(), n=0, x=0 Ding Teilchen_B = Ding(1); // Benutzt Konstruktor Ding(n), n=1, x=0 Ding Teilchen_C = Ding(2,9.8); // Benutzt Konstruktor Ding(n,x), n=2, x=9.8 Ding Teilchen_D {3,5.1}; // Benutzt Konstruktor Ding(n,x), n=3, x=5.1, andere Schreibweise der Initialisierung printf("\n"); printf("Das Teilchen A hat die Nummer %i und befindet sich an der Stelle %5.2f \n", Teilchen_A.get_Nummer(), Teilchen_A.get_Ort()); printf("Das Teilchen B hat die Nummer %i und befindet sich an der Stelle %5.2f \n", Teilchen_B.get_Nummer(), Teilchen_B.get_Ort()); printf("Das Teilchen C hat die Nummer %i und befindet sich an der Stelle %5.2f \n", Teilchen_C.get_Nummer(), Teilchen_C.get_Ort()); printf("Das Teilchen D hat die Nummer %i und befindet sich an der Stelle %5.2f \n", Teilchen_D.get_Nummer(), Teilchen_D.get_Ort()); printf("\n"); }
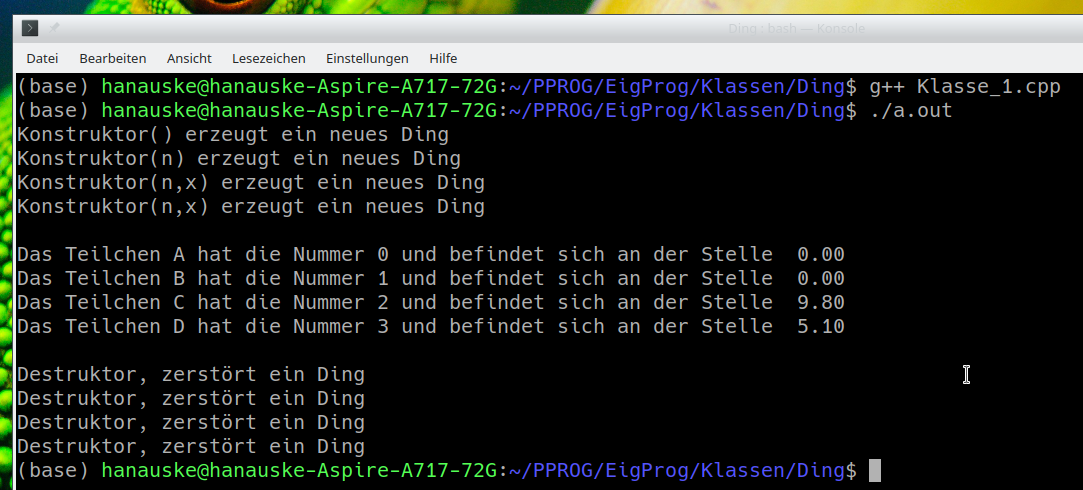
Im Hauptprogramm werden diese Konstruktoren dann benutzt, um vier verschiedene Dinge mit den Namen 'Teilchen_A', 'Teilchen_B', 'Teilchen_C' und 'Teilchen_D' zu erstellen. Es werden hierbei unterschiedliche Formulierungen des Konstruktoraufrufs benutzt (z.B. Ding Teilchen_C = Ding(2,9.8); vs. Ding Teilchen_D {3,5.1}; ), wobei die letztere Variante wohl die zu Präferierende darstellt, da sie den Initialisierungscharakter des Konstruktor Aufrufs am besten gerecht wird.
Obwohl die Instanzvariablen $n$ und $x$ private Größen repräsentieren, kann man mittels öffentlicher Member-Funktionen auch auf die Werte dieser Member-Daten zugreifen. Solche Klasseninterne Funktionen sollten stets mit dem Zusatz const vor dem Anweisungsblock gekennzeichnet sein (hier z.B. double get_Ort() const {return x;}). Am Ende des Hauptprogramms werden diese Member-Funktionen dann mittels des Punktoperators aufgerufen, um die Nummer und den Ort des Objektes im Terminal auszugeben (siehe nebenstehende Abbildung). Bei der Beendigung des Programms werden die Destruktoren für alle vier erzeugten Teilchen aufgerufen.
Die Klasse der Lagrange Polynom Methode
Die Frage, ob es sinnvoll ist ein Programm in eine Klassenstruktur zu bringen ist nicht leicht zu beantworten. Es ist hierbei wichtig, das gesamte Programm auf wiederverwertbare Algorithmen und kapselbare Konzepte zu untersuchen und diese zusammenhängenden Code-Fragmente in einer Klasse sinnvoll und möglichst benutzerfreundlich zu implementieren. Wir hatten in der Vorlesung 5, im Unterpunkt Anwendungsbeispiel: Interpolation und Polynomapproximation die Methode der Lagrange Polynome kennengelernt und diese in einem C++ Programm implementiert (siehe auch Übungsblatt Nr.5, Aufgabe 1). Das Konzept der Lagrange Polynome stellt ein kapselbares, inhaltlich zusammenhängendes Konzept im Programm dar und wir wollen deshalb eine Klasse konstruieren, die der Benutzer anwenden kann, um den Polynomwert an der Stelle $x$ bei einem vorgegebenen Stützstellenarray zu erhalten. Der unten abgebildete C++ Quelltext stellt eine Implementierung einer solchen Klasse dar.
/* Entwicklung einer Funktion in ein Lagrange Polynom (mit ausgelagerter 'LagrangePoly'-Klasse) * Mittels der Methode der Lagrange Polynome entwickelt man eine Funktion ( hier speziell f(x)=1/x ) * durch Angabe von N+1 vorgegebener Punkte in ein Lagrange Polynom vom Grade N. * Hier speziell 7 Punkte * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Lagrange_Polynom_Klasse.dat" */ #include <iostream> // Ein- und Ausgabebibliothek //Definition der Klasse 'LagrangePoly' class LagrangePoly { // Private Instanzvariablen (Daten-Member) der Klasse double* points; // Zeigervariable der Stuetzstellenpunkte unsigned int N_points; // Anzahl der Stuetzstellenpunkte // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Konstruktor mit zwei Argumenten LagrangePoly(double* set_points, unsigned int set_N_points) : points{set_points}, N_points{set_N_points} {} double rechne(double x) { // Member-Funktionen der Klasse zur Berechnung des approximierten Polynomwertes double Pfp = 0; // Deklaration und Initialisierung des Funktionswertes des approximierten Polynoms double Lk = 0; // Deklaration und Initialisierungeiner Zusatzvariable for(int k = 0; k < N_points; ++k){ // For-Schleife der Summation in der Lagrange Polynom Methode Lk=1; // Initialisierung der Produktvariable Lk mit 1 for(int i = 0; i < N_points; ++i){ // For-Schleife der Produktbildung in der Lagrange Polynom Methode if(i != k){ // Die Produktbildung soll nur fuer (i ungleich k) erfolgen Lk = Lk * (x - points[i])/(points[k] - points[i]); // Berechnung der Lk-Werte in der Lagrange Polynom Methode } // Ende if-Bedingung } // Ende for-Schleife der Produktbildung Pfp = Pfp + f(points[k])*Lk; // Kern-Gleichung in der Lagrange Polynom Methode } // Ende for-Schleife der Summenbildung return Pfp; // Rueckgabe des berechneten, approximierten Polynomwertes } // Ende der Member-Funktion rechne(double x) double f(double x){ // Deklaration und Definition der Funktion f(x) die approximiert werden soll double wert; wert = 1.0/x; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) }; // Ende der Klassendefinition int main(){ // Hauptfunktion double points[] = { 1, 1.5, 2, 2.5, 3, 5, 7 }; // Deklaration und Initialisierung der Punkte als double-Datenfeld (Array) unsigned int N_points = sizeof(points)/sizeof(points[0]); // Anzahl der Punkte die zur Approximation verwendet werden double plot_a = 0.5; // Untergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen double plot_b = 6; // Obergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen const unsigned int N_xp=300; // Anzahl der Punkte in die das x-Intervall aufgeteilt wird double dx = (plot_b - plot_a)/N_xp; // Abstand dx zwischen den aequidistanten Punkten des x-Intervalls double x = plot_a-dx; // Aktueller x-Wert double xp[N_xp+1]; // Deklaration der x-Ausgabe-Punkte als double-Array double fp[N_xp+1]; // Deklaration der f(x)-Ausgabe-Punkte als double-Array double Pfp[N_xp+1]; // Deklaration der Ausgabe-Punkte des approximierten Polynoms als double-Array LagrangePoly Poly1 {points,N_points}; // Aufruf des Konstruktors der Klasse LagrangePoly (Erzeugung des Objektes 'Poly1') printf("# x-Werte der %3d Stuetzstellen-Punkte: \n", N_points); // Beschreibung der ausgegebenen Groessen for(int k = 0; k < N_points; ++k){ // For-Schleife der Ausgabe der Stuetzstellen x-Werte printf("%10.5f",points[k]); // Ausgabe der Stuetzpunkte } // Ende for-Schleife der Ausgabe printf("\n"); // Zeilenumbruch printf("# 0: Index j \n# 1: x-Wert \n# 2: f(x)-Wert \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Approximierter Wert des Lagrange Polynoms P(x) \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Fehler zum wirklichen Wert f(x)-P(x) \n"); // Beschreibung der ausgegebenen Groessen for(int j = 0; j <= N_xp; ++j){ // For-Schleife die ueber die einzelnen Punkte des x-Intervalls geht x = x + dx; // Aktueller x-Wert xp[j] = x; // Eintrag des aktuellen x-Wertes in das x-Array fp[j] = Poly1.f(x); // Eintrag des aktuellen f(x)-Wertes in das fp-Array (Aufruf der Member-Funktion f(x)) Pfp[j] = Poly1.rechne(x); // Eintrag des aktuellen approximierten Polynom-Wertes in das Pfp-Array (Aufruf der Member-Funktion rechne(x)) } // Ende der for-Schleife ueber die einzelnen Punkte des x-Intervalls for(int j = 0; j <= N_xp; ++j){ // For-Schleife der separaten Ausgabe der berechneten Werte printf("%3d %14.10f %14.10f %14.10f %14.10f \n",j, xp[j], fp[j], Pfp[j], (fp[j] - Pfp[j])); // Ausgabe der berechneten Werte } // Ende for-Schleife der Ausgabe } // Ende der Hauptfunktion
Man hätte die zugrundeliegende Funktion auch außerhalb der Klasse definieren können, wobei man dann die Funktion innerhalb der Klasse zunächst deklariert und bei der Definition der Funktion den Zusatz 'inline' verwendet: inline double LagrangePoly::f(double x){ ... } (siehe folgendes Programm).
/* Entwicklung einer Funktion in ein Lagrange Polynom (mit ausgelagerter 'LagrangePoly'-Klasse und inline-Member Funktion f(x)) * Mittels der Methode der Lagrange Polynome entwickelt man eine Funktion ( hier speziell f(x)=1/x ) * durch Angabe von N+1 vorgegebener Punkte in ein Lagrange Polynom vom Grade N. * Hier speziell 7 Punkte * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Lagrange_Polynom_Klassea.dat" */ #include <iostream> // Ein- und Ausgabebibliothek //Definition der Klasse 'LagrangePoly' class LagrangePoly { // Private Instanzvariablen (Daten-Member) der Klasse double* points; // Zeigervariable der Stuetzstellenpunkte unsigned int N_points; // Anzahl der Stuetzstellenpunkte // Oeffentliche Konstruktoren und Member-Funktionen der Klasse public: // Konstruktor mit zwei Argumenten LagrangePoly(double* set_points, unsigned int set_N_points) : points{set_points}, N_points{set_N_points} {} double f(double x); // Deklaration der Member-Funktion f(x) (Definition findet ausserhalb der Klasse statt) double rechne(double x) { // Member-Funktion der Klasse zur Berechnung des approximierten Polynomwertes double Pfp = 0; // Deklaration und Initialisierung des Funktionswertes des approximierten Polynoms double Lk = 0; // Deklaration und Initialisierungeiner Zusatzvariable for(int k = 0; k < N_points; ++k){ // For-Schleife der Summation in der Lagrange Polynom Methode Lk=1; // Initialisierung der Produktvariable Lk mit 1 for(int i = 0; i < N_points; ++i){ // For-Schleife der Produktbildung in der Lagrange Polynom Methode if(i != k){ // Die Produktbildung soll nur fuer (i ungleich k) erfolgen Lk = Lk * (x - points[i])/(points[k] - points[i]); // Berechnung der Lk-Werte in der Lagrange Polynom Methode } // Ende if-Bedingung } // Ende for-Schleife der Produktbildung Pfp = Pfp + f(points[k])*Lk; // Kern-Gleichung in der Lagrange Polynom Methode } // Ende for-Schleife der Summenbildung return Pfp; // Rueckgabe des berechneten, approximierten Polynomwertes } // Ende der Member-Funktion rechne(double x) }; // Ende der Klassendefinition inline double LagrangePoly::f(double x){ // Definition der Funktion f(x) als inline-Methode der Klasse LagrangePoly double wert; wert = 1.0/x; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) int main(){ // Hauptfunktion double points[] = { 1, 1.5, 2, 2.5, 3, 5, 7 }; // Deklaration und Initialisierung der Punkte als double-Datenfeld (Array) unsigned int N_points = sizeof(points)/sizeof(points[0]); // Anzahl der Punkte die zur Approximation verwendet werden double plot_a = 0.5; // Untergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen double plot_b = 6; // Obergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen const unsigned int N_xp = 300; // Anzahl der Punkte in die das x-Intervall aufgeteilt wird double dx = (plot_b - plot_a)/N_xp; // Abstand dx zwischen den aequidistanten Punkten des x-Intervalls double x = plot_a-dx; // Aktueller x-Wert double xp[N_xp+1]; // Deklaration der x-Ausgabe-Punkte als double-Array double fp[N_xp+1]; // Deklaration der f(x)-Ausgabe-Punkte als double-Array double Pfp[N_xp+1]; // Deklaration der Ausgabe-Punkte des approximierten Polynoms als double-Array LagrangePoly Poly1 {points,N_points}; // Aufruf des Konstruktors der Klasse LagrangePoly (Erzeugung des Objektes 'Poly1') printf("# x-Werte der %3d Stuetzstellen-Punkte: \n", N_points); // Beschreibung der ausgegebenen Groessen for(int k = 0; k < N_points; ++k){ // For-Schleife der Ausgabe der Stuetzstellen x-Werte printf("%10.5f",points[k]); // Ausgabe der Stuetzpunkte } // Ende for-Schleife der Ausgabe printf("\n"); // Zeilenumbruch printf("# 0: Index j \n# 1: x-Wert \n# 2: f(x)-Wert \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Approximierter Wert des Lagrange Polynoms P(x) \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Fehler zum wirklichen Wert f(x)-P(x) \n"); // Beschreibung der ausgegebenen Groessen for(int j = 0; j <= N_xp; ++j){ // For-Schleife die ueber die einzelnen Punkte des x-Intervalls geht x = x + dx; // Aktueller x-Wert xp[j] = x; // Eintrag des aktuellen x-Wertes in das x-Array fp[j] = Poly1.f(x); // Eintrag des aktuellen f(x)-Wertes in das fp-Array (Aufruf der Member-Funktion f(x)) Pfp[j] = Poly1.rechne(x); // Eintrag des aktuellen approximierten Polynom-Wertes in das Pfp-Array (Aufruf der Member-Funktion rechne(x)) } // Ende der for-Schleife ueber die einzelnen Punkte des x-Intervalls for(int j = 0; j <= N_xp; ++j){ // For-Schleife der separaten Ausgabe der berechneten Werte printf("%3d %14.10f %14.10f %14.10f %14.10f \n",j, xp[j], fp[j], Pfp[j], (fp[j] - Pfp[j])); // Ausgabe der berechneten Werte } // Ende for-Schleife der Ausgabe } // Ende der Hauptfunktion