Anwendungsbeispiel: Interpolation und Polynomapproximation
Die Interpolation ist ein Teilgebiet der numerischen Mathematik und es befasst sich mit der Problematik, eine analytische Funktion mittels einer gegebenen Menge von Werten zu bestimmen. Wir werden in diesem Unterpunkt den wohl elementarsten Algorithmus einer Interpolation vorstellen, bei dem ein Polynom $P(x)$ mittels einer gegebenen Liste von Werten konstruiert wird. Aufgrund des Weierstraßschen Approximationssatzes gibt es für jede, auf einem Teilintervall $[a,b]$ definierte, stetige Funktion, $f(x)$ ein Polynom $P(x)$ mit der Eigenschaft, dass für jedes $\epsilon > 0$ die Differenz der Funktion mit dem Polynom verschwindend klein wird ($\left| f(x) - P(x) \right| < \epsilon \,\, \forall \, x \in [a,b]$). Die Taylorschen Polynome sind hierbei wohl das bekannteste Beispiel einer Entwicklung einer Funktion in ein Polynom. Leider haben die Taylorschen Polynome den Nachteil, dass sie von ihrer Konstruktion her nur eine Stützstelle $x_0 \in [a,b]$ verwenden und somit die Funktion $f(x)$ zwar gut in dem Bereich um die Stützstelle beschreiben, aber nicht im gesamten Teilintervall $[a,b]$. Bei einer Interpolation mittels der Methode der Lagrange Polynome verwendet man hingegen mehrere Stützstellenpunkte für die Konstruktion des approximierenden Polynoms. Dieses Verfahren ist Gegenstand dieses Anwendungsbeispiels.
Die Theorie der Entwicklung einer Funktion in ein Lagrange Polynom
Bei der Entwicklung einer Funktion in ein Lagrange Polynom steht man vor der Aufgabe eine Funktion $f(x)$ mittels ($n+1$) vorgegebener Punkte ($(x_0,f(x_0)), (x_1,f(x_1)), ..., (x_n,f(x_n))$) in ein Lagrange Polynom vom Grade $n$ zu entwickeln. Das n-te Lagrange Polynom $P_n(x)$ einer Funktion $f(x)$ ist wie folgt definiert: \[ \begin{equation} P_n(x) = \sum_{k=0}^n f(x_k) \cdot L_{n,k}(x) \quad, \, \hbox{wobei} \quad L_{n,k}(x) = \prod_{i=0 , \, i \neq k}^n \frac{(x-x_i)}{(x_k-x_i)} \quad. \end{equation} \] Approximiert man z.B. die Funktion $f(x)=\frac{1}{x}$ im Teilintervall $[a,b]=[0.5,6]$ mittels dreier vorgegebener Punkte ($n=2$, mit $n+1$ Punkten $(2,f(2)), (2.5,f(2.5))$ und $(4,f(4)) $) in ein Lagrange Polynom vom Grade 2, so erhält man: \[ \begin{eqnarray} P_2(x) = \sum_{k=0}^2 f(x_k) \cdot L_{2,k}(x) &=& f(x_0) \cdot L_{2,0}(x) + f(x_1) \cdot L_{2,1}(x) + f(x_2) \cdot L_{2,2}(x) \\ &=& \frac{1}{2} \cdot L_{2,0}(x) + \frac{1}{2.5} \cdot L_{2,1}(x) + \frac{1}{4} \cdot L_{2,2}(x) \\ \hbox{mit:} && L_{2,0}(x) = \prod_{i=0 , \, i \neq 0}^2 \frac{(x-x_i)}{(x_0-x_i)} = \frac{(x-x_1)}{(x_0-x_1)} \cdot \frac{(x-x_2)}{(x_0-x_2)} = \frac{(x-2.5)}{(2-2.5)} \cdot \frac{(x-4)}{(2-4)} = \frac{(x-2.5)}{(-0.5)} \cdot \frac{(x-4)}{(-2)} \\ && L_{2,1}(x) = \prod_{i=0 , \, i \neq 1}^2 \frac{(x-x_i)}{(x_1-x_i)} = \frac{(x-x_0)}{(x_1-x_0)} \cdot \frac{(x-x_2)}{(x_1-x_2)} = \, ... \\ && L_{2,2}(x) = \prod_{i=0 , \, i \neq 2}^2 \frac{(x-x_i)}{(x_2-x_i)} = \frac{(x-x_0)}{(x_2-x_0)} \cdot \frac{(x-x_1)}{(x_2-x_1)} = \, ... \\ \Longrightarrow P_2(x) = 0.05 \, x^2 - 0.425 \, x + 1.15 && \end{eqnarray} \]
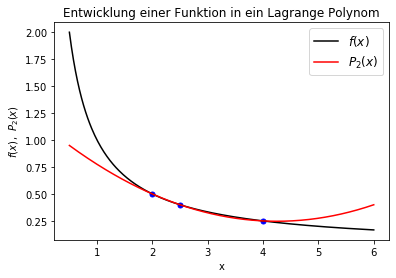
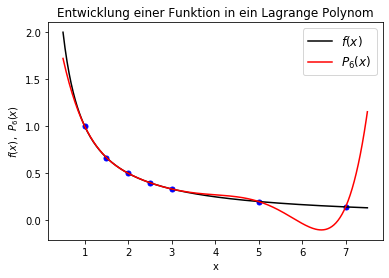
Die nebenstehende linke Abbildung verdeutlicht die oben beschriebene Lagrange Polynom Entwicklung, wobei die blauen Punkte die drei vorgegebenen Stützstellen des Polynoms darstellen, bei welchen die Übereinstimmung $f(x_k)=P_2(x_k)$ exakt gilt. Die rechte Abbildung zeigt das entsprechende Polynom $P_6(x)$, wobei hier die sieben Stützstellen an den folgenden x-Werten genommen wurden: $\vec{x}=\left( 1, 1.5, 2, 2.5, 3, 5, 7 \right)$.
Im Folgenden werden wir den beschriebenen Algorithmus der Entwicklung einer Funktion in ein Lagrange Polynom, mittels eines C++ Programms durchführen. In Abhängigkeit von der Anzahl der eingegebenen Stützstellen ($n+1$) soll das n-te Lagrangesche Polynom $P_n(x)$ bestimmt werden. Hierbei werden wir die Liste der Stützstellen $\vec{x}=\left( x_0, x_1, \, ... \,, x_n \right)$ als ein eindimensionales C++ Array deklarieren und ebenso die Liste der Funktionswerte des berechneten Polynoms $P_n(x)$ in einem eindimensionalen C++ Array speichern.
Die Abbildungen zeigen, dass die Übereinstimmung des berechneten Polynoms $P_n(x)$ mit der Funktion $f(x)$ nur an den Stützstellen exakt ist. Betrachtet man sich den Unterschied beider Funktionen an einem beliebigen x-Wert im Bereich der Stützstellen, so kann man die folgende Fehlerformel des Lagrangeschen Polynoms herleiten \[ \begin{equation} f(x) = P_n(x) + \underbrace{ \frac{f^{(n+1)}(\xi(x))}{(n+1)!} \prod_{i=0}^n (x-x_i) }_{\hbox{Fehler}} \,\, , \,\, \forall \,\, \xi(x) \in [x_0,x_n] \quad, \end{equation} \] wobei $f^{(n+1)(x)}$ die $(n+1)$-te Ableitung der Funktion darstellt und $\xi(x)$ ein x-Wert im Bereich der Stützstellen ist.
Das C++ Programm
Das folgende C++ Programm (Lagrange_Polynom_1.cpp) stellt eine Implementierung der Lagrange Polynom Methode dar:
/* Entwicklung einer Funktion in ein Lagrange Polynom * Mittels der Methode der Lagrange Polynome entwickelt man eine Funktion ( hier speziell f(x)=1/x ) * durch Angabe von n+1 vorgegebener Punkte in ein Lagrange Polynom vom Grade n. * Hier speziell 3 Punkte ( (2,f(2)), (2.5,f(2.5)), (4,f(4)) ) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out >> Lagrange_Polynom_1.dat" */ #include <iostream> // Ein- und Ausgabebibliothek double f(double x){ // Deklaration und Definition der Funktion f(x) die approximiert werden soll double wert; wert = 1.0/x; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) int main(){ // Hauptfunktion double points[] = { 2, 2.5, 4 }; // Deklaration und Initialisierung der Stützstellen als double-Array const unsigned int N_points = sizeof(points)/sizeof(points[0]); // Anzahl der Punkte die zur Approximation verwendet werden double a = 0.5; // Untergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen double b = 6; // Obergrenze des x-Intervalls in dem die Ergebnisse ausgegeben werden sollen const unsigned int N_xp=300; // Anzahl der Punkte in die das x-Intervall aufgeteilt wird double dx = (b - a)/N_xp; // Abstand dx zwischen den aequidistanten Punkten des x-Intervalls double x; // Deklaration des aktuellen x-Wertes double xp[N_xp+1]; // Deklaration der x-Ausgabe-Punkte als double-Array double fp[N_xp+1]; // Deklaration der f(x)-Ausgabe-Punkte als double-Array double Pfp[N_xp+1]; // Deklaration der Ausgabe-Punkte des approximierten Polynoms als double-Array double Lk; // Deklaration einer Variable, die fuer Zwischenrechnungen benoetigt wird printf("# x-Werte der %3d Stuetzstellen-Punkte: \n", N_points); // Beschreibung der ausgegebenen Groessen for(int k = 0; k < N_points; ++k){ // For-Schleife der Ausgabe der Stuetzstellen x-Werte printf("%10.5f",points[k]); // Ausgabe der Stuetzpunkte } // Ende for-Schleife der Ausgabe printf("\n"); // Zeilenumbruch printf("# 0: Index j \n# 1: x-Wert \n# 2: f(x)-Wert \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Approximierter Wert des Lagrange Polynoms P(x) \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Fehler zum wirklichen Wert f(x)-P(x) \n"); // Beschreibung der ausgegebenen Groessen for(int j = 0; j <= N_xp; ++j){ // For-Schleife die ueber die einzelnen Punkte des x-Intervalls geht x = a + j*dx; // Aktueller x-Wert xp[j]=x; // Eintrag des aktuellen x-Wertes in das x-Array fp[j]=f(x); // Eintrag des aktuellen f(x)-Wertes in das f(x)-Array Pfp[j]=0; // Initialisierung des j-ten Polynom-Arrays mit 0 (Wert beim Anfang der Summenbildung) for(int k = 0; k < N_points; ++k){ // For-Schleife der Summation in der Lagrange Polynom Methode Lk=1; // Initialisierung der Produktvariable Lk mit 1 for(int i = 0; i < N_points; ++i){ // For-Schleife der Produktbildung in der Lagrange Polynom Methode if(i != k){ // Die Produktbildung soll nur fuer (i ungleich k) erfolgen Lk = Lk * (x - points[i])/(points[k] - points[i]); // Berechnung der Lk-Werte in der Lagrange Polynom Methode } // Ende if-Bedingung } // Ende for-Schleife der Produktbildung Pfp[j] = Pfp[j] + f(points[k])*Lk; // Kern-Gleichung in der Lagrange Polynom Methode } // Ende for-Schleife der Summenbildung } // Ende der for-Schleife ueber die einzelnen Punkte des x-Intervalls for(int j = 0; j <= N_xp; ++j){ // For-Schleife der separaten Ausgabe der berechneten Werte printf("%3d %14.10f %14.10f %14.10f %14.10f \n",j, xp[j], fp[j], Pfp[j], (fp[j] - Pfp[j])); // Ausgabe der berechneten Werte } // Ende for-Schleife der Ausgabe } // Ende der Hauptfunktion
Das C++ Programm verwendet eine Funktionendefinition (siehe Unterpunkt Funktionen in C++), um die zu approximierende Funktion $f(x)$ im Programm zu implementieren. In der main()-Funktion wird zunächst der Vektor $\vec{x}=\left( 2, 2.5, 4 \right)$ der x-Werte der Stützstellenpunkte als ein double-Array "double points[]" deklariert und direkt mit den Stützstellenwerten initialisiert. Die Dimension dieses eindimensionalen Arrays (Anzahl der Stützstellenpunkte) wird danach ermittelt und als "const unsigned int N_points" gespeichert. Mittels dieser Implementierung ist eine Veränderung der Stützstellen einfach möglich und möchte man z.B. mehrere Stützstellen verwenden, kann man die weiteren Stützstellen einfach dem Initialisierungsvektor hinzufügen. Das C++ Programm soll nun, in Abhängigkeit von dem gewählten Vektor $\vec{x}$ mit ($n+1$)-Stützstellen, das n-te Lagrange-Polynom $P_n$ berechnen, wobei der Grad $n$ des Polynoms gerade um Eins kleiner als die Dimension des Arrays "points[]" ist (n = N_points-1).
Das zu berechnende Polynom kann in einem numerischen C++ Programm nicht als eine analytische Gleichung ausgegeben werden, sondern wir möchten vielmehr eine xy-Wertetabelle des Polynoms $P_n(x)$ im betrachteten Teilintervall $x \in [a,b]$ ausgeben lassen, um sie dann mit der Funktion $f(x)$ vergleichen zu können. Im folgenden Verlauf des oben abgebildeten C++ Quelltextes wird das Teilintervall $[a,b]$ und die Anzahl der Punkte der Ausgabe definiert. Die berechneten xy-Werte des Polynoms $P_n(x)$ und der Funktion $f(x)$ sollen in Datenarrays gespeichert werden und diese dann formatiert ausgegeben werden. Hierzu deklarieren wir drei zusätzliche double-Arrays (xp[N_xp+1], fp[N_xp+1] und Pfp[N_xp+1]) mit denen wir die x-Werte, die $f(x)$-Werte und die $P_n(x)$-Werte speichern. Nun beginnt die erste Terminalausgabe, wobei zunächst der benutzte Stützstellenvektor ausgegeben wird und danach die Beschreibung der auszugegebenen Zahlentabelle folgt. Es werden der Index j des Plotpunktes, der x-Wert, der $f(x)$-Wert, der approximierte Wert des Lagrange Polynoms $P_n(x)$ und der Fehler zum wirklichen Wert $f(x)-P_n(x)$ ausgegeben. Die jetzt folgende for-Schleife geht über die einzelnen Punkte des x-Intervalls $[a,b]$ in äquidistanten Schritten von dx.
Der nun folgende Teil des Programms ist der eigentliche Berechnungsteil der Lagrange Polynom Methode. Mittels zweier geschachtelter for-Schleifen wird die Summen- und Produktbildung im Programm implementiert und für den aktuellen x-Wert, der entsprechende y-Wert des Polynoms $P_n(x)$ berechnet. Die letzte for-Schleife gibt schließlich die berechneten Werte im Terminal aus.
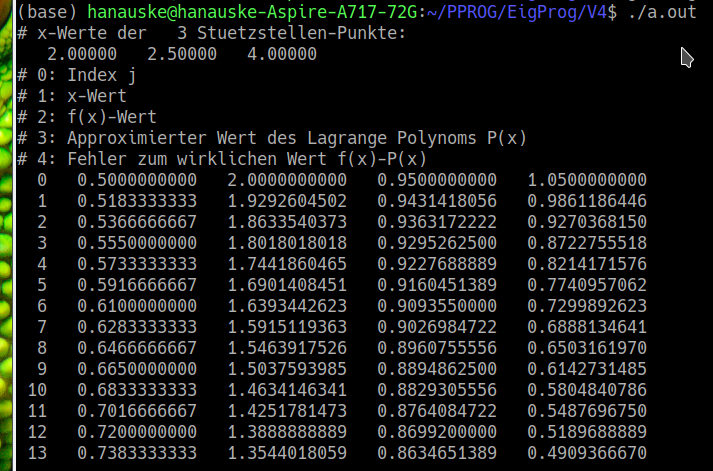
Die oberen Abbildungen zeigen die Terminalausgabe des Programms. Im nächsten Unterkapitel werden die berechneten Daten mittels eines Jupyter Notebooks visualisiert. Hierzu wurde die Terminalausgabe mittels des Befehls "./a.out > Lagrange_Polynom_1.dat" in eine Textdatei umgeleitet und zusätzlich eine weitere Berechnung eines Lagrange Polynoms vom Grade $n=6$ ($P_6(x)$) im Teilintervall $[a,b]=[0.5,7.5]$ mit sieben Stützstellen ($\vec{x}=\left( 1, 1.5, 2, 2.5, 3, 5, 7 \right)$) durchgeführt und in die Datei "Lagrange_Polynom_2.dat" umgeleitet.
Der im C++ Programm implementierte Algorithmus stellt eine nützliche Berechnung dar, die man vielleicht auch in anderen Programmen verwenden kann. Es wäre deshalb von Vorteil, wenn man den Kern-Algorithmus des Programms in eine Funktion auslagern könnte (siehe Aufgabe 1 im Übungsblatt Nr.5).
Visualisierung mittels eines Jupyter Notebooks
Wir möchten uns nun die berechneten numerischen Werte der Lagrangepolynome $P_2(x)$ und $P_6(x)$ visualisieren und diese mit ihrer Urfunktion $f(x)$ vergleichen. Dies wird im nebenstehenden Jupyter Notebook gemacht. Zusätzlich wird in diesem Notebook auch die analytische Form der Polynome unter Verwendung der Computer-Algebra-Bibliothek "sympy" berechnet. Mittels des Python Modul "sympy" sind eine Vielzahl von symbolischen Berechnungen im Bereich der Mathematik und Physik relativ einfach möglich (die 'sympy'-Bibliothek` werden wir in der nächsten Vorlesung genauer vorstellen). Beim Klicken auf das nebenstehende Bild gelangen Sie zu dem html-Export des Notebooks LagrangePolynome.ipynb.