Mehrdimensionale C++ Arrays
Dieser Unterpunkt baut auf dem Thema C++ Arrays, Zeiger und Referenzen der vorigen Vorlesung auf und betrachtet mehrdimensionale C++ Arrays. Mehrdimensionale C++ Arrays werden im Prinzip als ein Array von Arrays dargestellt und sie beschreiben einen Matrix-ähnlichen integrierten Datentyp. Für einen Typ T entspricht "T Name[m][n];" der Deklaration einer $(m \times n)$-Matrix, wobei die einzelnen Elemente vom gleichen Typ T sein müssen. Möchten wir z.B. eine $(m \times n)$-Matrix ${\bf \cal A}$, bestehend aus Gleitkommazahlen vom Typ double in einem C++ Programm als ein integriertes Array deklarieren, so würden wir die folgende Anweisung in den Quelltext schreiben: double A[m][n]; \[ \begin{equation} {\bf \cal A} =\left( \begin{array}{cccc} a_{11} & a_{12} & ... & a_{1n}\\ a_{21}& a_{22}& ...&a_{2n} \\ ...& ...& ...& ...\\ a_{m1}& a_{m2}& ...& a_{mn}\\ \end{array} \right) = (a_{ij})_{i=1,2,...,m \, ; \, j=1,2,...,n} \quad \Longrightarrow \quad \hbox{Deklaration z.B. mit: double A[m][n];} \end{equation} \] Im Folgenden werden wir zunächst auf den Zusammenhang von mehrdimensionalen C++ Arrays mit Zeigern eingehen.
Mehrdimensionale C++ Arrays und Zeiger
In gleicher Weise wie auch bei eindimensionalen Arrays sind mehrdimensionale C++ Arrays mittels des Konstruktes des Zeigers implementiert. Die einzelnen Elemente eines Arrays (z.B. "double A[m][n]") sind in Form von Zeigern auf die eindimensionalen Zeilen-Unterarrays geordnet. Der Zugriff auf den Wert eines Array-Elementes kann entweder durch die Angabe des entsprechenden Matrix-Indexes (A[i][j]), oder durch den dereferenzierten Wert seiner Zeigerposition im Array erfolgen ( *(A[i] + j) bzw. *(zeiger_A + i*n + j) ). Dies Eigenschaften von mehrdimensionale C++ Arrays wollen wir nun am Beispiel von int-Arrays näher betrachten.
In dem folgenden C++ Programm werden zwei int-Arrays definiert, die den folgenden zwei Matrizen ${\bf \cal A}$ und ${\bf \cal B}$ entsprechen: \[ \begin{equation} \hbox{$(3 \times 5)$-Matrix} \quad {\bf \cal A} =\left( \begin{array}{ccccc} 1 & 2 & 3 & 4& 5\\ 21 & 22 & 23 & 24 & 25 \\ 51 & 52 & 53 & 54 & 55\\ \end{array} \right) \quad , \qquad \hbox{$(5 \times 3)$-Matrix} \quad {\bf \cal B} =\left( \begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \\ 13 & 14 & 15 \\ \end{array} \right) \end{equation} \]
/** Definition von integrierten mehrdimensionalen C++ Arrays * (m x n)-Matrix: Eine Matrix mit m Zeilen und n Spalten * hier speziell eine (3 x 5)-Matrix A und eine (5 x 3)-Matrix B **/ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion const int m = 3; const int n = 5; int A[m][n] = { { 1, 2, 3, 4, 5}, {21,22,23,24,25}, {51,52,53,54,55} }; // Definition eines (3x5)-Integer-Arrays ((3x5)-Matrix) int B[n][m] = { { 1, 2, 3}, { 4, 5, 6}, { 7, 8, 9}, {10,11,12}, {13,14,15} }; // Definition eines (5x3)-Integer-Arrays ((5x3)-Matrix) int* zeiger_A = &A[0][0]; // Definition des Zeigers auf das Integer-Array A constexpr int anz_elem_A = sizeof(A)/sizeof(A[0][0]); // Gesamte Anzahl der Elemente im Array A constexpr int dim_m = sizeof(A)/sizeof(A[0]); // Dimension m des Arrays (Anzahl der Zeilen der Matrix A) constexpr int dim_n = sizeof(A[0])/sizeof(A[0][0]); // Dimension n des Arrays (Anzahl der Spalten der Matrix A) printf("Matrix A: \n"); for(int i=0; i < m; ++i){ // Anfang Schleife 1 (Zeilen der Matrix) printf("| "); for(int j=0; j < n; ++j){ // Anfang Schleife 2 (Spalten der Matrix) printf("%3i ", A[i][j]); // Ausgabe des Matrixwertes A_{ij} } // Ende der 2.Schleife printf("| \n"); } // Ende der 1.Schleife printf("\nMatrix B: \n"); for(int i=0; i < n; ++i){ // Anfang Schleife 1 (Zeilen der Matrix) printf("| "); for(int j=0; j < m; ++j){ // Anfang Schleife 2 (Spalten der Matrix) printf("%3i ", B[i][j]); // Ausgabe des Matrixwertes B_{ij} } // Ende der 2.Schleife printf("| \n"); } // Ende der 1.Schleife printf("\nDie Adresse des mehrdimensionalen Arrays A entspricht der Referenz seines ersten Elementes:\n"); printf("&A[0][0] = %p , A[0] = %p und zeiger_A = %p\n\n", &A[0][0], A[0], zeiger_A); printf("Der Ausdruck A[i] ist der Zeiger auf die i-te Zeile der Matrix A:\nA[0] = %p , A[1] = %p und A[2] = %p \n\n", A[0], A[1], A[2]); printf("Die gesamte Anzahl der Elemente im Array A ist %i \n\n", anz_elem_A); printf("Das Array A entspricht einer (m x n)-Matrix mit m = %i und n = %i \n\n", dim_m, dim_n); printf("Navigieren in Arrays:\n"); printf("Der Zugriff auf ein Element des Arrays kann entweder ... \n"); printf("... durch die Angabe des Matrix-Indexes erfolgen A[i][j]: z.B. A[2][3] = %i \n", A[2][3]); printf("... oder durch den dereferenzierten Wert seiner Zeigerposition im Array erfolgen *(A[i] + j): z.B. *(A[2] + 3) = %i \n", *(A[2] + 3)); printf(" dies ist gleichbedeutend mit *(zeiger_A + i*n + j): z.B. *(zeiger_A + 2*5 + 3) = %i \n\n", *(zeiger_A + 2*5 + 3)); }
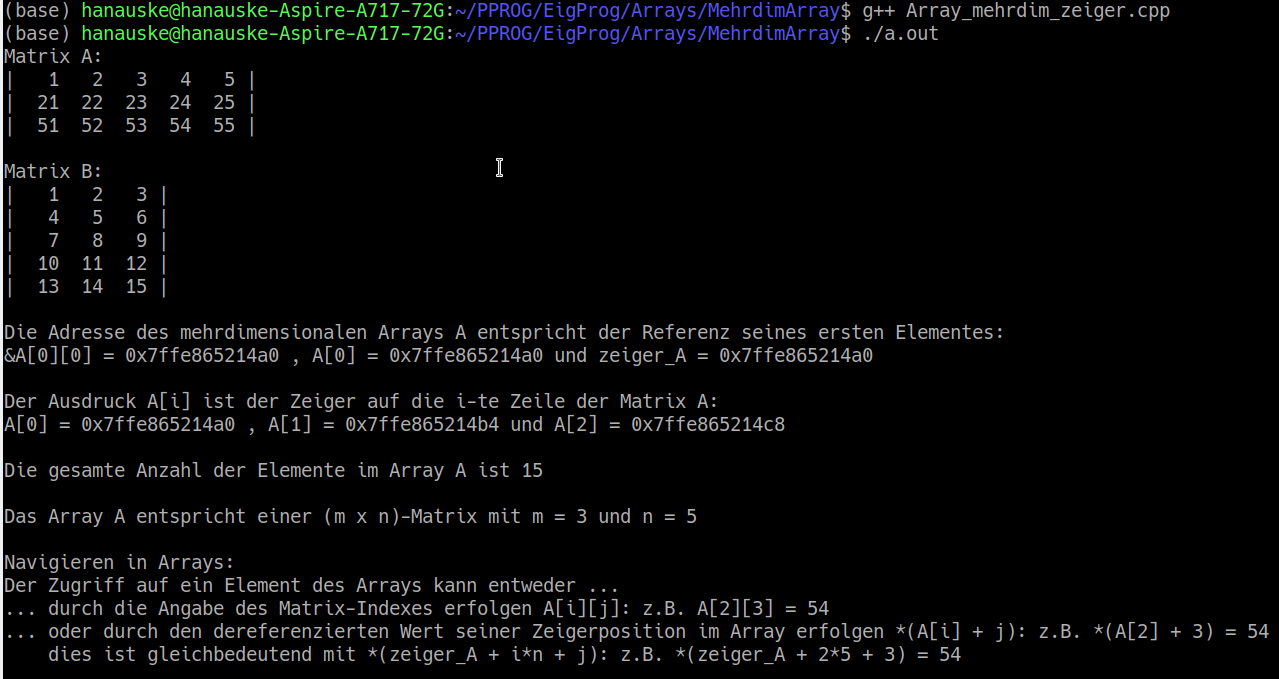
Die Werte der Arrays werden direkt bei ihrer Deklaration initialisiert. Zusätzlich wird der Zeiger auf das Array "A" mittels der Referenz seines ersten Elementes definiert (int* zeiger_A = &A[0][0];). Ähnlich wie bei eindimensionalen Arrays kann man mittels des sizeof(...) Befehls die gesamte Anzahl der Elemente im Array und die Dimensionen des Arrays bestimmen. Mittels zweier geschachtelter for-Schleifen werden dann die Matrizen im Terminal ausgegeben. Die Ausgabe der einzelnen Matrixwerte wird hierbei mittels der Anweisung "printf("%3i ", A[i][j]);" gemacht. Man hätte die Werte "A[i][j]" auch auf Basis des Zeigerkonstruktes wie folgt formulieren können: *(A[i] + j)); bzw. *(zeiger_A + i*n + j));
Da das Navigieren im Array auf Zeigerbasis zunächst ein wenig unübersichtlich erscheint, werden am Ende des Programms einige Adressen/Referenz- und Zeigereigenschaften von mehrdimensionalen C++ Arrays im Terminal ausgegeben. Die linke Abbildung veranschaulicht die gesamte Terminalausgabe des Programms.
Anwendung: Multiplikation zweier Matrizen
Wir möchten nun die beiden Matrizen ${\bf \cal A}$ und ${\bf \cal B}$ miteinander multiplizieren. Allgemein gilt für die Multiplikation einer $(m \times n)$-Matrix ${\bf \cal A}$ mit einer $(n \times l)$-Matrix ${\bf \cal B}$ die folgende Formel: ${\bf \cal C} = {\bf \cal A} \cdot {\bf \cal B}$ mit \[ \begin{equation} c_{ij} = \sum_{k=1}^n a_{ik} \, b_{kj} \quad \, , \quad i=1,2,...,m \, ; \, j=1,2,...,l \quad , \end{equation} \] wobei die entstehende Produktmatrix ${\bf \cal C}$ eine $(m \times l)$-Matrix ist. Für unsere speziellen Matrizen gilt \[ \begin{equation} {\bf \cal C} = {\bf \cal A} \cdot {\bf \cal B} = \underbrace{ \left( \begin{array}{ccccc} 1 & 2 & 3 & 4& 5\\ 21 & 22 & 23 & 24 & 25 \\ 51 & 52 & 53 & 54 & 55\\ \end{array} \right) }_{\hbox{$(3 \times 5)$-Matrix}} \cdot \underbrace{ \left( \begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \\ 13 & 14 & 15 \\ \end{array} \right) }_{\hbox{$(5 \times 3)$-Matrix}} = \underbrace{ \left( \begin{array}{ccc} 135 & 150 & 165 \\ 835 & 950 & 1065 \\ 1885 & 2150 & 2415\\ \end{array} \right) }_{\hbox{$(3 \times 3)$-Matrix}} \quad . \end{equation} \]
Die Multiplikation der Matrizen ${\bf \cal A}$ und ${\bf \cal B}$ ist in dem folgenden C++ Programm mittels dreier geschachtelter for-Schleifen realisiert worden.
/** Matrix Multiplikation * (m x l)-Matrix = (m x n)-Matrix * (n x l)-Matrix * Spezialfall * (m x m)-Matrix = (m x n)-Matrix * (n x m)-Matrix * C[m][m] = A[m][n] * B[n][m] * hier speziell eine (3 x 5)-Matrix A und eine (5 x 3)-Matrix B **/ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion const int m = 3; // Dimension der Zeilen der Matrix A const int n = 5; // Dimension der Spalten der Matrix A int A[m][n] = { { 1, 2, 3, 4, 5}, {21,22,23,24,25}, {51,52,53,54,55} }; // Definition eines (3x5)-Integer-Arrays, (3x5)-Matrix int B[n][m] = { { 1, 2, 3}, { 4, 5, 6}, { 7, 8, 9}, {10,11,12}, {13,14,15} }; // Definition eines (5x3)-Integer-Arrays, (5x3)-Matrix int C[m][m]; // Deklaration eines (3x3)-Integer-Arrays, (3x3)-Matrix // Matrix Multiplikation C = A * B for(int i=0; i < m; ++i){ // Anfang Schleife 1 (Zeilen der Matrix C) for(int j=0; j < m; ++j){ // Anfang Schleife 2 (Spalten der Matrix C) C[i][j] = 0; // Anfangs-Initialisierung von C_{ij} for(int k=0; k < n; ++k){ // Anfang Schleife 3 (Summationsschleife) C[i][j] = C[i][j] + A[i][k] * B[k][j]; // Matrix Multiplikation } // Ende der 3.Schleife } // Ende der 2.Schleife } // Ende der 1.Schleife // Terminal Ausgabe der Matrix C printf("Die Matrix Multiplikation ergibt C = A * B : \n"); for(int i=0; i < m; ++i){ // Anfang Schleife 1 (Zeilen der Matrix) printf("| "); for(int j=0; j < m; ++j){ // Anfang Schleife 2 (Spalten der Matrix) printf("%3i ", C[i][j]); // Ausgabe des Matrixwertes C_{ij} } // Ende der 2.Schleife printf("| \n"); } // Ende der 1.Schleife }
Die Implementierung der eigentlichen Multiplikation im Quelltext wurde mittels der Index-Schreibweise realisiert, da diese dem mathematischen Formalismus sehr ähnelt:
$
c_{ij} = \sum_{k=1}^n a_{ik} \, b_{kj} \quad \Longleftrightarrow \qquad
$
for(int k=0; k < n; ++k){ C[i][j] = C[i][j] + A[i][k] * B[k][j]; }
Nach der Berechnung der einzelnen Elemente des Arrays wird die Produktmatrix ${\bf \cal C}$ schließlich im Terminal ausgegeben.
Mehrdimensionale C++ Arrays und Funktionen
Wie bei eindimensionalen Arrays (siehe Vorlesung 5, C++ Arrays, Zeiger und Referenzen) können auch mehrdimensionale C++ Arrays mittels der Methoden Call-by-Pointer oder Call-by-Reference übergeben werden und eine Methode Call-by-Value ist bei ihnen ebenfalls nicht zu verwenden, da sie zu Zeigern zerfallen. Im folgenden C++ Programm wurde eine void-Funktion dem Hauptprogramm ausgelagert, die zur Aufgabe hat eine $(m \times n)$-Matrix im Terminal auszugeben und dabei die Methode Call-by-Pointer verwendet. Das mehrdimensionale Array wurde hierbei als Zeiger auf sein erstes Element übergeben und zusätzlich die Angaben zu seinen Dimensionen in der Argumentenliste der Funktion hinzugefügt.
/** Matrix Multiplikation mit ausgelagerter print-Funktion * (m x l)-Matrix = (m x n)-Matrix * (n x l)-Matrix * Spezialfall * (m x m)-Matrix = (m x n)-Matrix * (n x m)-Matrix * C[m][m] = A[m][n] * B[n][m] * hier speziell eine (3 x 5)-Matrix A und eine (5 x 3)-Matrix B **/ #include <iostream> // Ein- und Ausgabebibliothek //Ausgelagerte Funktion, Ausgabe der (m x n)-Matrix im Terminal void print_Matrix(int* M, int dim_1, int dim_2){ // Anfang des Anweisungsblockes for(int i=0; i < dim_1; ++i){ // Anfang Schleife 1 (Zeilen der Matrix) printf("| "); for(int j=0; j < dim_2; ++j){ // Anfang Schleife 2 (Spalten der Matrix) printf("%3i ", M[i*dim_2 +j]); // Ausgabe des Matrixwertes M_{ij} } // Ende der 2.Schleife printf("| \n"); } // Ende der 1.Schleife } // Ende der Funktion int main(){ // Hauptfunktion const int m = 3; // Dimension der Zeilen der Matrix A const int n = 5; // Dimension der Spalten der Matrix A int A[m][n] = { { 1, 2, 3, 4, 5}, {21,22,23,24,25}, {51,52,53,54,55} }; // Definition eines (3x5)-Integer-Arrays, (3x5)-Matrix int B[n][m] = { { 1, 2, 3}, { 4, 5, 6}, { 7, 8, 9}, {10,11,12}, {13,14,15} }; // Definition eines (5x3)-Integer-Arrays, (5x3)-Matrix int C[m][m]; // Deklaration eines (3x3)-Integer-Arrays, (3x3)-Matrix // Matrix Multiplikation C = A * B for(int i=0; i < m; ++i){ // Anfang Schleife 1 (Zeilen der Matrix C) for(int j=0; j < m; ++j){ // Anfang Schleife 2 (Spalten der Matrix C) C[i][j] = 0; // Anfangs-Initialisierung von C_{ij} for(int k=0; k < n; ++k){ // Anfang Schleife 3 (Summationsschleife) C[i][j] = C[i][j] + A[i][k] * B[k][j]; // Matrix Multiplikation } // Ende der 3.Schleife } // Ende der 2.Schleife } // Ende der 1.Schleife printf("\nMatrix A: \n"); print_Matrix(&A[0][0], m, n); // Aufruf der Funktion, Matrix A, (m x n)-Matrix printf("\nMatrix B: \n"); print_Matrix(&B[0][0], n, m); // Aufruf der Funktion, Matrix B, (n x m)-Matrix printf("\nDie Matrix Multiplikation ergibt C = A * B : \n"); print_Matrix(&C[0][0], m, m); // Aufruf der Funktion, Matrix C, (m x m)-Matrix }
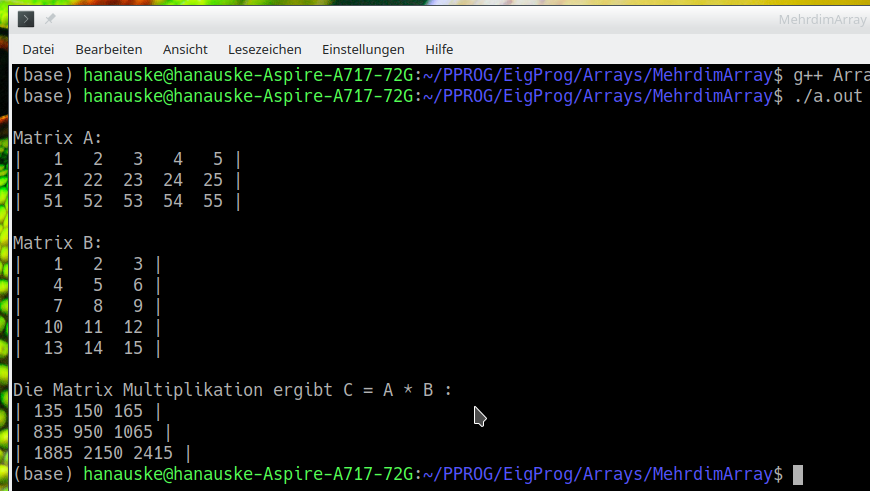
Die Funktion "void print_Matrix(int* M, int dim_1, int dim_2){ ... }" wird dann im Hauptprogramm dreimal aufgerufen, um die Matrizen ${\bf \cal A}$, ${\bf \cal B}$ und ${\bf \cal C}$ darzustellen. Man beachte hierbei, dass beim Aufruf der Funktion im Hauptprogramm (z.B. für die Matrix ${\bf \cal A}$: print_Matrix(&A[0][0], m, n);) die Adresse des ersten Elementes der Matrix übergeben wird (&A[0][0]) - man hätte hier auch '&A[0]' schreiben können, jedoch nicht '&A'. Das folgende Bild veranschaulicht die Terminalausgabe.
Die oben definierte Funktion hat jedoch mehrere Nachteile und wir werden im Folgenden zwei verbesserte Varianten der print_Matrix(..)-Funktion vorstellen, die modernere C++-Konzepte verwenden. Ein wichtiger Anwendungsbereich der Objekt-orientierten Programmierung besteht darin, C++-Klassen und Funktionen zu erstellen, die von anderen Programmierern verwendet werden können. Die Anwendung der geschriebenen Programme sollte dabei möglichst einfach und fehlerfrei sein. Die Anwendung unserer Funktion "void print_Matrix(int* M, int dim_1, int dim_2){ ... }" ist jedoch nicht so einfach und gerade bei der Angabe der Dimensionen des Arrays (int dim_1, int dim_2) kann der Anwender einen Fehler machen, der dann das Programm zum Absturz bringen könnte. Auch ist die print_Matrix Funktion auf ganzzahlige Matrizen beschränkt, was dem Anwender vielleicht nicht klar ist.
In dem folgenden C++ Programm wurde die Methode Call-by-Reference verwendet und die oben genannten Nachteile der print_Matrix Funktion sind behoben. Das Programm wurde von Herrn Johannes Misch erstellt und es verwendet, in einer eleganten Template-Funktion, zwei ineinander geschachtelte bereichsbasierte for-Schleifen. Beim Aufrufen der Funktion aus dem Hauptprogramm 'print_Matrix( A );' muss der Anwender lediglich das C++-Array der Matrix in die Argumentenliste der Funktion schreiben und abhängig vom Datentyp der Matrixelemente und der Dimension des Arrays verwendet die Template-Funktion den geeigneten Matrixtyp.
/** Matrix Multiplikation mit ausgelagerter print-Funktion * (m x l)-Matrix = (m x n)-Matrix * (n x l)-Matrix * Spezialfall * (m x m)-Matrix = (m x n)-Matrix * (n x m)-Matrix * C[m][m] = A[m][n] * B[n][m] * hier speziell eine (3 x 5)-Matrix A und eine (5 x 3)-Matrix B * Diese Version benutzt eine Template-Funktion und bereichbasierte for-Schleifen zur Terminalausgabe der Matrix * Diese Version des C++ Programm wurde von Johannes Misch erstellt ( misch@itp.uni-frankfurt.de ) **/ #include <iostream> #include <iomanip> // Dies ist ein funktions-template. Eine Blaupause fuer funktionen die der Compiler verwendet um funktionen nach bedarf zu erstellen // Die funktion akzeptiert ein array der form T arr[a][b]; // sie bestimmt sowohl den type 'T', als auch die groesse des arrays automatisch anhand ihres arguments template <typename T, std::size_t a, std::size_t b> void print_Matrix( const T (&M)[a][b] ) { // range-based for loops iterieren ueber alle elemente einer collection, in diesem fall ueber alle alle zeilen der matrix // const heisst dass wir die zeile nicht modifizieren // auto sagt dem compiler, dass er den typ automatisch anhand des initializers bestimmen soll // es ist eine reference, weil wir keine Kopie der zeile haben wollen, sondern nur lesen for ( const auto& row : M ) { std::cout << "| "; for ( const auto value : row ) // diesmal machen wir eine kopie, da dies fuer die meisten fundamentalen typen (wie z.b. int) besser ist { std::cout << std::setw(8); //wir setzen die breite der naechsten ausgabe auch mindestens 8 zeichen. Dadurch wird die matrix "schoen" dargestellt std::cout << value << ' '; } std::cout << "|\n"; } } int main() { constexpr int m = 3; // Dimension der Zeilen der Matrix A constexpr int n = 5; // Dimension der Spalten der Matrix A //constexpr bezeichnet eine compile-time konstante. Built-in arrays muessen eine compile-time konstante groesse haben. // Definition eines (3x5)-Integer-Arrays, (3x5)-Matrix // 'const' heisst das wir dieses array waehrend der restlichen laufzeit nicht mehr aendern werden // man sollte i.A. immer 'const' verwenden wenn man nicht vor hat die variable zu veraendern const int A[m][n] = { { 1, 2, 3, 4, 5 }, { 21, 22, 23, 24, 25 }, { 51, 52, 53, 54, 55 } }; // Definition eines (5x3)-Integer-Arrays, (5x3)-Matrix const int B[n][m] = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 }, { 10, 11, 12 }, { 13, 14, 15 } }; // Definition eines (3x3)-Integer-Arrays, (3x3)-Matrix. Automatische initializierung mit 0 // Dieses array is nicht 'const' da es das ergebnis enthalten wird int C[m][m] = {}; // eine leere initializer-list fuert dazu das alle werte im array mit 0 initialized werden // Matrix Multiplikation C = A * B for ( int i=0; i < m; ++i ) { for ( int j=0; j < m; ++j ) { for ( int k=0; k < n; ++k ) { C[i][j] += A[i][k] * B[k][j]; } } } std::cout << "\nMatrix A: \n"; print_Matrix( A ); // Dies ruft print_Matrix<int,3,5> auf. Der compiler bestimmt diese parameter automatisch anhand des types von 'A' std::cout << "\nMatrix B: \n"; print_Matrix( B ); std::cout << "\nDie Matrix Multiplikation ergibt C = A * B : \n"; print_Matrix( C ); }
In modernen C++-Programme bevorzugt man hingegen oft das sogenannte C++ Container Konzept (siehe C++ Container und die vector Klasse der Standardbibliothek). Vektoren und Matrizen können dabei z.B. mittels der Standard-Container <vector> bzw. <array> dargestellt werden.
In dem folgenden C++ Programm wurden die Integer-Matrizen mittels einer Vektor-Matrix der Standardbibliothek dargestellt (Matrix A z.B. vector<vector<int>> A = {...};). Die Initialisierung der Matrizen A und B erfolgt ebenfalls direkt mit Initialisierungslisten, wobei die Dimensionen der Matrizen bei einem solchen <vector>-Konstrukt nicht fest sind und gegebenenfalls im Laufe des Programmes verändert werden können. Nach der Definition der Matrizen A und B werden deren Dimensionen automatisch bestimmt und müssen nicht 'per Hand' extra definiert werden (z.B. size_t m = A.size(); ). Der hierbei verwendete neue Typ size_t ist ein vorzeichenloser Ganzzahltyp, der für Container-Größen und Indizes in der Standardbibliothek verwendet wird. Seine Größe hängt von der Plattform ab (z. B. 32 oder 64 Bit). Die bei der Matrixmultiplikation verwendete Indexschreibweise bleibt unverändert. Die ausgelagerte Funktion zur Terminalausgabe einer Integer-Matrix nimmt die Referenz 'const vector<vector<int>>& M' der Matrix als Parameter, was typsicher ist und einen direkten Zugriff auf die Matrixelemente erlaubt.
/** Matrix Multiplikation mit ausgelagerter print-Funktion * Verwendung einer int Vektor-Matrix des Containers der Standardbibliothek * (m x l)-Matrix = (m x n)-Matrix * (n x l)-Matrix * hier speziell eine (3 x 5)-Matrix A und eine (5 x 4)-Matrix B **/ #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <iostream> // Ein- und Ausgabebibliothek #include <iomanip> // Fuer setw(..) noetig using namespace std; // Benutze den Namensraum std //Ausgelagerte Funktion, Ausgabe der Integer (m x n)-Matrix im Terminal void print_Matrix(const vector<vector<int>>& M) { // Anfang des Anweisungsblockes for (const auto& zeile : M) { // Bereichsbasierte for-Schleife, Iteration über die Zeilen der Matrix cout << "| "; for (int val : zeile) { // Bereichsbasierte for-Schleife, Iteration über die Spalten der Matrix cout << setw(3) << val << " "; } cout << "|\n"; } } int main(){ // Hauptfunktion // Definition einer int Vektor-Matrix, (3x5)-Matrix A vector<vector<int>> A = { {1, 2, 3, 4, 5}, {21, 22, 23, 24, 25}, {51, 52, 53, 54, 55} }; // Definition einer int Vektor-Matrix, (5x4)-Matrix B vector<vector<int>> B = { {1, 2, 3, 100}, {4, 5, 6, 110}, {7, 8, 9, 120}, {10, 11, 12, 130}, {13, 14, 15, 140} }; size_t m = A.size(); // Dimension der Zeilen der Matrix A size_t n = A[0].size(); // Dimension der Spalten der Matrix A size_t l = B[0].size(); // Dimension der Spalten der Matrix B // Definition einer int Vektor-Matrix, (3x4)-Matrix C mit Nullen vector<vector<int>> C(m, vector<int>(l, 0)); // Matrixmultiplikation C = A * B for (size_t i = 0; i < m; ++i) { for (size_t j = 0; j < l; ++j) { for (size_t k = 0; k < n; ++k) { C[i][j] += A[i][k] * B[k][j]; } } } // Ausgabe der Matrizen cout << "\nMatrix A:\n"; print_Matrix(A); cout << "\nMatrix B:\n"; print_Matrix(B); cout << "\nDie Matrixmultiplikation ergibt C = A * B:\n"; print_Matrix(C); }
Die im oberen Programm verwendete Funktion kann man auch in Form einer Template-Funktion schreiben um auch eine Ausgabe von unterschiedlichen Matrix-Typen (z. B. double statt int) zu unterstützen (siehe hierfür das C++-Programm Array_mehrdim_funktion_stdvector_template.cpp).
Abschließend sollte noch erwähnt werden, dass das obere Programm vom Benutzer auch Fehlerhaft angewendet werden kann und der Code keine Prüfungen für leere Matrizen, unregelmäßige Matrizen oder Kompatibilität der Dimensionen bei der Matrixmultiplikation enthält.