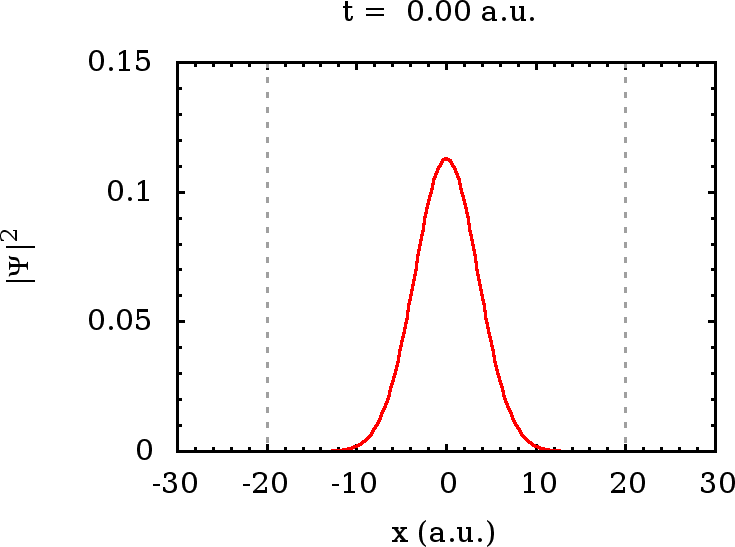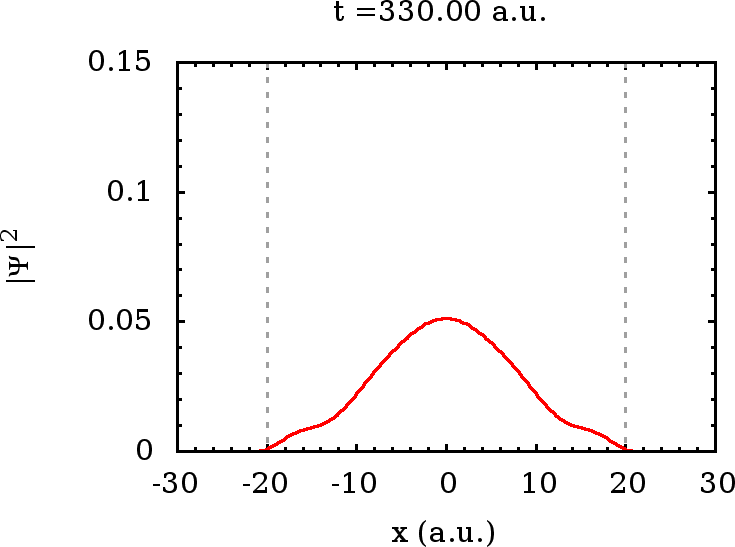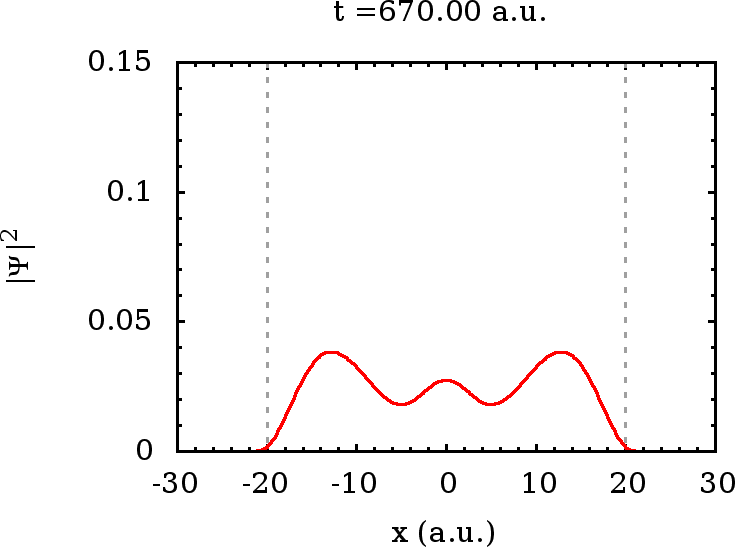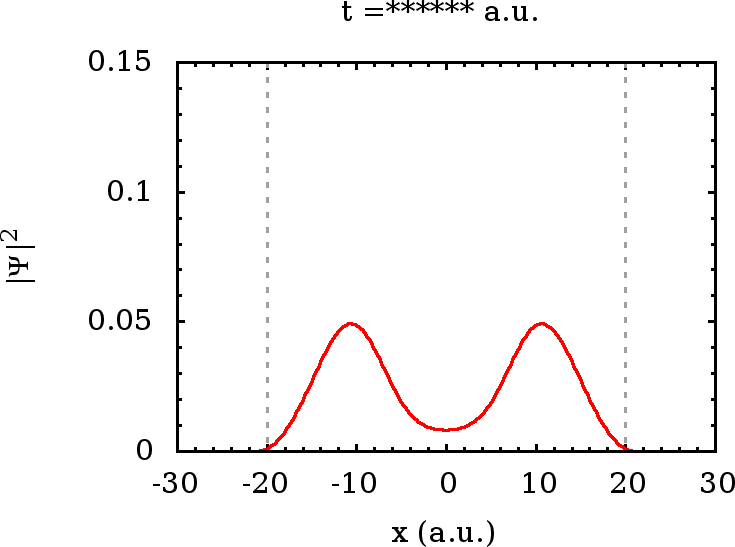
Um eine Vorstellung über die Natur von Wellenpaketen zu erhalten, die
sich aus der Überlagerung gebundener Zustände ergeben, simulieren wir
schließlich noch einen anfang (ebenfalls näherungsweise Gaußförmig
gewähltes) auf das Innere des Topfes konzentriertes Wellenpaket, das
sich ausschließlich aus den gebundenen Zuständen zusammensetzt. Wie
man aus Abb. 4 sieht, gibt es im gegebenen Falle 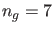 gebundene Zustände mit positiver und
gebundene Zustände mit positiver und 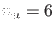 mit negativer
Parität. Das Wellenpaket besitzt also die folgende Gestalt
mit negativer
Parität. Das Wellenpaket besitzt also die folgende Gestalt
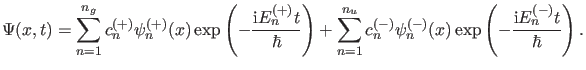 |
(80) |
Die Koeffizienten 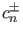 wurden als die entsprechenden
,,verallgemeinerten Fourierkoeffizienten” eines Gaußschen Wellenpakets
wurden als die entsprechenden
,,verallgemeinerten Fourierkoeffizienten” eines Gaußschen Wellenpakets
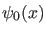 bestimmt:
bestimmt:
![$\displaystyle c_n^{\pm} = \int_{-\infty}^{\infty} \dd x [\psi_n^{\pm}(x)]^* \psi_0(x).$](img254.png) |
(81) |
Freilich ist dann (80) für 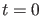 nicht genau das Gaußpaket
nicht genau das Gaußpaket
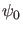 , da zu dessen exakter Entwicklung nach Energieeigenzuständen
auch die ungebundenen Zustände beitragen würden. Wir wollen hier aber
gerade den Fall eines ausschließlich aus gebundenen Zuständen
zusammengesetzten Wellenpaketes studieren. Freilich haben wir das
Wellenpaket (80) wieder auf
, da zu dessen exakter Entwicklung nach Energieeigenzuständen
auch die ungebundenen Zustände beitragen würden. Wir wollen hier aber
gerade den Fall eines ausschließlich aus gebundenen Zuständen
zusammengesetzten Wellenpaketes studieren. Freilich haben wir das
Wellenpaket (80) wieder auf 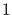 normiert.
normiert.
Wie wir sehen, verhält sich ein solches Wellenpaket wie eine stehende
Welle, die auch im Bereich 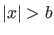 nicht strikt verschwindet, wohin ein
klassisches Teilchen mit einer Energie
nicht strikt verschwindet, wohin ein
klassisches Teilchen mit einer Energie 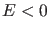 aufgrund des
Energieerhaltungssatzes nicht gelangen könnte. Dies ist wieder der
bereits oben bei der Diskussion der Potentialstufe erwähnte
quantenmechanische Tunneleffekt.
aufgrund des
Energieerhaltungssatzes nicht gelangen könnte. Dies ist wieder der
bereits oben bei der Diskussion der Potentialstufe erwähnte
quantenmechanische Tunneleffekt.
Hendrik van Hees
2019-11-08
![]() gebundene Zustände mit positiver und
gebundene Zustände mit positiver und ![]() mit negativer
Parität. Das Wellenpaket besitzt also die folgende Gestalt
mit negativer
Parität. Das Wellenpaket besitzt also die folgende Gestalt