Wir beginnen mit der Suche nach Energieeigenwerten mit geraden
Energieeigenfunktionen und betrachten zunächst die Möglichkeit, daß
gebundene Zustände auftreten, also Energieeigenwerte 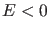 existieren. Setzen wir wieder
existieren. Setzen wir wieder
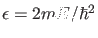 und
und
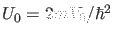 , haben wir
, haben wir
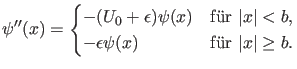 |
(58) |
Es ist weiter von vornherein klar, daß
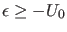 und also
und also
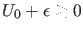 sein muß. Da die Wellenfunktion gerade sein soll
und im Unendlichen nicht exponentiell wachsen darf, ist die Lösung
eindeutig durch
sein muß. Da die Wellenfunktion gerade sein soll
und im Unendlichen nicht exponentiell wachsen darf, ist die Lösung
eindeutig durch
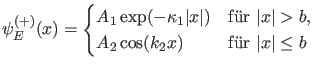 |
(59) |
mit
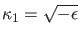 und
und
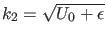 gegeben. Die Wellenfunktion muß bei
gegeben. Die Wellenfunktion muß bei  mitsamt ihrer ersten
Ableitung stetig sein. Das ergibt das homogene lineare Gleichungssystem
mitsamt ihrer ersten
Ableitung stetig sein. Das ergibt das homogene lineare Gleichungssystem
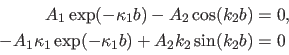 |
(60) |
als Bedingung für die Konstanten 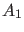 und
und 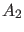 . Damit dieses
Gleichungssystem von der trivialen Lösung
. Damit dieses
Gleichungssystem von der trivialen Lösung 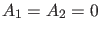 verschiedene
Lösungen haben kann, muß die Determinante der Koeffizientenmatrix
verschwinden, und das führt nach ein paar einfachen Umformungen auf die
Bedingung
verschiedene
Lösungen haben kann, muß die Determinante der Koeffizientenmatrix
verschwinden, und das führt nach ein paar einfachen Umformungen auf die
Bedingung
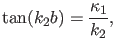 d.h. d.h. 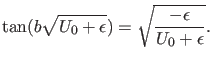 |
(61) |
Die letzte Form der Gleichung zeigt, daß es sich um eine Bedingung an
die Energieeigenwerte
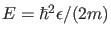 handelt.
handelt.
Diese Gleichung läßt sich nicht geschlossen lösen, aber wir können
sie leicht graphisch analysieren. Dazu führen wir die neue Variable
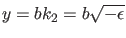 ein. Dann schreibt sich die Gleichung
ein. Dann schreibt sich die Gleichung
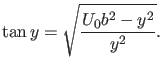 |
(62) |
Offenbar muß also
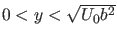 sein, und wir müssen
untersuchen, wo Schnittpunkte zwischen den Graphen der Funktionen auf
der linken und rechten Seite existieren. Deren
sein, und wir müssen
untersuchen, wo Schnittpunkte zwischen den Graphen der Funktionen auf
der linken und rechten Seite existieren. Deren 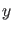 -Werte sind dann
offenbar die gesuchten Lösungen. Betrachten wir dazu den linken Plot in
Abb. 4.
-Werte sind dann
offenbar die gesuchten Lösungen. Betrachten wir dazu den linken Plot in
Abb. 4.
Abbildung:
Zur graphischen Lösung der
Eigenwertbestimmungsgleichungen für gerade (links) und ungerade
Eigenfunktionen rechts, cf. Gln. (61) und
(69).
|
|
Hier haben wir 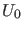 und
und 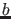 gerade so gewählt, daß
gerade so gewählt, daß
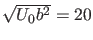 . Wir werden diese Wahl für alle unten gezeigten Simulationen
von Wellenpaketen beibehalten. In schwarz sind die positiven Zweige des
Tangens aufgetragen in rot der Graph der Funktion auf der rechten Seite
von Gl. (62). Da diese Funktion monoton fällt und für
. Wir werden diese Wahl für alle unten gezeigten Simulationen
von Wellenpaketen beibehalten. In schwarz sind die positiven Zweige des
Tangens aufgetragen in rot der Graph der Funktion auf der rechten Seite
von Gl. (62). Da diese Funktion monoton fällt und für
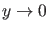 divergiert, gibt es für jeden Wert von
divergiert, gibt es für jeden Wert von
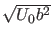 wenigstens einen Schnittpunkt (und also einen Energieeigenwert) mit dem
Zweig des Tangens im Bereich
wenigstens einen Schnittpunkt (und also einen Energieeigenwert) mit dem
Zweig des Tangens im Bereich
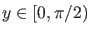 . Weitere Eigenwerte sind
möglich, wenn
. Weitere Eigenwerte sind
möglich, wenn
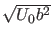 größer ist, und zwar gibt es genau
einen Schnittpunkt mit jedem Zweig des Tangens, der im
Definitionsbereich
größer ist, und zwar gibt es genau
einen Schnittpunkt mit jedem Zweig des Tangens, der im
Definitionsbereich
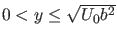 liegt. Wie aus der
allgemeinen Diskussion zu erwarten, sind also die Energieeigenwerte zu
gebundenen Zuständen diskret.
liegt. Wie aus der
allgemeinen Diskussion zu erwarten, sind also die Energieeigenwerte zu
gebundenen Zuständen diskret.
Man überlegt sich leicht, daß die Anzahl der Energieeigenwerte mit
geraden Eigenfunktionen
![$\displaystyle n_+=\left[\frac{\sqrt{U_0 b^2}}{\pi} \right]+1$](img217.png) |
(63) |
ist, wobei ![$ [x]$](img218.png) für die größte natürliche Zahl, die
für die größte natürliche Zahl, die 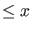 ist,
steht. Dabei fällt die
ist,
steht. Dabei fällt die 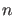 -te Lösung ins Intervall
-te Lösung ins Intervall
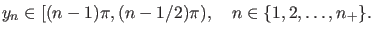 |
(64) |
Damit lassen sich sämtliche Lösungen der Gleichung (61)
numerisch mittels des Bisektionsverfahrens zuverlässig berechnen. Die
dazugehörigen Eigenfunktionen sind dann durch Lösung einer der beiden
Gleichungen von (60) als die Funktion (59) gegeben:
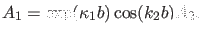 |
(65) |
Da die Determinante für jeden Eigenwert verschwindet, ist dann die
andere Gleichung von (60) automatisch ebenfalls erfüllt. Die
Konstante 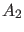 ist schließlich durch die Normierungsbedingung
ist schließlich durch die Normierungsbedingung
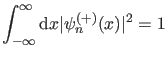 |
(66) |
bestimmt. Das Integral existiert mit Sicherheit, da die Wellenfuntionen
im Unendlichen exponentiell abfallen. Nach Auswertung desselben gelangt
man schließlich auf
![$\displaystyle A_2=\left [ b+\frac{\cos^2(k_2 b)}{\kappa_1} + \frac{\sin(2 k_2 b)}{2 k_2} \right ]^{-1/2}.$](img224.png) |
(67) |
Hendrik van Hees
2019-11-08
![]() existieren. Setzen wir wieder
existieren. Setzen wir wieder
![]() und
und
![]() , haben wir
, haben wir
![]() ein. Dann schreibt sich die Gleichung
ein. Dann schreibt sich die Gleichung
![]() und
und ![]() gerade so gewählt, daß
gerade so gewählt, daß
![]() . Wir werden diese Wahl für alle unten gezeigten Simulationen
von Wellenpaketen beibehalten. In schwarz sind die positiven Zweige des
Tangens aufgetragen in rot der Graph der Funktion auf der rechten Seite
von Gl. (62). Da diese Funktion monoton fällt und für
. Wir werden diese Wahl für alle unten gezeigten Simulationen
von Wellenpaketen beibehalten. In schwarz sind die positiven Zweige des
Tangens aufgetragen in rot der Graph der Funktion auf der rechten Seite
von Gl. (62). Da diese Funktion monoton fällt und für
![]() divergiert, gibt es für jeden Wert von
divergiert, gibt es für jeden Wert von
![]() wenigstens einen Schnittpunkt (und also einen Energieeigenwert) mit dem
Zweig des Tangens im Bereich
wenigstens einen Schnittpunkt (und also einen Energieeigenwert) mit dem
Zweig des Tangens im Bereich
![]() . Weitere Eigenwerte sind
möglich, wenn
. Weitere Eigenwerte sind
möglich, wenn
![]() größer ist, und zwar gibt es genau
einen Schnittpunkt mit jedem Zweig des Tangens, der im
Definitionsbereich
größer ist, und zwar gibt es genau
einen Schnittpunkt mit jedem Zweig des Tangens, der im
Definitionsbereich
![]() liegt. Wie aus der
allgemeinen Diskussion zu erwarten, sind also die Energieeigenwerte zu
gebundenen Zuständen diskret.
liegt. Wie aus der
allgemeinen Diskussion zu erwarten, sind also die Energieeigenwerte zu
gebundenen Zuständen diskret.