Die Bindungszustände mit ungerader Wellenfunktion finden sich in ganz
analoger Weise wie eben für die geraden Wellenfunktionen
besprochen. Es gilt
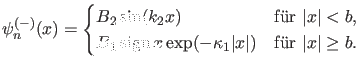 |
(68) |
Die Stetigkeit der Wellenfunktion und ihrer Ableitung bei  führt
wieder auf ein homogenes lineares Gleichungssystem für die
Koeffizienten
führt
wieder auf ein homogenes lineares Gleichungssystem für die
Koeffizienten 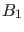 und
und 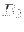 . Damit nichttriviale Lösungen existieren,
müssen wir wieder das Verschwinden der Koeffizientenmatrix
verlangen. Dies führt nach Einführung der obigen Variablen
. Damit nichttriviale Lösungen existieren,
müssen wir wieder das Verschwinden der Koeffizientenmatrix
verlangen. Dies führt nach Einführung der obigen Variablen 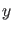 schließlich auf die Bestimmungsgleichung
schließlich auf die Bestimmungsgleichung
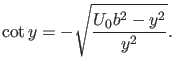 |
(69) |
Analog zur Diskussion für die geraden Wellenfunktionen führt die
Betrachtung des rechten Plots in Abb. 4 auf die Anzahl der
Energieeigenwerte mit ungerader Energieeigenfunktion, nämlich
![$\displaystyle n_u= \begin{cases}0 & \text{falls $\sqrt{U_0 b^2}<\pi/2$},\\ \lef...
...-\frac{1}{2} \right] +1 & \text{falls $\sqrt{U_0 b^2} \geq \pi/2$}. \end{cases}$](img228.png) |
(70) |
Falls
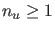 liegen die Lösungen für
liegen die Lösungen für 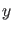 stets in den
Intervallen
stets in den
Intervallen
![$\displaystyle y_n \in \left [ \frac{2n-1}{2} \pi, n \pi \right ]$](img230.png) für für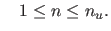 |
(71) |
Auch hier ist wieder das numerische Auffinden aller Lösungen mit Hilfe
der Bisektionsmethode problemlos möglich.
Für den 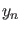 entsprechenden Energieeigenwert ergibt sich dann aus der
Stetigkeits- und Normierungsbedingung für die Koeffizienten
entsprechenden Energieeigenwert ergibt sich dann aus der
Stetigkeits- und Normierungsbedingung für die Koeffizienten
![\begin{displaymath}\begin{split}B_1 &= \exp(\kappa_1 b) \sin(k_2 b) B_2, \\ B_2 ...
...a_1} - \frac{\sin(2 k_2 b)}{2 k_2} \right ]^{-1/2}. \end{split}\end{displaymath}](img233.png) |
(72) |
Hendrik van Hees
2019-11-08
![]() entsprechenden Energieeigenwert ergibt sich dann aus der
Stetigkeits- und Normierungsbedingung für die Koeffizienten
entsprechenden Energieeigenwert ergibt sich dann aus der
Stetigkeits- und Normierungsbedingung für die Koeffizienten