• Einführung in die Programmierung für Studierende der Physik

• von Dr.phil.nat.Dr.rer.pol. Matthias Hanauske

Theorie: Numerische Integration

Wir betrachten in diesem Unterpunkt die Methode der numerischen Integration mittels der "Geschlossenen Newton-Cotes Gleichungen" (closed Newton-Cotes formulars). Die Vorgehensweise der Herleitung dieser Gleichungen erfolgt, indem man die zu integrierende Funktion $f(x)$ in ein Lagrange Polynom vom Grade N ($P_N(x)$) entwickelt (siehe Anwendungsbeispiel: Interpolation und Polynomapproximation) und dann durch analytische Integration zur Approximation gelangt, die für $N=1$ in die Trapez-Regel, für $N=2$ in die Simpson's-Regel und für $N=3$ in die Simpson's-3/8-Regel übergehen.
Wir möchten das folgende bestimmte Integral numerisch approximieren: $$ \begin{equation} \int_a^b f(x) \, dx \approx \sum_{i=0}^N c_i \,f(x_i) \quad, \end{equation} $$ wobei man das Integrationsintervall in $N+1$ äquidistante Punkte unterteilt: $x_0=a$, $x_N=b$ und $x_i=a+i\cdot(b-a)/N=a+i\cdot h$ mit ($i=0,1,2,..,N$). Im Folgenden wollen wir die jeweiligen Gleichungen mittels der Methode der Lagrange Polynome ($P_N(x)$) herleiten. Das N-te Lagrange Polynom $P_N(x)$ einer Funktion ist wie folgt definiert: $$ \begin{equation} P_N(x) = \sum_{k=0}^N f(x_k) \cdot L_{N,k}(x) \quad, \end{equation} $$ mit $$ \begin{equation} L_{N,k}(x) = \prod_{i=0 , \, i \neq k}^N \frac{(x-x_i)}{(x_k-x_i)} \quad. \end{equation} $$ Setzt man das Lagrange Polynom $P_N(x)$ in das bestimmte Integral ein, erhält man: $$ \begin{equation} \int_a^b f(x) \, dx \approx \int_a^b \sum_{k=0}^N f(x_k) \cdot L_{N,k}(x) \, dx = \sum_{k=0}^N f(x_k) \cdot \underbrace{\int_a^b L_{N,k}(x) \, dx}_{c_k} := \sum_{k=0}^N f(x_k) \, c_k \quad . \end{equation} $$

Die Trapez-Regel (N=1)

Die einfachste Approximation erhält man mittels eines linearen Lagrange Polynoms $P_1(x)$. Man benutzt dabei lediglich zwei Punkte, nämlich die Grenzen des Intervalls ($x_0=a$ und $x_1=b=x_0+h$ mit $h=(b-a)$). Mittels $P_1(x)$ berechnen wir das folgende bestimmte Integral $$ \begin{equation} \int_a^b f(x) \, dx \approx {\cal I}_1 := \int_{x_0}^{x_1} \sum_{k=0}^1 f(x_k) \cdot L_{1,k}(x) \, dx = \int_{x_0}^{x_1} \sum_{k=0}^1 f(x_k) \cdot \prod_{i=0 , \, i \neq k}^1 \frac{(x-x_i)}{(x_k-x_i)} \, dx \quad, \end{equation} $$ und durch analytische Integration erhält man die folgende Trapez-Regel: $$ \begin{equation} {\cal I}_1 = \frac{(x_1 - x_0)}{2} \cdot \left( f(x_0) + f(x_1) \right) = \frac{h}{2} \cdot \left( f(x_0) + f(x_1) \right) \quad. \end{equation} $$

Die Simpson's-Regel (N=2)

Die Simpson's Approximation erhält man mittels eines quadratischen Lagrange Polynoms $P_2(x)$. Man benutzt dabei drei Punkte, nämlich die Grenzen des Intervalls ($x_0=a$ und $x_2=b =a + 2h$) und einen Wert in der Mitte des Intervalls ($x_1=a + h$) mit $h=(b-a)/2$. Wieder erhält man durch analytische Integration die folgende Simpson's-Regel: $$ \begin{equation} {\cal I}_2 = \frac{h}{3} \cdot \left( f(x_0) + 4 f(x_1) + f(x_2) \right) \end{equation} $$

Die Simpson's-3/8-Regel (N=3)

Die Simpson's-3/8 Approximation erhält man mittels des Lagrange Polynoms $P_3(x)$. Man benutzt dabei vier Punkte, nämlich die Grenzen des Intervalls ($x_0=a$ und $x_3=b =a + 3h$) und zwei zusätzliche Werte ($x_1=a + h$ und $x_2=a + 2h$) mit $h=(b-a)/3$. Man erhält: $$ \begin{equation} {\cal I}_3 = \frac{3 \, h}{8} \cdot \left( f(x_0) + 3 f(x_1) + 3 f(x_2) + f(x_3) \right) \end{equation} $$

Die N=4 Regel

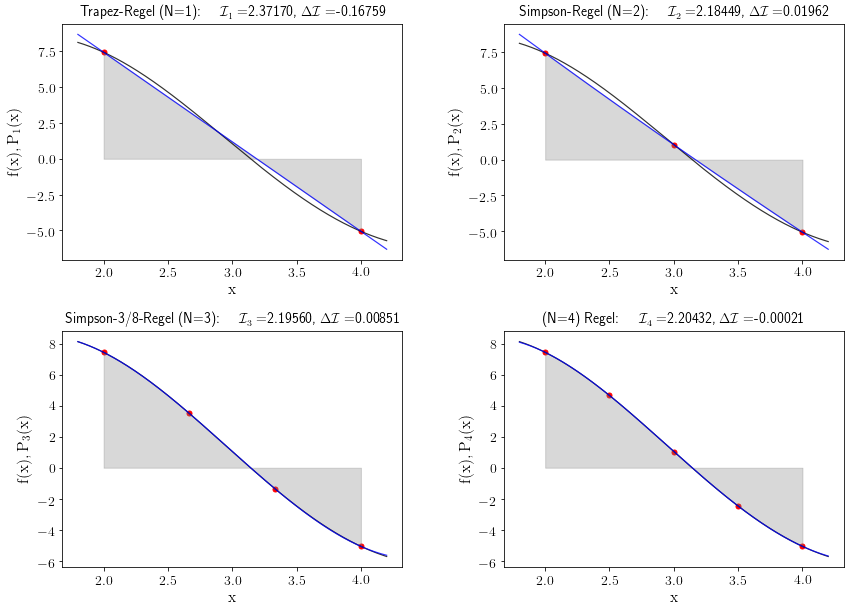
Die $N=4$ Approximation erhält man mittels des Lagrange Polynoms $P_4(x)$. Man benutzt dabei fünf Punkte, nämlich die Grenzen des Intervalls ($x_0=a$ und $x_4=b =a + 4h$) und drei zusätzliche Werte ($x_1=a + h$, $x_2=a + 2h$ und $x_3=a + 3h$) mit $h=(b-a)/4$. Man erhält: $$ \begin{equation} {\cal I}_4 = \frac{2 \, h}{45} \cdot \left( 7 f(x_0) + 32 f(x_1) + 12 f(x_2) + 32 f(x_3) + 7 f(x_4) \right) \end{equation} $$ Wir betrachten nun z.B. die Funktion $f(x)=10 \cdot {\rm sin}(x) \cdot e^{-\frac{x}{10}}$ und approximieren den Wert für das bestimmte Integral $\int_2^4 f(x) \, dx$. Die nebenstehende Abbildung veranschaulicht für dieses Beispiel die unterschiedlichen Integrationsregeln grafisch (näheres siehe Jupyter Notebook NumericalIntegration.ipynb).

Stückweise numerische Integration

Möchte man die Funktion jedoch über ein großes Intervall integrieren, so liefern auch die höheren N-Regeln keine genaue Approximation. Man sollte dann eine iterative, stückweise numerische Integration verwenden, wobei man innerhalb der einzelnen Teilstücke eine der oberen Integrationsregeln verwendet. Wir unterteilen dazu das Integrations-Intervall $[a,b]$ in $n/N$-Teilstücke, wobei $N$ die Ordnung der Integrationsregel und $n$ das kleinste gemeinsame Vielfache von $N$ ist. $$ \begin{eqnarray} \int_a^b f(x) \, dx &=& \sum_{j=1}^{n/N} \int_{x_{N \cdot j-N}}^{x_{N \cdot j}} f(x) \, dx \\ &=& \int_{a=x_0}^{x_N} f(x) \, dx + \int_{x_N}^{x_{N \cdot 2}} f(x) \, dx \, + ... \, + \int_{x_{N \cdot (n/N-1)-N}}^{x_{N \cdot (n/N-1)}} f(x) \, dx + \int_{x_{N \cdot (n/N)-N}}^{x_{N \cdot (n/N)}} f(x) \, dx \,\, =\\ &=& \underbrace{\int_{a=x_0}^{x_N} f(x) \, dx}_{\hbox{Teilintervall 1}} + \underbrace{\int_{x_N}^{x_{N \cdot 2}} f(x) \, dx}_{\hbox{Teilintervall 2}} \, + ... \, + \underbrace{\int_{x_{n-2 \cdot N}}^{x_{n - N}} f(x) \, dx}_{\hbox{Teilintervall } n/N-1} + \underbrace{\int_{x_{n - N}}^{x_{n}} f(x) \, dx}_{\hbox{Teilintervall } n/N} \end{eqnarray} $$ Benutzt man in den Teilintervallen eine der oberen Integrationsregeln, so geht man zu einer stückweisen numerischen Integration über.

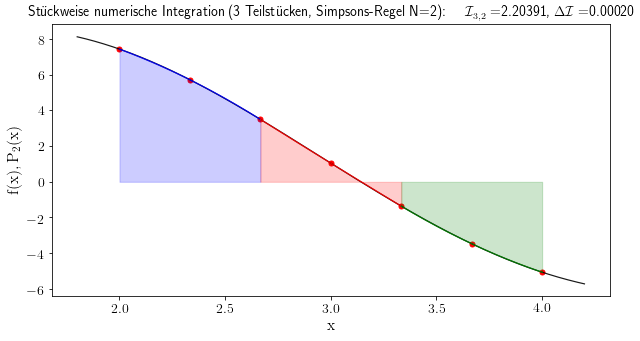
Unterteilen wir z.B. das Integrations-Intervall in drei Teilstücke und benutzen die Simpson's-Regel ($N=2$, $n=6$ $\rightarrow$ $n/N=3$ Teilstücke), so erhalten wir z.B. die folgenden Integrationsterme: $$ \begin{eqnarray} \int_a^b f(x) \, dx &=& \underbrace{\int_{a=x_0}^{x_2} f(x) \, dx}_{\hbox{Teilintervall 1}} + \underbrace{\int_{x_2}^{x_{4}} f(x) \, dx}_{\hbox{Teilintervall 2}} \, + \underbrace{\int_{x_{4}}^{x_{6}} f(x) \, dx}_{\hbox{Teilintervall 3}} \,\, =\\ &=& \int_{a=x_0}^{x_2} \sum_{k=0}^2 f(x_k) \cdot L_{2,k}(x) \, dx + \int_{x_2}^{x_{4}} \sum_{k=2}^4 f(x_k) \cdot L_{2,k}(x) \, dx \, + \int_{x_{4}}^{x_{6}} \sum_{k=4}^6 f(x_k) \cdot L_{2,k}(x) \, dx \,\, =\\ &=& \underbrace{\frac{h}{3} \cdot \left( f(x_0) + 4 f(x_1) + f(x_2) \right)}_{\hbox{Teilintervall 1}} + \underbrace{\frac{h}{3} \cdot \left( f(x_2) + 4 f(x_3) + f(x_4) \right)}_{\hbox{Teilintervall 2}} \, + \underbrace{\frac{h}{3} \cdot \left( f(x_4) + 4 f(x_5) + f(x_6) \right)}_{\hbox{Teilintervall 3}} \,\, =\\ &=& \frac{h}{3} \cdot \left( f(x_0) + 4 f(x_1) + 2 f(x_2) + 4 f(x_3) + 2 f(x_4) + 4 f(x_5) + f(x_6) \right)\quad. \end{eqnarray} $$

Wir betrachten wieder die Funktion $f(x)=10 \cdot {\rm sin}(x) \cdot e^{-\frac{x}{10}}$ und approximieren den Wert für das bestimmte Integral $\int_2^4 f(x) \, dx$. Wir unterteilen das Integrations-Intervall in drei Teilstücke und benutzen die Simpson's-Regel ($N=2$, $n=6$ $\rightarrow$ $n/N=3$ Teilstücke). Die nebenstehende Abbildung veranschaulicht diese stückweise numerische Integration.
Die gesamte Herleitung der Integrationsregeln ist in dem Jupyter Notebook 'NumericalIntegration.ipynb' einsehbar ( View Notebook, Download Notebook).