Numerische Differentiation
In diesem Unterpunkt werden wir die im Jupyter Notebook Das Computeralgebrasystem: Python Jupyter + SymPy ('Jupyter_sympy.ipynb' , View Notebook, Download Notebook) hergeleiteten Differentiationsregeln der numerischen Mathematik in einem C++ Programm anwenden. Im Speziellen werden wir die numerische Ableitung der Funktion $f(x)= 10 \, e^{-x/10} \cdot \hbox{sin}(x)$ mittels der unterschiedlichen Differentiationsformel in einem C++ Programm bestimmen und die Ergebnisse mit der wirklichen, analytisch bestimmbaren Ableitung $f^\prime(x)$ vergleichen.
Die mathematische Definition der Ableitung einer Funktion $f(x)$ an der Stelle $x_0$, der sogenannte Differentialquotient, benutzt die folgende Grenzwert-Formulierung ($h \to 0$):
\[
\begin{equation}
f^\prime(x_0) = \lim \limits_{h \to 0} \frac{f(x_0+h) - f(x_0)}{h} \quad.
\end{equation}
\]
In der numerischen Mathematik hingegen werden mehrere Differentiationsregeln formuliert, die diesen wirklichen Wert der Ableitung approximieren. Die analytische Herleitung dieser Regeln benutzt die Methode der Lagrange Polynome (siehe Anwendungsbeispiel: Interpolation und Polynomapproximation).
Die Differentiationsregeln der numerischen Mathematik
Die im vorigen Unterpunkt hergeleiteten Differentiationsregeln der numerischen Mathematik (siehe Das Computeralgebrasystem: Python Jupyter + SymPy) sind in der folgenden Box nochmals zusammenfassend dargestellt:
\[
\begin{eqnarray}
\hbox{Zweipunkteformel (n=1):}\,\, & \,\,
f^\prime(x_0) \approx \frac{1}{h} \left[ f(x_0 + h) - f(x_0) \right] & \, , \, \hbox{Stützstellen: }\, (x_0, x_0 + h) \\
\hbox{Dreipunkte-Endpunkt-Formel (n=2):}\,\, & \,\,
f^\prime(x_0) \approx \frac{1}{2h} \left[ - 3\,f(x_0) + 4 \, f(x_0 + h) - f(x_0 + 2 \, h) \right] & \, , \, \hbox{Stützstellen: }\, (x_0, x_0 + h, x_0 + 2h) \\
\hbox{Dreipunkte-Mittelpunkt-Formel (n=2):}\,\, & \,\,
f^\prime(x_0) \approx \frac{1}{2h} \left[ f(x_0 + h) - f(x_0 - h) \right] & \, , \, \hbox{Stützstellen: }\, (x_0 - h, x_0, x_0 + h) \\
\hbox{Fünfpunkte-Mittelpunkt-Formel (n=4):}\,\, & \,\,
f^\prime(x_0) \approx \frac{1}{12 \, h} \left[ f(x_0 - 2 \, h) - 8 \, f(x_0 - h) + 8 \, f(x_0 + h) - f(x_0 + 2 \, h) \right] & \, , \, \hbox{Stützstellen: }\, (x_0 - 2h, x_0 - h, x_0, x_0 + h, x_0 + 2h)
\end{eqnarray}
\]
In dem folgenden C++ Programm wird die Ableitung der Funktion $f(x)= 10 \, e^{-x/10} \cdot \hbox{sin}(x)$ an der Stelle $x_0 = 3$ numerisch approximativ berechnet.
Numerical_Differentiation_1.cpp
/* Berechnung der Ableitung f'(x) einer Funktion f(x) * mittels unterschiedlich genauer Approximationen * (Zweipunkteformel, Dreipunkte-Endpunkt-Formel, Dreipunkte-Mittelpunkt-Formel und Fünfpunkte-Mittelpunkt-Formel) */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double x){ // Deklaration und Definition der Funktion f(x) double wert; wert=10*sin(x)*exp(-x/10); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) double f_strich(double x){ // Deklaration und Definition der Ableitung f'(x) der Funktion f(x) double wert; // (f'(x) wird nur zum Vergleich mit den Ergebnissen benoetigt) wert=10*cos(x)*exp(-x/10) - sin(x)*exp(-x/10); // Eigentliche Definition der Ableitung return wert; // Rueckgabewert der Funktion f'(x) } // Ende der Funktion f'(x) int main(){ // Hauptfunktion double x = 3; // Aktueller x-Wert an dem die Ableitung berechnet wird double h=0.01; // Aequidistanter Abstand zwischen den x-Werten die zur numerischen Differentation benutzt werden double f1_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Zweipunkteformel) double f3a_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Dreipunkte-Endpunkt-Formel) double f3b_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Dreipunkte-Mittelpunkt-Formel) double f5_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Fünfpunkte-Mittelpunkt-Formel) f1_strich_p = (f(x+h) - f(x))/h; // Zweipunkteformel f3a_strich_p = (-3*f(x) + 4*f(x+h) - f(x+2*h))/(2*h); // Dreipunkte-Endpunkt-Formel f3b_strich_p = (f(x+h) - f(x-h))/(2*h); // Dreipunkte-Mittelpunkt-Formel f5_strich_p = (f(x-2*h) - 8*f(x-h) + 8*f(x+h) - f(x+2*h))/(12*h); // Fünfpunkte-Mittelpunkt-Formel printf("h-Wert: h = %14.10f \n", h); printf("Wirklicher Wert: f'(x=%5.3f) = %14.10f \n", x, f_strich(x)); // Ausgabe der berechneten Werte printf("Zweipunkteformel: f'(x=%5.3f) = %14.10f , absoluter Fehler: %14.10f \n", x, f1_strich_p, f_strich(x) - f1_strich_p); // Ausgabe der berechneten Werte printf("Dreipunkte-Endpunkt-Formel: f'(x=%5.3f) = %14.10f , absoluter Fehler: %14.10f \n", x, f3a_strich_p, f_strich(x) - f3a_strich_p); // Ausgabe der berechneten Werte printf("Dreipunkte-Mittelpunkt-Formel: f'(x=%5.3f) = %14.10f , absoluter Fehler: %14.10f \n", x, f3b_strich_p, f_strich(x) - f3b_strich_p); // Ausgabe der berechneten Werte printf("Fuenfpunkte-Mittelpunkt-Formel: f'(x=%5.3f) = %14.10f , absoluter Fehler: %14.10f \n", x, f5_strich_p, f_strich(x) - f5_strich_p); // Ausgabe der berechneten Werte } // Ende der Hauptfunktion
Es wird hierbei ein fester Wert von $h=0.01$ angenommen und der Wert der Ableitung $f^\prime(x_0)$ mittels der Zweipunkteformel, Dreipunkte-Endpunkt-Formel, Dreipunkte-Mittelpunkt-Formel und Fünfpunkte-Mittelpunkt-Formel approximiert. Die numerischen Ergebnisse werden dann mit dem analytischen Wert der Ableitung verglichen. Die nebenstehende Abbildung zeigt die Terminalausgabe des Programms.
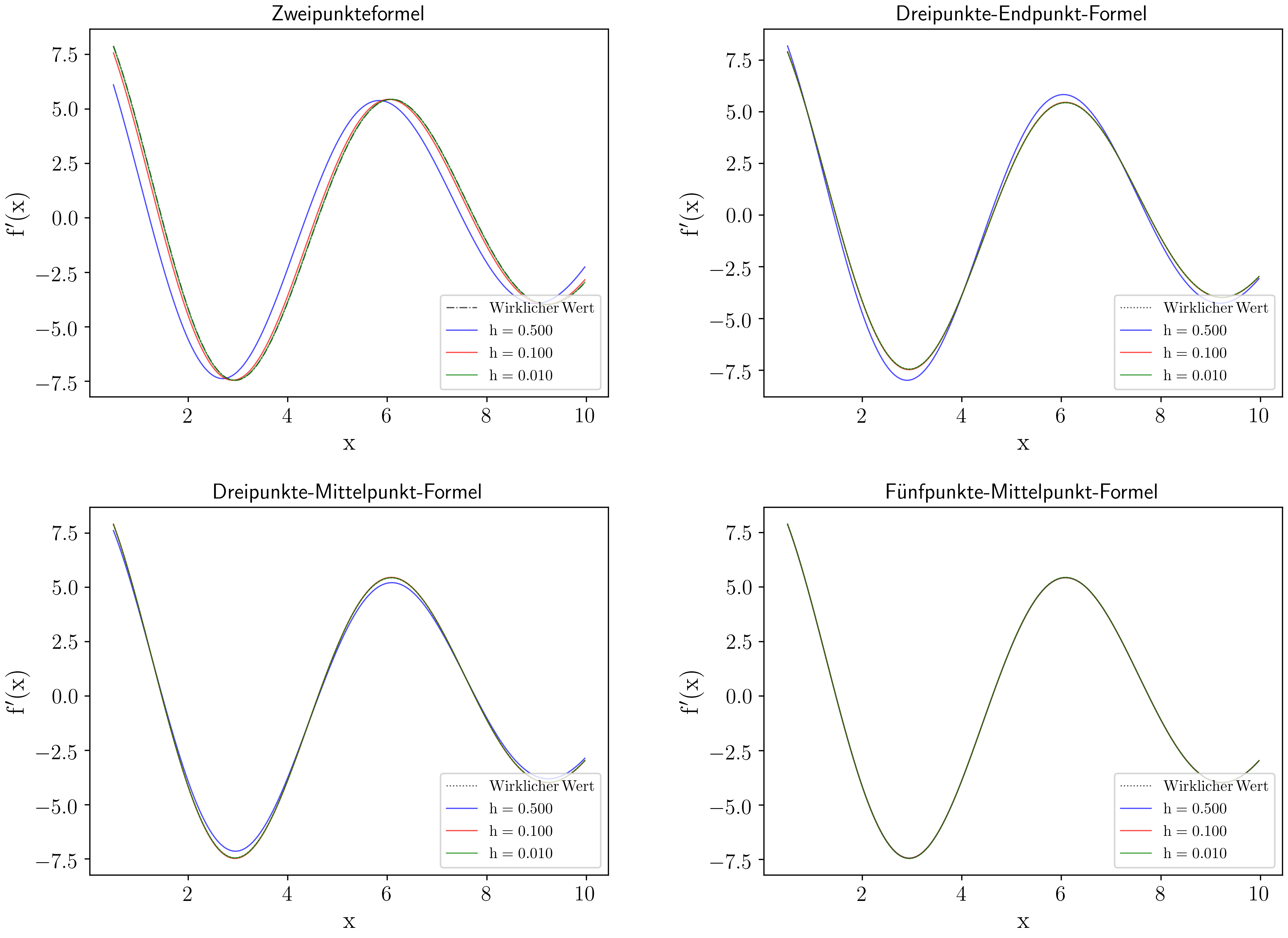
Nun wollen wir uns die Ableitung der Funktion in einem Teilintervall $[a,b]$ ausgeben lassen und die numerischen Lösungen des C++ Programms für unterschiedliche Werte von $h$ mittels eines Python Skriptes visualisieren. Das folgende C++ Programm berechnet $300$ Werte von $f^\prime(x)$ im Teilintervall $[0.5, 10]$ und benutzt dabei drei unterschiedliche $h$-Werte ($h=0.5, 0.1, 0.01$).
Numerical_Differentiation_2.cpp
/* Berechnung der Ableitung f'(x) einer Funktion f(x) * mittels unterschiedlich genauer Approximationen * (Zweipunkteformel, Dreipunkte-Endpunkt-Formel, Dreipunkte-Mittelpunkt-Formel und Fünfpunkte-Mittelpunkt-Formel) * Ausgabe fuer unterschiedliche x-Werte in [a,b] und 3 unterschiedliche h-Werte * Ausgabe zum Plotten mittels Python: "./a.out > Numerical_Differentiation_2.dat */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double x){ // Deklaration und Definition der Funktion f(x) double wert; wert = 10*sin(x)*exp(-x/10); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) double f_strich(double x){ // Deklaration und Definition der Ableitung f'(x) der Funktion f(x) double wert; // (f'(x) wird nur zum Vergleich mit den Ergebnissen benoetigt) wert = 10*cos(x)*exp(-x/10) - sin(x)*exp(-x/10); // Eigentliche Definition der Ableitung return wert; // Rueckgabewert der Funktion f'(x) } // Ende der Funktion f'(x) int main(){ // Hauptfunktion double a = 0.5; // Untergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll double b = 10; // Obergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll int N_xp = 300; // Anzahl der Punkte in die das x-Intervall aufgeteilt wird double dx = (b - a)/N_xp; // Abstand dx zwischen den aequidistanten Punkten des x-Intervalls double x = a - dx; // Aktueller x-Wert double h_list[3]={0.5, 0.1, 0.01}; // Aequidistanter Abstand zwischen den x-Werten die zur numerischen Differentation benutzt werden double h; // Aktueller h-Wert double f1_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Zweipunkteformel) double f3a_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Dreipunkte-Endpunkt-Formel) double f3b_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (3Dreipunkte-Mittelpunkt-Formel) double f5_strich_p; // Deklaration der f'(x)-Ausgabe-Punkte (Fünfpunkte-Mittelpunkt-Formel) printf("# Benutzte h-Werte der Simulation: \n"); // Beschreibung der ausgegebenen Groessen for(int k = 0; k < 3; ++k){ // For-Schleife der Ausgabe der Stuetzstellen x-Werte printf("%10.5f",h_list[k]); // Ausgabe der unterschiedlichen h-Werte } // Ende for-Schleife der Ausgabe printf("\n"); printf("# 0: Index i \n# 1: x-Wert \n# 2: Wirklicher Wert von f'(x) \n"); // Beschreibung der ausgegebenen Groessen printf("# h = %8.7f : \n", h_list[0]); // 0-ter h-Wert printf("# 3: Zweipunkteformel f'(x) \n# 4: Dreipunkte-Endpunkt-Formel \n"); // Beschreibung der ausgegebenen Groessen printf("# 5: Dreipunkte-Mittelpunkt-Formel \n# 6: Fünfpunkte-Mittelpunkt-Formel \n"); // Beschreibung der ausgegebenen Groessen printf("# h = %8.7f : \n", h_list[1]); // 1-ter h-Wert printf("# 7: Zweipunkteformel f'(x) \n# 8: Dreipunkte-Endpunkt-Formel \n"); // Beschreibung der ausgegebenen Groessen printf("# 9: Dreipunkte-Mittelpunkt-Formel \n# 10: Fünfpunkte-Mittelpunkt-Formel \n"); // Beschreibung der ausgegebenen Groessen printf("# h = %8.7f : \n", h_list[2]); // 2-ter h-Wert printf("# 11: Zweipunkteformel f'(x) \n# 12: Dreipunkte-Endpunkt-Formel \n"); // Beschreibung der ausgegebenen Groessen printf("# 13: Dreipunkte-Mittelpunkt-Formel \n# 14: Fünfpunkte-Mittelpunkt-Formel \n"); // Beschreibung der ausgegebenen Groessen for(int i =0; i < N_xp; ++i){ // for-Schleife die ueber die einzelnen Punkte des x-Intervalls geht x=x+dx; // Aktueller x-Wert printf("%3d %14.10f %14.10f",i, x, f_strich(x)); // Ausgaben for(int k = 0; k < 3; ++k){ // For-Schleife die ueber die unterschiedlichen h-Werte h = h_list[k]; // Uebergabe des aktuellen h-Wertes f1_strich_p = (f(x+h) - f(x))/h; // Zweipunkteformel f3a_strich_p = (-3*f(x) + 4*f(x+h) - f(x+2*h))/(2*h); // Dreipunkte-Endpunkt-Formel f3b_strich_p = (f(x+h) - f(x-h))/(2*h); // Dreipunkte-Mittelpunkt-Formel f5_strich_p = (f(x-2*h) - 8*f(x-h) + 8*f(x+h) - f(x+2*h))/(12*h); // Fünfpunkte-Mittelpunkt-Formel printf(" %14.10f %14.10f %14.10f %14.10f", f1_strich_p, f3a_strich_p, f3b_strich_p, f5_strich_p); // Ausgaben der berechneten Groessen } // Ende For-Schleife ueber die unterschiedlichen h-Werte printf("\n"); // Zeilenumbruch } // Ende for-Schleife ueber die einzelnen Punkte des x-Intervalls } // Ende der Hauptfunktion
Das Programm gibt die folgende Tabelle im Terminal aus:
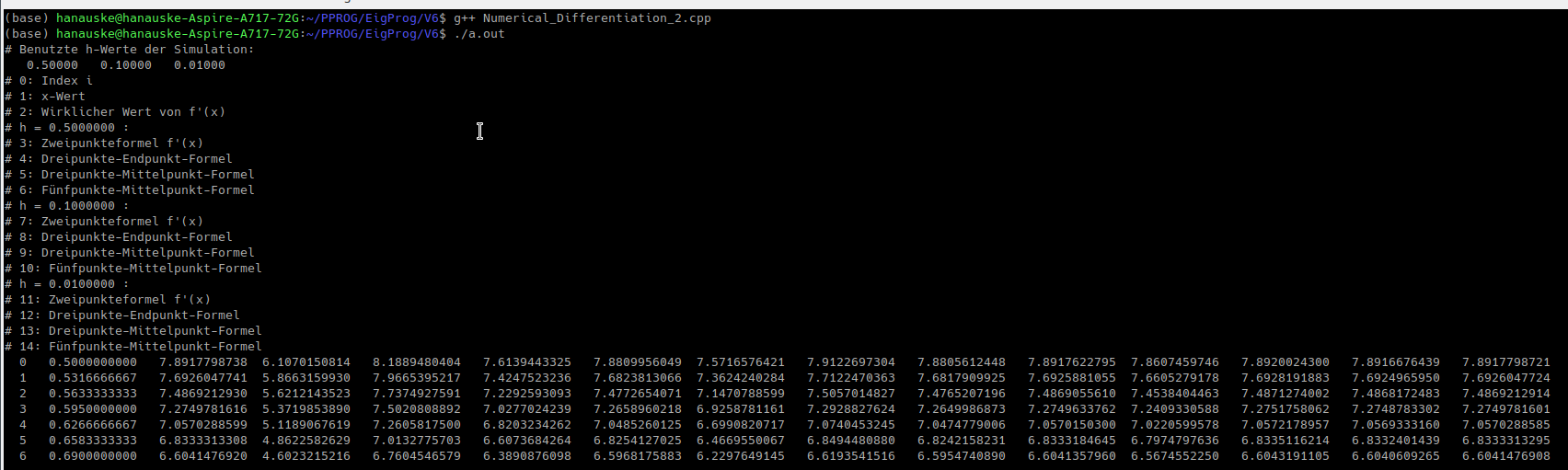
Wir leiten die berechneten Daten wieder in eine Datei "Numerical_Differentiation_2.dat" um und führen das folgende Python Skript aus:
PythonPlot_Numerical_Differentiation_2.py
# Python Programm zum Plotten der berechneten Daten von Numerical_Differentiation_2.cpp import matplotlib # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) import matplotlib.gridspec as gridspec # Mehrere Bilder in einem Plot anordnen # Bildabmessungen usw. params = { 'figure.figsize' : [14,10], 'text.usetex' : True, 'axes.titlesize' : 14, 'axes.labelsize' : 16, 'xtick.labelsize' : 14 , 'ytick.labelsize' : 14 } matplotlib.rcParams.update(params) h_list = np.genfromtxt("./Numerical_Differentiation_2.dat", max_rows=1) # Einlesen der benutzten x-Werte der Stuetzstellen data = np.genfromtxt("./Numerical_Differentiation_2.dat", skip_header=20) # Einlesen der berechneten Daten von Numerical_Differentiation_2.cpp fig = plt.figure() # Hauptbild gs = gridspec.GridSpec(2, 2, width_ratios=[1,1], wspace=0.3, hspace=0.3) # Anordnung der vier Unterbilder ax1 = plt.subplot(gs[0]) ax2 = plt.subplot(gs[1]) ax3 = plt.subplot(gs[2]) ax4 = plt.subplot(gs[3]) ax1.set_title(r'Zweipunkteformel') # Titel der Abbildung in ax1 ax1.set_xlabel(r"$\rm x$") ax1.set_ylabel(r"$\rm f'(x)$") ax2.set_title(r'Dreipunkte-Endpunkt-Formel') # Titel der Abbildung in ax2 ax2.set_xlabel(r"$\rm x$") ax2.set_ylabel(r"$\rm f'(x)$") ax3.set_title(r'Dreipunkte-Mittelpunkt-Formel') # Titel der Abbildung in ax3 ax3.set_xlabel(r"$\rm x$") ax3.set_ylabel(r"$\rm f'(x)$") ax4.set_title(r'Fünfpunkte-Mittelpunkt-Formel') # Titel der Abbildung in ax4 ax4.set_xlabel(r"$\rm x$") ax4.set_ylabel(r"$\rm f'(x)$") l_width=0.8 # Festlegung der Plot-Liniendicke alp=0.7 # Festlegung der Transparenz der Kurven label_0=r'$\rm h='+'{0:.3f}'.format(h_list[0])+'$' # Plot-Labels fuer die unterschiedlichen h-Werte label_1=r'$\rm h='+'{0:.3f}'.format(h_list[1])+'$' label_2=r'$\rm h='+'{0:.3f}'.format(h_list[2])+'$' ax1.plot(data[:,1],data[:,2], color="black", linewidth=l_width, linestyle='-.', alpha=alp, label=r'$\rm Wirklicher \, Wert$') # Plotten auf ax1 ax1.plot(data[:,1],data[:,3], color="blue", linewidth=l_width, linestyle='-', alpha=alp, label=label_0) ax1.plot(data[:,1],data[:,7], color="red", linewidth=l_width, linestyle='-', alpha=alp, label=label_1) ax1.plot(data[:,1],data[:,11], color="green", linewidth=l_width, linestyle='-', alpha=alp, label=label_2) ax2.plot(data[:,1],data[:,2], color="black", linewidth=l_width, linestyle=':', alpha=alp, label=r'$\rm Wirklicher \, Wert$') # Plotten auf ax2 ax2.plot(data[:,1],data[:,4], color="blue", linewidth=l_width, linestyle='-', alpha=alp, label=label_0) ax2.plot(data[:,1],data[:,8], color="red", linewidth=l_width, linestyle='-', alpha=alp, label=label_1) ax2.plot(data[:,1],data[:,12], color="green", linewidth=l_width, linestyle='-', alpha=alp, label=label_2) ax3.plot(data[:,1],data[:,2], color="black", linewidth=l_width, linestyle=':', alpha=alp, label=r'$\rm Wirklicher \, Wert$') # Plotten auf ax3 ax3.plot(data[:,1],data[:,5], color="blue", linewidth=l_width, linestyle='-', alpha=alp, label=label_0) ax3.plot(data[:,1],data[:,8], color="red", linewidth=l_width, linestyle='-', alpha=alp, label=label_1) ax3.plot(data[:,1],data[:,12], color="green", linewidth=l_width, linestyle='-', alpha=alp, label=label_2) ax4.plot(data[:,1],data[:,2], color="black", linewidth=l_width, linestyle=':', alpha=alp, label=r'$\rm Wirklicher \, Wert$') # Plotten auf ax4 ax4.plot(data[:,1],data[:,6], color="blue", linewidth=l_width, linestyle='-', alpha=alp, label=label_0) ax4.plot(data[:,1],data[:,9], color="red", linewidth=l_width, linestyle='-', alpha=alp, label=label_1) ax4.plot(data[:,1],data[:,13], color="green", linewidth=l_width, linestyle='-', alpha=alp, label=label_2) ax1.legend(frameon=True, loc="lower right",fontsize=10) # Anordnung der Legende auf ax1 ax2.legend(frameon=True, loc="lower right",fontsize=10) # Anordnung der Legende auf ax2 ax3.legend(frameon=True, loc="lower right",fontsize=10) # Anordnung der Legende auf ax3 ax4.legend(frameon=True, loc="lower right",fontsize=10) # Anordnung der Legende auf ax4 plt.savefig("Numerical_Differentiation_2.png", dpi=400, bbox_inches="tight", pad_inches=0.05, format="png") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Das Python Skript produziert das folgende Bild:
