Time-Dependent Kohn-Sham Equations
The essence of DFT is the determination of the exact one-particle
density 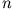 from which any many-particle observable can be
derived. Let us assume we know this density and can calculate it
from a set of
from which any many-particle observable can be
derived. Let us assume we know this density and can calculate it
from a set of 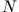 ficticious orbitals
ficticious orbitals
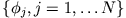
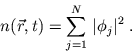 |
(8) |
The ansatz (8) suggests that the orbitals fulfil a
single-particle Schrödinger equation of the form
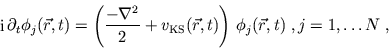 |
(9) |
where the existence of the single-particle potential
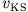 is assumed. (This is discussed in the literature
under the topic v-representability
[9].) If this potential
exists, the Runge-Gross theorem guarantees its uniqueness, i.e.,
there is up to an additive merely time-dependent function exactly
one single-particle potential, which together with the
time-dependent Kohn-Sham (KS)
equations (9) reproduces the
exact one-particle density
is assumed. (This is discussed in the literature
under the topic v-representability
[9].) If this potential
exists, the Runge-Gross theorem guarantees its uniqueness, i.e.,
there is up to an additive merely time-dependent function exactly
one single-particle potential, which together with the
time-dependent Kohn-Sham (KS)
equations (9) reproduces the
exact one-particle density  . Essentially, the KS
equations represent an exact mapping of the
. Essentially, the KS
equations represent an exact mapping of the  -electron problem
onto a set of
-electron problem
onto a set of 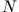 single-particle problems. The crucial point is,
however, that one does not know the KS potential explicitly.
Nevertheless, a few general properties of the KS potential can be
established: (i) the KS potential is local in space in contrast to
the exchange term in Hartree-Fock theory, (ii) by virtue of the
Runge-Gross theorem the KS potential
must be a unique functional of the exact density for a given
initial state
single-particle problems. The crucial point is,
however, that one does not know the KS potential explicitly.
Nevertheless, a few general properties of the KS potential can be
established: (i) the KS potential is local in space in contrast to
the exchange term in Hartree-Fock theory, (ii) by virtue of the
Runge-Gross theorem the KS potential
must be a unique functional of the exact density for a given
initial state 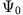 and for a given KS determinant
and for a given KS determinant
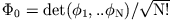 . The latter
condition can be largely simplified if we assume that the
time-dependent electronic system evolves from a
non-degenerate ground state of the initially undisturbed
system, which, via stationary DFT, is fully determined by its
corresponding density
. The latter
condition can be largely simplified if we assume that the
time-dependent electronic system evolves from a
non-degenerate ground state of the initially undisturbed
system, which, via stationary DFT, is fully determined by its
corresponding density 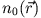 . In this case the KS potential
is a unique functional of the density alone
. In this case the KS potential
is a unique functional of the density alone
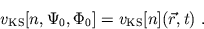 |
(10) |
Based on the experience with single-particle pictures one usually
splits the KS potential into its classical parts - the external
(Coulomb) interaction 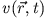 and the Hartree
potential
and the Hartree
potential
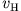 , which
includes the screening of the external potential due to the
electrons - and a genuine quantum part
, which
includes the screening of the external potential due to the
electrons - and a genuine quantum part
 the
exchange-correlation
potential
the
exchange-correlation
potential
However, as nothing is known about the exchange-correlation potential so
far, one needs an additional property of the many-particle system to
determine the KS potential explicitly.
The solution of the TDSE corresponds to a stationary point of the action
integral
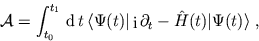 |
(12) |
which essentially should be a functional of 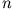 as
as  is. The TDSE
is then obtained by variation of
is. The TDSE
is then obtained by variation of 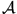 with respect to
with respect to  . Can
one therefore conclude that the exact one-particle density is a
stationary point of the action integral as well, thus
. Can
one therefore conclude that the exact one-particle density is a
stationary point of the action integral as well, thus
 ?
This is obviously not the case, as the Runge-Gross theorem
predicts the functional
?
This is obviously not the case, as the Runge-Gross theorem
predicts the functional 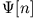 only up to an arbitrary time
phase. Because of the time-derivative in the Schrödinger
operator
only up to an arbitrary time
phase. Because of the time-derivative in the Schrödinger
operator
 the action (12) is, in
fact, a functional of
the action (12) is, in
fact, a functional of 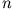 and the undetermined phase (for a
detailed discussion on appropriate action functionals see
[4] and [10]). Consequently, (12) is not
useful as an additional source for the derivation of the KS
potential.
A more pragmatic approach rests on the assumption that the
time-dependence of the KS potential is only due to the time-dependence
of the density, where the functional dependence on the density is taken
from stationary DFT. This is called the adiabatic
approximation. The exchange-correlation
(xc) potential for a nondegenerate
ground state is related to the corresponding energy on the basis of the
Rayleigh-Ritz variational principle
and the undetermined phase (for a
detailed discussion on appropriate action functionals see
[4] and [10]). Consequently, (12) is not
useful as an additional source for the derivation of the KS
potential.
A more pragmatic approach rests on the assumption that the
time-dependence of the KS potential is only due to the time-dependence
of the density, where the functional dependence on the density is taken
from stationary DFT. This is called the adiabatic
approximation. The exchange-correlation
(xc) potential for a nondegenerate
ground state is related to the corresponding energy on the basis of the
Rayleigh-Ritz variational principle
where 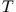 and
and 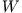 are the expectation values of the interacting
system,
are the expectation values of the interacting
system, 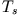 denotes the kinetic energy, and
denotes the kinetic energy, and  the
Hartree energy of the KS system. The functional derivative
(13) yields the functional dependence of the xc-potential
on
the
Hartree energy of the KS system. The functional derivative
(13) yields the functional dependence of the xc-potential
on 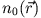 for any particular approximation of the energy
functional
for any particular approximation of the energy
functional
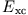 . Replacement of the ground-state
density by
. Replacement of the ground-state
density by 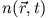 is the essential idea of the adiabatic
approximation.
is the essential idea of the adiabatic
approximation.
The Local-Density Approximation
The most convenient ansatz for the xc-energy is based on the
assumption that the energy functional can be locally approximated
by that of the homogeneous electron gas. This local-density approximation
(LDA) yields for the exchange
part a simple analytical expression
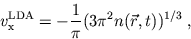 |
(14) |
while the correlation part is given in terms of a parametrization
[11]. The LDA (or ALDA for adiabatic LDA) should give
reasonable results for systems in which the density is slowly
varying both in space and time. However, it is important to note
that the exchange potential (14) decreases exponentially,
giving rise to an asymptotically incorrect compensation of the
self-energy contained in the Hartree term. In
atomic physics this can be cured by forcing the correct asymptotic
decrease of the KS potential [12].
The Optimized-Potential Method
The problems associated with the self-energy
effects can be solved more systematically on the basis of
orbital-dependent density functionals. As the KS orbitals are
also functionals of 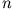 one can express the xc-potential as a
functional of the KS orbitals. Using the chain rule for functional
differentiation one obtains
one can express the xc-potential as a
functional of the KS orbitals. Using the chain rule for functional
differentiation one obtains
with cc indicating the complex conjugate of the preceding
expression. For the x-only term the exact energy functional is
known
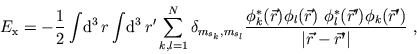 |
(16) |
which together with (15) yields an integral equation for
the local exchange part of the KS potential. This scheme,
originally introduced by Talman and Shadwick [13] as the
optimized (effective) potential method (OEP  OPM) has been shown to be very
successful in ground-state DFT
[14] as well as in time-dependent systems. The local
character of the x-potential allows for a compensation of the
self-energy not only for the occupied ground-state orbitals - as
is the case in Hartree-Fock theory - but also for the virtual
orbitals that is of particular interest in time-dependent systems.
The first attempts to include correlation [15] are very
promising for ground-state problems but are yet too complex for
time-dependent systems.
OPM) has been shown to be very
successful in ground-state DFT
[14] as well as in time-dependent systems. The local
character of the x-potential allows for a compensation of the
self-energy not only for the occupied ground-state orbitals - as
is the case in Hartree-Fock theory - but also for the virtual
orbitals that is of particular interest in time-dependent systems.
The first attempts to include correlation [15] are very
promising for ground-state problems but are yet too complex for
time-dependent systems.
H.J. Lüdde