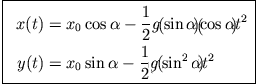Wir haben gesehen, dass die Gravitationskraft in Erdnähe nahezu konstant ist
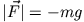 , so dass alle Massenpunkte die gleiche Beschleunigung
, so dass alle Massenpunkte die gleiche Beschleunigung
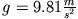 in Richtung zum Mittelpunkt der Erde erfahren.
Wir werden in Kapitel 6 sehen, dass diese Aussage kleiner Korrekturen bedarf,
weil insbesondere durch die Rotation der Erde der Globus elliptisch verformt ist.
Diese Korrekturen sind gering, so dass wir für den Moment annehmen können,
dass die reibungsfreie Bewegung aller Massen in Erdnähe durch die Wirkung
einer konstanten Kraft hervorgerufen wird.
in Richtung zum Mittelpunkt der Erde erfahren.
Wir werden in Kapitel 6 sehen, dass diese Aussage kleiner Korrekturen bedarf,
weil insbesondere durch die Rotation der Erde der Globus elliptisch verformt ist.
Diese Korrekturen sind gering, so dass wir für den Moment annehmen können,
dass die reibungsfreie Bewegung aller Massen in Erdnähe durch die Wirkung
einer konstanten Kraft hervorgerufen wird.
In diesem Fall lässt sich die Bewegungsgleichung
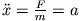 direkt integrieren. Da die Beschleunigung
direkt integrieren. Da die Beschleunigung 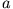 konstant ist gilt
konstant ist gilt
mit der Anfangsgeschwindigkeit
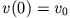 das Geschwindigkeits-Zeit-Gesetz
das Geschwindigkeits-Zeit-Gesetz
Das Weg-Zeit-Gesetz erhält man bei nochmaliger Integration über
die Zeit nach dem gleichen Schema
Bemerkungen
- (i)
- Jede Integration ergibt eine Integrationskonstante.
D.h.
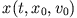 ist somit eine Lösungsschar,
abhängig von
ist somit eine Lösungsschar,
abhängig von 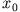 und
und 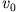 . Diese Lösungsschar stellt zunächst die
mathematisch allgemeine Lösung der Bewegungsgleichung
(oder allgemeiner einer Differentialgleichung 2. Ordnung) dar.
. Diese Lösungsschar stellt zunächst die
mathematisch allgemeine Lösung der Bewegungsgleichung
(oder allgemeiner einer Differentialgleichung 2. Ordnung) dar.
- (ii)
- Jede spezielle physikalische Situation erfordert die Festlegung der
Integrationskonstanten durch die Anfangsbedingungen
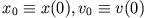 der Bewegung.
der Bewegung.
Beispiele
Die Beispiele werden zeigen, dass wir mit der selben allgemeinen Lösung ganz unterschiedliche
Bewegungsformen im erdnahen Gravitationsfeld beschreiben können.
B2.1 Freier Fall ohne Reibung
Abbildung 2.1:
Stroboskopansicht für den freien Fall
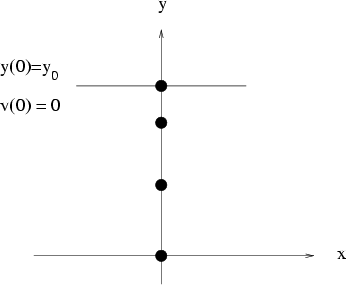 |
Abbildung 2.1 zeigt Stroboskopaufnahmen eines Massenpunktes, der aus der Höhe 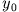 und aus der Ruhe unter dem Einfluss der Gravitation reibungsfrei zu Boden
und aus der Ruhe unter dem Einfluss der Gravitation reibungsfrei zu Boden 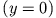 fällt.
In gleichen Zeiteinheiten (Stroboskopintervallen) legt der Massenpunkt immer größere
Strecken zurück.
Aus (2.1), (2.2) erhalten wir für die speziellen Anfangsbedingungen
fällt.
In gleichen Zeiteinheiten (Stroboskopintervallen) legt der Massenpunkt immer größere
Strecken zurück.
Aus (2.1), (2.2) erhalten wir für die speziellen Anfangsbedingungen
Daraus lassen sich z. B. die Auftreffzeit 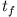
und die Auftreffgeschwindigkeit
berechnen.
B2.2 Waagrechter Wurf ohne Reibung
Abbildung 2.2:
Waagrechter Wurf
 |
Warum ist das offensichtlich zweidimensionale Wurfproblem eigentlich doch nur
eindimensional ? Im ersten Schritt der eingangs erwähnten ''Analyse-Rezeptur''
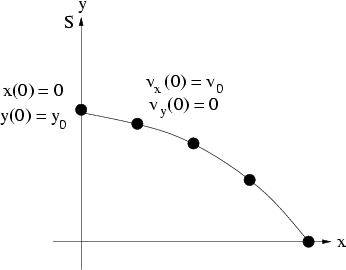
wählen wir ein Inertialsystem, das sich mit der Geschwindigkeit 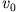 relativ zu
relativ zu 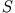 bewegt
und betrachten relativ zu diesem bewegten Bezugssystem
bewegt
und betrachten relativ zu diesem bewegten Bezugssystem 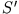 das Wurfproblem:
der Massenpunkt bewegt sich offenbar entlang der neuen
das Wurfproblem:
der Massenpunkt bewegt sich offenbar entlang der neuen 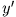 -Achse in freien Fall.
-Achse in freien Fall.
Abbildung 2.3:
Der waagrechte Wurf in 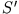 erscheint als freier Fall.
erscheint als freier Fall.
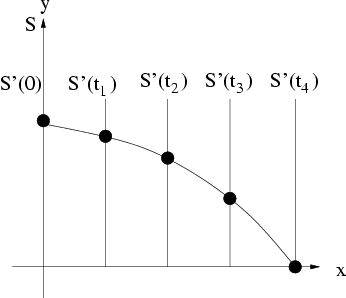 |
D. h. wir können den waagrechten Wurf durch eine geschickte Wahl des Bezugssystems auf den freien Fall
zurückführen.
Mathematisch ist der Zusammenhang zwischen  und
und 
In  beobachtet man einen freien Fall
beobachtet man einen freien Fall
und in 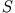 den waagrechten Wurf
den waagrechten Wurf
Kontrollfrage:
Eine Gewehrkugel wird aus der Höhe 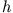 waagrecht
abgeschossen. Gleichzeitig lässt man ein schweres Bleigewicht aus derselben Höhe
frei fallen. Beide Objekte bewegen sich reibungsfrei.
Welches Objekt berührt zuerst den Boden ?
waagrecht
abgeschossen. Gleichzeitig lässt man ein schweres Bleigewicht aus derselben Höhe
frei fallen. Beide Objekte bewegen sich reibungsfrei.
Welches Objekt berührt zuerst den Boden ?
A)die Gewehrkugel
B)das Bleigewicht
C)beide Objekte berühren gleichzeitig den Boden
D)weiß nicht .
B2.3 Schiefe Ebene
Abbildung 2.4:
Gleitende Bewegung entlang einer schiefen Ebene.
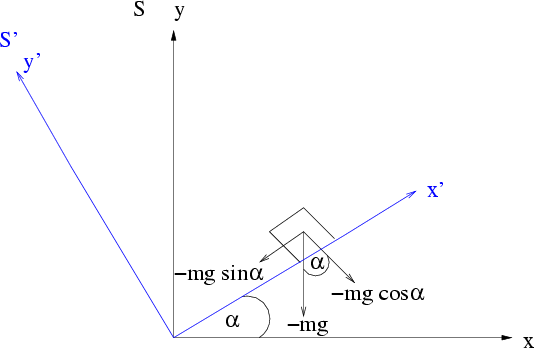 |
Eine Masse 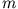 rutscht reibungsfrei entlang einer schiefen Ebene. Entsprechend
unserem ''Rezept'' suchen wir zunächst nach der Kraft, die diese Bewegung verursacht.
Die Kraftkomponente der Schwerkraft senkrecht zur Ebene wird von den Materialkräften
innerhalb der Ebene kompensiert. (Man nennt solche Kräfte Zwangskräfte. Sie sorgen
dafür, dass der Massenpunkt die Ebene nicht verlassen kann, tragen aber nicht zur
Bewegung bei.)
Es bleibt die Kraftkomponente parallel zur Ebene (Hangabtriebskraft),
die die Masse aus der Ruhe
rutscht reibungsfrei entlang einer schiefen Ebene. Entsprechend
unserem ''Rezept'' suchen wir zunächst nach der Kraft, die diese Bewegung verursacht.
Die Kraftkomponente der Schwerkraft senkrecht zur Ebene wird von den Materialkräften
innerhalb der Ebene kompensiert. (Man nennt solche Kräfte Zwangskräfte. Sie sorgen
dafür, dass der Massenpunkt die Ebene nicht verlassen kann, tragen aber nicht zur
Bewegung bei.)
Es bleibt die Kraftkomponente parallel zur Ebene (Hangabtriebskraft),
die die Masse aus der Ruhe
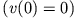 bewegt. Ferner erscheint uns die Bewegung eindimensional wenn
wir sie im Bezugssystem
bewegt. Ferner erscheint uns die Bewegung eindimensional wenn
wir sie im Bezugssystem 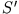 betrachten.
Somit erhält man aus (2.2) für die Bewegung in
betrachten.
Somit erhält man aus (2.2) für die Bewegung in 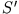
Der Zusammenhang zwischen 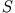 und
und 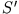 ist (für
ist (für 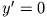 )
)
Damit erhält man für die Bewegung in 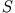 Als Extremfälle betrachten wir
Als Extremfälle betrachten wir
U. Lechner, H.J. Lüdde
![]() , so dass alle Massenpunkte die gleiche Beschleunigung
, so dass alle Massenpunkte die gleiche Beschleunigung
![]() in Richtung zum Mittelpunkt der Erde erfahren.
Wir werden in Kapitel 6 sehen, dass diese Aussage kleiner Korrekturen bedarf,
weil insbesondere durch die Rotation der Erde der Globus elliptisch verformt ist.
Diese Korrekturen sind gering, so dass wir für den Moment annehmen können,
dass die reibungsfreie Bewegung aller Massen in Erdnähe durch die Wirkung
einer konstanten Kraft hervorgerufen wird.
in Richtung zum Mittelpunkt der Erde erfahren.
Wir werden in Kapitel 6 sehen, dass diese Aussage kleiner Korrekturen bedarf,
weil insbesondere durch die Rotation der Erde der Globus elliptisch verformt ist.
Diese Korrekturen sind gering, so dass wir für den Moment annehmen können,
dass die reibungsfreie Bewegung aller Massen in Erdnähe durch die Wirkung
einer konstanten Kraft hervorgerufen wird.
![]() direkt integrieren. Da die Beschleunigung
direkt integrieren. Da die Beschleunigung ![]() konstant ist gilt
konstant ist gilt
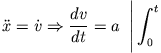
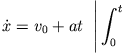
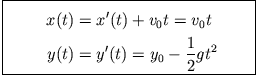
![]() waagrecht
abgeschossen. Gleichzeitig lässt man ein schweres Bleigewicht aus derselben Höhe
frei fallen. Beide Objekte bewegen sich reibungsfrei.
Welches Objekt berührt zuerst den Boden ?
waagrecht
abgeschossen. Gleichzeitig lässt man ein schweres Bleigewicht aus derselben Höhe
frei fallen. Beide Objekte bewegen sich reibungsfrei.
Welches Objekt berührt zuerst den Boden ?
![]() rutscht reibungsfrei entlang einer schiefen Ebene. Entsprechend
unserem ''Rezept'' suchen wir zunächst nach der Kraft, die diese Bewegung verursacht.
Die Kraftkomponente der Schwerkraft senkrecht zur Ebene wird von den Materialkräften
innerhalb der Ebene kompensiert. (Man nennt solche Kräfte Zwangskräfte. Sie sorgen
dafür, dass der Massenpunkt die Ebene nicht verlassen kann, tragen aber nicht zur
Bewegung bei.)
Es bleibt die Kraftkomponente parallel zur Ebene (Hangabtriebskraft),
die die Masse aus der Ruhe
rutscht reibungsfrei entlang einer schiefen Ebene. Entsprechend
unserem ''Rezept'' suchen wir zunächst nach der Kraft, die diese Bewegung verursacht.
Die Kraftkomponente der Schwerkraft senkrecht zur Ebene wird von den Materialkräften
innerhalb der Ebene kompensiert. (Man nennt solche Kräfte Zwangskräfte. Sie sorgen
dafür, dass der Massenpunkt die Ebene nicht verlassen kann, tragen aber nicht zur
Bewegung bei.)
Es bleibt die Kraftkomponente parallel zur Ebene (Hangabtriebskraft),
die die Masse aus der Ruhe
![]() bewegt. Ferner erscheint uns die Bewegung eindimensional wenn
wir sie im Bezugssystem
bewegt. Ferner erscheint uns die Bewegung eindimensional wenn
wir sie im Bezugssystem ![]() betrachten.
Somit erhält man aus (2.2) für die Bewegung in
betrachten.
Somit erhält man aus (2.2) für die Bewegung in ![]()