Das Foucaultsche Pendel
Das Projekt Foucaultsche Pendel ist ein Anwendungsfall der Newtonschen Mechanik in bewegten Bezugssystemen (siehe untere Animation). Das System besteht aus einem Pendel, welches sich auf der rotierenden Erde befindet und sich deshalb in einem rotierenden Koordinatensystem befindet (Luftreibung wird im Folgenden vernachlässigen). Betrachtet man sich die Bewegung eines Körpers (beschrieben durch $\vec{r}(t)$) in einem mit der Winkelgeschwindigkeit $\vec{\omega}$ rotierenden Koordinatensystem, so treten aufgrund der Rotation zusätzliche Komponenten in den Grundgleichungen der Mechanik auf. Die Gleichungen der Mechanik eines Körpers der Masse $m$ auf den eine Kraft $\vec{F}$ in einem rotierenden Bezugssystem einwirkt, lauten (siehe Walter Greiner, 'Klassische Mechanik II' [8. Auflage, 2008, Kapitel I1. Seite 5]): $$ \begin{equation} m \frac{d^2 \vec{r}}{dt^2} = \vec{F} - \underbrace{m \, \frac{d \vec{\omega}}{dt} \times \vec{r}}_{\hbox{lineare Beschleunigung}} - \underbrace{2m \, \vec{\omega} \times \vec{v}}_{\hbox{Coriolisbeschleunigung}} - \underbrace{m \, \vec{\omega} \times \left( \vec{\omega} \times \vec{r} \right)}_{\hbox{Zentripedalbeschleunigung}} \end{equation} $$
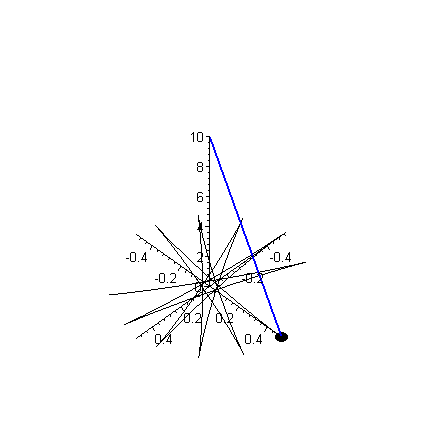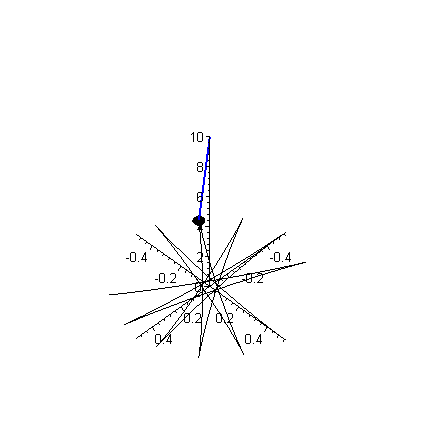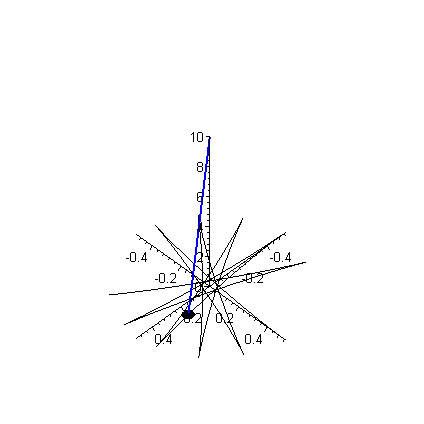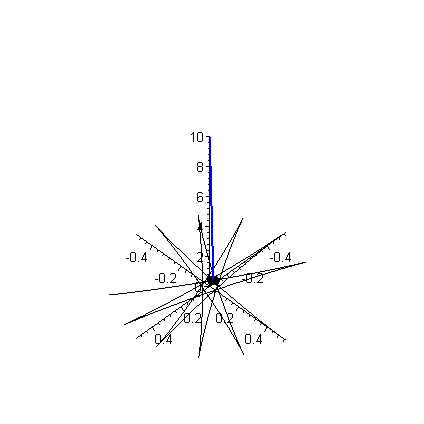
Da sich das Foucaultsche Pendel auf der Erde befindet, und diese ja weitgehendst mit konstanter Winkelgeschwindigkeit rotiert ($\frac{d \vec{\omega}}{dr} \approx 0$), kann man den Term der die 'lineare Beschleunigung' aufgrund der Erdrotation beschreibt vernachlässigen. Auch ist die Winkelgeschwindigkeit der Erde klein gegenüber der Schwingungsdauer des Pendels, sodass der Term der 'Zentripedalbeschleunigung' ebenfalls klein ist, da dieser $\sim \omega^2$ geht. Die auf den Pendelkörper einwirkende Kraft besteht aus der Zugkraft $\vec{T}$ des Pendelfadens und der nach unten gerichteten Gravitationskraft ($\vec{F} = \vec{T} + m\vec{g}$). Man erhält somit in Näherung $$ \begin{equation} m \frac{d^2 \vec{r}}{dt^2} = \vec{T} + m\vec{g} - 2m \, \vec{\omega} \times \vec{v} \quad . \end{equation} $$ Aufgrund des Terms der 'Coriolisbeschleunigung' ist die obere Gleichung ein gekoppeltes System von drei Differentialgleichungen zweiter Ordnung, welches man zunächst in ein System aus sechs Differentailgleichungen erster Ordnung umschreiben muss, um es numerisch lösen zu können.
Mögliche Teilaufgaben des Projektes
Schreiben Sie zunächst die Bewegungsgleichung in ein System von erster Ordnung Differentialgleichungen um (gerne mittels Python-Jupyter + SymPy).
Lösen Sie das System aus sechs Differentialgleichungen erster Ordnung mittels eines C++ Programms und benutzen Sie das Runge-Kutta Ordnung vier Verfahren.
Betrachten Sie unterschiedliche Anfangsbedingungen und visualisieren Sie ihre Ergebnisse mittels eines Python Skriptes bzw. Jupyter Notebooks.
Die Bewegung des Foucaultschen Pendels hängt davon ab, an welcher Stelle man sich auf der Erde befindet. Zeigen Sie dies mittels einer numerischen Simulation.
Vernachlässigen Sie nun nicht mehr die Terme der 'lineare Beschleunigung' und 'Zentripedalbeschleunigung' und nehmen eine große und sich zeitlich verändernde Winkelgeschwindigkeit des rotierenden Koordinatensystems an. Wie schnell muss das System rotieren, dass die Terme nicht mehr zu vernachlässigen sind.
Wie würde die Bewegung des Pendels auf dem Mond oder auf einem Neutronenstern aussehen?
Schreiben Sie Ihr Programm so um, dass das Foucaultsche Pendel eine Klasse (mit eigenen Daten-Member, Member Funktionen und Konstruktoren) repräsentiert.
Weitere Links