Differentialgleichungen: Numerische Lösung von Anfangswertproblemen
Im vorigen Unterpunkt hatten wir die Bewegung einzelner Teilchen in einer Kiste simuliert. In der Physik ist die zeitliche Entwicklung eines Systems of in Form von Differentialgleichungen (DGLs) gegeben. In diesem Unterpunkt betrachten wir das numerische Lösen einer Differentialgleichung erster Ordnung der Form $$ \begin{equation} \dot{y}(t) = \frac{d y(t)}{dt} = f(t,y(t)) \quad, \, \hbox{mit:} \,\, a \leq t \leq b \, , \,\, y(a)=\alpha \quad. \end{equation} $$ Die Funktion $f(t,y(t))$ bestimmt die DGL und somit das Verhalten der gesuchten Funktion $y(t)$. Es wird hierbei vorausgesetzt, dass $f(t,y(t))$ auf einer Teilmenge ${\cal D}=\{ (t,y) | a \leq t \leq b \, , \,\, -\infty \leq y \leq \infty \}$ kontinuierlich definiert ist. Weiter wird angenommen, dass das so definierte Anfangswertproblem "well-posed" ist und eine eindeutige Lösung $y(t)$ existiert ("well-posed" bedeutet hier, dass die Differentialgleichung eine Struktur hat, bei der kleine Störungen im Anfangszustand nicht exponentiell anwachsen). Wir hatten bereits gesehen, wie man Differentialgleichungen mittels Jupyter Notebooks und SymPy DGLs analytisch löst (siehe Jupyter Notebooks und das Rechnen mit symbolischen Ausdrücken). Nicht jede DGL lässt sich analytisch lösen und falls der Befehl "dsolve()" keine sinnvollen Resultate liefert, muss man die zeitliche Entwicklung der Funktion $y(t)$ numerisch berechnen. Die numerische Lösung der DGL kann man sich auch direkt in Python mittels der Methode "integrate.odeint()" berechnen (Python-Modul "scipy" ). Möchte man die Lösung jedoch in einem C++ Programm berechnen, so ist man auf die Anwendung eines numerischen Verfahrens angewiesen.
Das einfache Euler Verfahren zum Lösen einer DGL
Das wohl einfachste Verfahren zum Lösen einer DGL erster Ordnung ist die Euler Methode. Hierzu schreibt man die DGL als eine Differenzengleichung um $$ \begin{equation} \frac{d y(t)}{dt} = f(t,y(t)) \,\, \rightarrow \,\, \Delta y = f(t,y) \cdot \Delta t \,\, \rightarrow \,\, \Delta y = h \cdot f(t,y) \end{equation} $$ und unterteilt das Zeitintervall $[a,b]$ in $N+1$ äquidistante Zeit-Gitterpunkte $\left( t_0, t_1, t_2, ..., t_N \right) $, wobei $t_i = a + i \, h \quad \forall i=0,1,2,...,N$. Im Algorithmus der Euler Methode startet man bei $t=t_0$ und $y=y_0=\alpha$ (Anfangsbedingungen des Systems) und erhöht dann iterativ die Zeit $t$ um den Wert von $h$. Den neuen y-Wert erhält man mittels $y_1 = y_0 + h \cdot f(t_0,y_0)$ und man führt das Verfahren so lange aus, bis man an den letzten zeitlichen Gitterpunkt gelangt.
Betrachten wir z.B. die einfache Differentialgleichung $$ \begin{equation} \frac{d y(t)}{dt} = f(t,y(t)) = - y(t) \quad , \end{equation} $$ die den exponentiellen Abfall einer Funktion $y(t)$ beschreibt. Obwohl sich die allgemeine Lösung der DGL einfach bestimmen lässt ($y(t)= \alpha \cdot e^{-t}$, mit $\alpha=y(0)$), möchten wir die DGL auf numerischem Wege lösen. Das folgende C++ Programm benutzt die Eulermethode und entwickelt die obere Differentialgleichung im Zeitintervall $[a,b]=[0,2]$ mittels 101 Gitterpunkten. Die simulierten Daten werden dann, zusammen mit der analytischen Lösung im Terminal ausgegeben.
/* Berechnung der Lösung einer Differentialgleichung der Form y'=f(t,y) * mittels der einfachen Euler Methode und f(t,y) = y * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double t, double y){ // Definition der Funktion f(t,x) double wert; wert = - y; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(t,x) } // Ende der Funktion f(t,x) double y_analytisch(double t, double alpha){ // Analytische Loesung der DGL double wert; // bei gegebenem Anfangswert y(a)=alpha wert = alpha*exp(-t); // Eigentliche Definition der analytische Loesung return wert; // Rueckgabewert } // Ende der Definitiom int main(){ // Hauptfunktion double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 2; // Obergrenze des Intervalls [a,b] int N = 100; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha = 0.5; // Anfangswert bei t=a: y(a)=alpha double t; // Aktueller Zeitwert double y = alpha; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode printf("# 0: Index i \n# 1: t-Wert \n# 2: Euler Methode \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Analytische Loesung \n"); // Beschreibung der ausgegebenen Groessen for(int i = 0; i <= N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls t = a + i*h; // Zeit-Parameter wird um h erhoeht printf("%3d %19.15f %19.15f %19.15f\n",i, t, y, y_analytisch(t,0.5)); // Ausgaben der Loesung y = y + h*f(t,y); // Euler Methode } // Ende for-Schleife } // Ende der Hauptfunktion
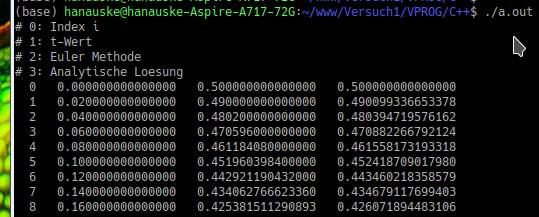
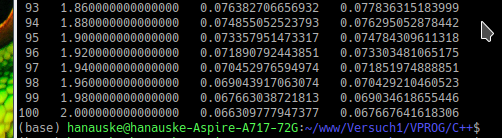
Die oberen beiden Abbildungen zeigen die ersten und letzten ausgegebenen Werte des Programms. Man erkennt, dass die Abweichungen zum wirklichen Wert, am Anfang der Simulation noch recht klein sind. Im Laufe der Simulation kumulieren sich jedoch die einzelnen Fehler der vorausgegangenen Berechnungen und der Fehler wird größer. In der numerischen Mathematik gibt es weit bessere Verfahren als die dargestellte einfache Euler Methode. Im Folgenden sollen einige dieser Verfahren zur Lösung einer DGL kurz vorgestellt werden.
Numerische Verfahren zum Lösen von Differentialgleichung erster Ordnung
In der numerischen Mathematik werden, mittels des Taylorschen Satzes für zwei Variablen, mehrere Methoden zur approximativen Lösung einer DGL hergeleitet. Die Herleitung dieser Verfahren soll hier nicht näher betrachtet werden, aber ähnlich wie bei den Regeln der Differentiation und Integration werden bei den Regeln unterschiedlich viele Stützstellenpunkte bei der Ermittlung des nächsten iterativen Zeitschrittes benutzt. Einige der Verfahren sind in der folgenden Box aufgelistet.
Anwendung auf die DGL: $\frac{d y}{dt} = y - t^2 + 1$
In dem folgenden C++ Programm wurde die Differentialgleichung $\frac{d y}{dt} = y - t^2 + 1$ in den Grenzen $t \in [a,b]=[0,2]$ mittels unterschiedlicher Lösungsmethoden zeitlich entwickelt. Es wurden hierbei lediglich 11 Gitterpunkte verwendet und zum Vergleich wurden die unterschiedlichen Approximierungsverfahren mit dem analytischen Wert verglichen und im Terminal ausgegeben.
/* Berechnung der Lösung einer Differentialgleichung der Form y'=f(t,y) * mittels unterschiedlich Verfahren * (einfache Euler Methode, Midpoint, Modified Euler und Runge-Kutta Ordnung vier) * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Ausgabe zum Plotten mittels Python Jupyter Notebook DGL_1.ipynb: "./a.out > DGL_1.dat */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double t, double y){ // Definition der Funktion f(t,x) double wert; wert = y - pow(t,2) +1; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(t,x) } // Ende der Funktion f(t,x) double y_analytisch(double t, double alpha){ // Analytische Loesung der DGL double wert; // bei gegebenem Anfangswert y(a)=alpha wert = (alpha + (pow(t,2) + 2*t + 1)*exp(-t) -1)*exp(t); // Eigentliche Definition der analytische Loesung return wert; // Rueckgabewert } // Ende der Definitiom int main(){ // Hauptfunktion double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 2; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha = 0.5; // Anfangswert bei t=a: y(a)=alpha double t; // Aktueller Zeitwert double y_Euler = alpha; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode double y_Midpoint = alpha; // Deklaration und Initialisierung der numerischen Loesung der Mittelpunkt Methode double y_Euler_M = alpha; // Deklaration und Initialisierung der numerischen Loesung der modifizierte Euler Methode double y_RungeK_4 = alpha; // Deklaration und Initialisierung der numerischen Loesung der Runge-Kutta Ordnung vier Methode double k1, k2, k3, k4; // Deklaration der vier Runge-Kutta Parameter printf("# 0: Index i \n# 1: t-Wert \n# 2: Euler Methode \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: Mittelpunkt Methode \n# 4: Modifizierte Euler Methode \n"); // Beschreibung der ausgegebenen Groessen printf("# 5: Runge-Kutta Ordnung vier \n# 6: Analytische Loesung \n"); // Beschreibung der ausgegebenen Groessen for(int i = 0; i <= N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls t = a + i*h; // Zeit-Parameter wird um h erhoeht printf("%3d %19.15f %19.15f %19.15f %19.15f %19.15f %19.15f\n",i, t, y_Euler, y_Midpoint, y_Euler_M, y_RungeK_4, y_analytisch(t,0.5)); // Ausgaben der Loesung y_Euler = y_Euler + h*f(t,y_Euler); // Euler Methode y_Midpoint = y_Midpoint + h*f(t+h/2,y_Midpoint+h/2*f(t,y_Midpoint)); // Mittelpunkt Methode y_Euler_M = y_Euler_M + h/2*( f(t,y_Euler_M) + f(t+h,y_Euler_M+h*f(t,y_Euler_M)) ); // Modifizierte Euler Methode k1 = h*f(t,y_RungeK_4); // Runge-Kutta Parameter 1 k2 = h*f(t+h/2,y_RungeK_4+k1/2); // Runge-Kutta Parameter 2 k3 = h*f(t+h/2,y_RungeK_4+k2/2); // Runge-Kutta Parameter 3 k4 = h*f(t+h,y_RungeK_4+k3); // Runge-Kutta Parameter 4 y_RungeK_4 = y_RungeK_4 + (k1 + 2*k2 + 2*k3 + k4)/6; // Runge-Kutta Ordnung vier Methode } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls } // Ende der Hauptfunktion
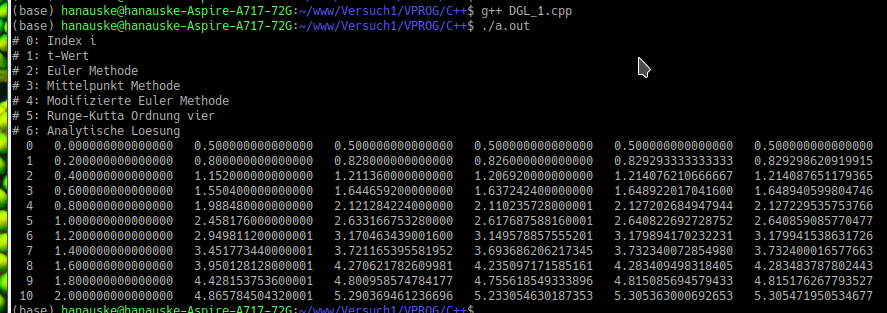
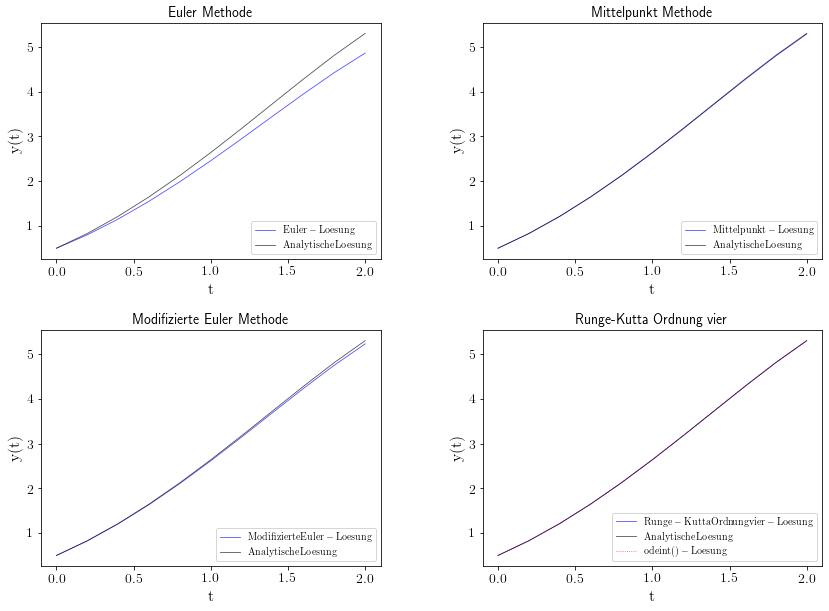
Die obere linke Abbildung veranschaulicht die Terminalausgabe des Programms. Man erkennt wieder, dass die berechneten approximativen Werte für alle Verfahren am Anfang gut mit dem wirklichen Wert übereinstimmen, je mehr man jedoch gegen Ende der Simulation kommt, desto größer wird der Fehler. Die Fehler der einzelnen Verfahren unterscheiden sich jedoch erheblich voneinander und sind kleiner, je höher die Ordnung $N$ der Methode ist.
Beim Klicken auf das obere rechte Bild gelangen Sie zu dem Jupyter Notebook DGL_1.ipynb in dem eine Visualisierung der Ergebnisse des C++ Programms programmiert ist. Die untere Abbildung zeigt z.B. die Visualisierung der Daten von DGL_1.cpp. Zusätzlich wird in dem Notebook auch die numerische Lösung direkt in Python generiert (Methode "integrate.odeint()" im Python-Modul "scipy") und mit den simulierten Daten der unterschiedlichen Verfahren verglichen.
